95. 不同的二叉搜索树 II

news2024/11/24 1:15:57

95. 不同的二叉搜索树 II

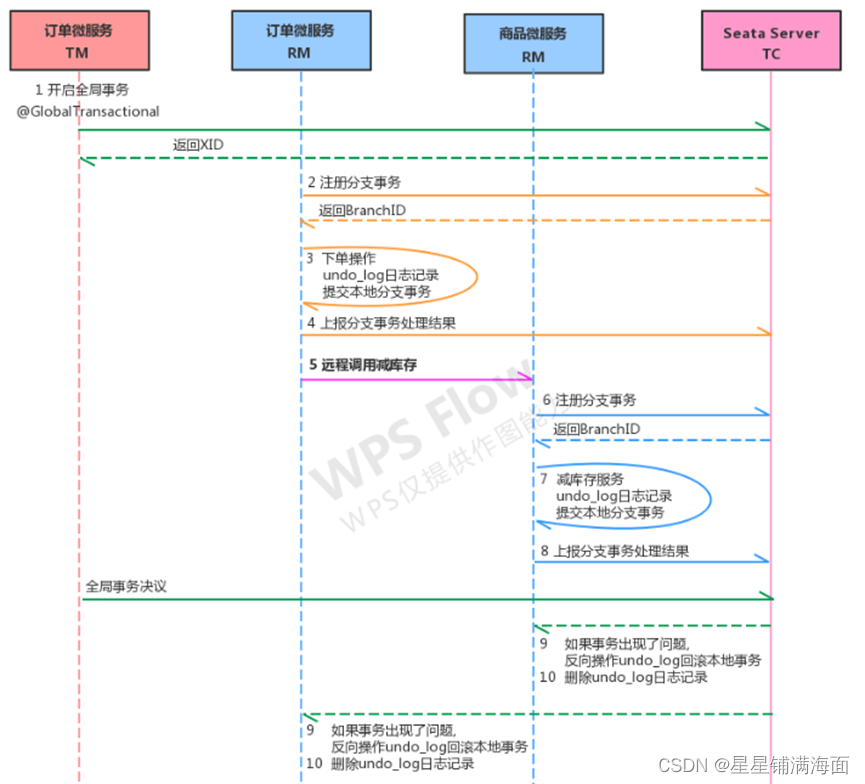
题目
算法设计：深度优先搜索

题目

传送门：https://leetcode.cn/problems/unique-binary-search-trees-ii/

算法设计：深度优先搜索

二叉树子问题分解 = 根节点 + 左右子树的子问题。

根节点的子问题：循环历遍每一个元素，以这个元素作为根节点。

左子树的子问题：左子树的所有可行的集合。

右子树的子问题：右子树的所有可行的集合。

分析过程：

二叉搜索树关键的性质是，根节点的值大于左子树所有节点的值，小于右子树所有节点的值，且左子树和右子树也同样为二叉搜索树。
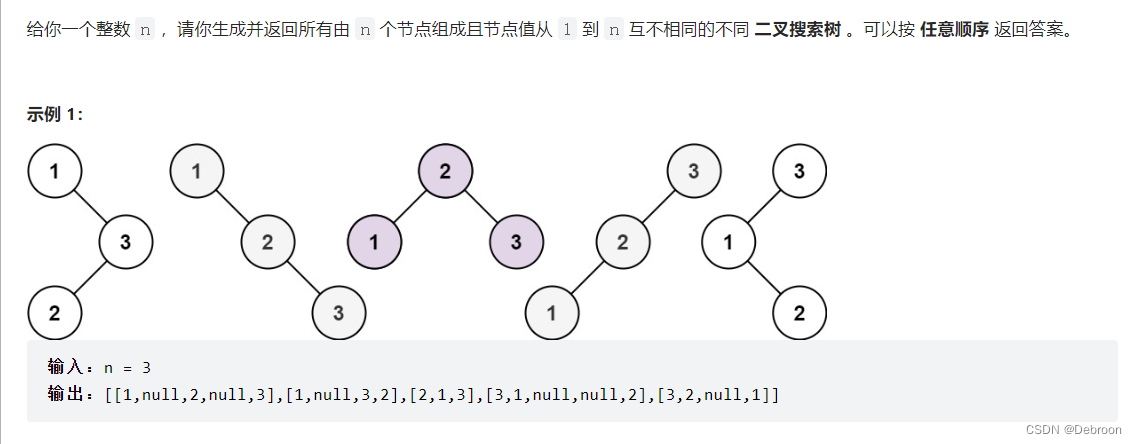
题目数据 [1, n] 是一个单调递增序列。
那以 i 作为根节点，那比它小的元素 [1, i-1] 就只能是属于它的左子树，比它大的节点 [i+1, n]只能是属于它的右子树。
比如 $n = 5 ， i = 3$ ，根据二叉搜索树性质，左子树节点就是 {1,2} 的组合，右子树就是 {4,5} 的组合。
以 3 为根节点的二叉搜索树数量 = 左子树的所有可行的集合 * 右子树的所有可行的集合。
n 的所有二叉搜索树数量 = 以 1 为根节点的二叉搜索树数量 + 以 2 为根节点的二叉搜索树数量 + 以 3 为根节点的二叉搜索树数量 + 以 4 为根节点的二叉搜索树数量 + 以 5 为根节点的二叉搜索树数量

class Solution {
public:
    vector<TreeNode*> dfs(int start, int end) {
        vector<TreeNode*> res;
        if (start > end) return {NULL};                    // 空树
        for (int i = start; i <= end; i++) {               // 枚举每个 i 为根节点
            vector<TreeNode*> left = dfs(start, i-1), right = dfs(i+1, end);  
            // 以i作为根节点，那比它小的元素[1, i-1]就只能是它的左子树，比它大的节点[i+1, n]只能是它的右子树。再递归调用，得出所有可行的左子树和可行的右子树。
            for (auto l : left)                            // 从可行左子树集合中选一棵
                for (auto r : right)                       // 从可行右子树集合中选一棵
                    res.push_back(new TreeNode(i, l, r));  // 并拼接到根节点i上，把生成的子树序列放入答案数组
        }
        return res;                                        // 再由子树的解推出原问题的解
    }
    
    vector<TreeNode*> generateTrees(int n) {
        vector<TreeNode*> res = dfs(1, n);
        return res;
    }
};