秋名山码民的主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
🙏作者水平有限，如发现错误，还请私信或者评论区留言！

---

前言

线段树算是比较难的一个数据结构，当时我高中提高组就没学懂，细数我学线段树也学了4遍，最早学的时候一脸懵逼，最近在刷题中发现其在蓝桥杯中也有考察，就寻思写一篇博客来巩固。

什么是线段树，线段树有什么用，线段树怎么写，能不能背过？？？

我认为对于打比赛的各位来说，线段树和前缀和一样，不能算做算法，它更多的是一种工具，一种时间复杂度为O(logn)的单点修改，区间查询的工具

线段树逻辑概念

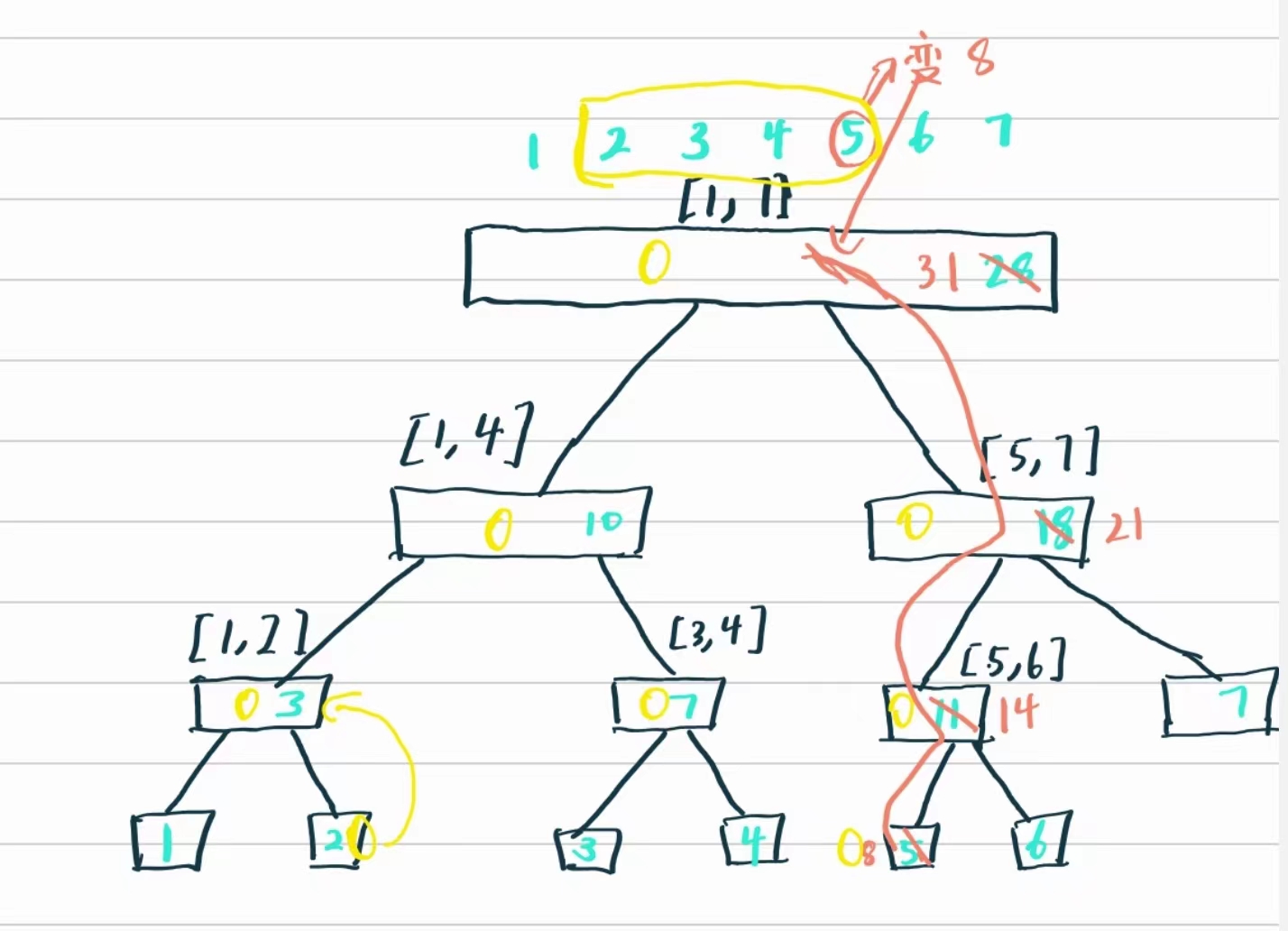
给定一个1~7的区间我们来维护它，将其转换为一个二叉树（线段树本身就是一个二叉树）

1. 最上面的根的权值，为28，1~7的和
2. 二叉树开分，左边为1~4的和为10，右边为5 ~ 6的和为21
3. 1~4在开分，左边为3，右边为7 ，5 ~6开分，左边为14，右边为7
4. 同上，直到不能再分

L，R：

class node{
    int l,r;
    int sum;
}

线段树的俩个重要用处

1. 单点修改

如上图我们将5变成8，其中要修改的为1~ 7，5~ 7，5~ 6，5，

2. 区间查询

如上图我们计算2 ~ 5区间，如果完全包含某个区间，则退出，否则进行递归，用黄圈表示需要递归的区间

1. 1~7区间，递归左边，1 ~4区间，发现还没有被完全包含，进行左右俩边都递归，1 ~2，3 ~4，此刻，3 ~4完全包含，不进行递归，继续递归1~ 2，2被完全包含
2. 5~ 7区间，同上，进行递归
3. 进行回溯区间，只算完全包含的区间，2+7+8 = 17

总结：
如果这个区间被完全包括在目标区间里面，直接返回这个区间的值
如果这个区间的左儿子和目标区间有交集，那么搜索左儿子
如果这个区间的右儿子和目标区间有交集，那么搜索右儿子

时间复杂度均为O(logn)

代码实现线段树

上面我们说线段树的俩个重要的用法，思考一下大概需要几个函数能实现？

1. pushup：用子节点信息更新当前节点信息
2. build：在一段区间上初始化线段树
3. modify：修改
4. query：查询

动态求连续区间和

import java.io.*;

/**
 * @Author 秋名山码神
 * @Date 2023/2/9
 * @Description
 */
public class 动态求连续区间和 {
    static int n, k;
    static int[] a = new int[100100];
    static Node[] tr = new Node[400400];
    static class Node{
        int l, r, sum;
        Node(int l, int r, int sum) {
            this.l = l;
            this.r = r;
            this.sum = sum;
        }
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        String[] cd = br.readLine().split(" ");
        n = Integer.parseInt(cd[0]);
        k = Integer.parseInt(cd[1]);

        String[] line = br.readLine().split(" ");
        for (int i=1;i<=n;i++)
            a[i] = Integer.parseInt(line[i-1]);

        build(1, 1, n);

        while (k-- > 0) {
            String[] li = br.readLine().split(" ");
            int k = Integer.parseInt(li[0]), l = Integer.parseInt(li[1]), r = Integer.parseInt(li[2]);
            if(k == 0) {
                bw.write(String.valueOf(query(1, l, r)));
                bw.write("\n");
            } else
                modify(1, l, r);
        }
        bw.flush();
    }
    static void pushUp(int u) {
        tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
    }

    static void build(int u, int l, int r) {
        if(l == r) tr[u] = new Node(l , r, a[l]);
        else {
            tr[u] = new Node(l ,r, 0);
            int mid = l + r >> 1;
            build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);
            pushUp(u);
        }
    }

    static int query(int u, int l, int r) {
        if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
        int mid = tr[u].l + tr[u].r >> 1, sum = 0;
        if(l <= mid) sum += query(u << 1, l, r);
        if(r > mid) sum += query(u << 1 | 1, l , r);
        return sum;
    }

    static void modify(int u, int x, int v) {
        if(tr[u].l == tr[u].r) tr[u].sum += v;
        else {
            int mid = tr[u].l + tr[u].r >> 1;
            if(x <= mid) modify(u << 1, x , v);
            else modify(u << 1 | 1, x, v);
            pushUp(u);
        }
    }
}

题目巩固

区间和的个数

class Solution {
    public int countRangeSum(int[] nums, int lower, int upper) {
        int count = 0;
        int length = nums.length;
        long[] sums = new long[length + 1];
        for (int i = 0; i < length; i++) {
            sums[i + 1] = sums[i] + nums[i];
        }
        Set<Long> set = new HashSet<Long>();
        for (int i = 0; i <= length; i++) {
            long sum = sums[i];
            set.add(sum);
            set.add(sum - upper);
            set.add(sum - lower);
        }
        List<Long> sumsList = new ArrayList<Long>(set);
        Collections.sort(sumsList);
        Map<Long, Integer> ranks = new HashMap<Long, Integer>();
        int size = sumsList.size();
        for (int i = 0; i < size; i++) {
            ranks.put(sumsList.get(i), i);
        }
        SegmentTree st = new SegmentTree(size);
        for (int i = 0; i <= length; i++) {
            long sum = sums[i];
            int rank = ranks.get(sum);
            long minSum = sum - upper, maxSum = sum - lower;
            int start = ranks.get(minSum), end = ranks.get(maxSum);
            count += st.getCount(start, end);
            st.add(rank);
        }
        return count;
    }
}

class SegmentTree {
    int length;
    int[] tree;

    public SegmentTree(int length) {
        this.length = length;
        this.tree = new int[length * 4];
    }

    public int getCount(int start, int end) {
        return getCount(start, end, 0, 0, length - 1);
    }

    public void add(int rank) {
        add(rank, 0, 0, length - 1);
    }

    private int getCount(int rangeStart, int rangeEnd, int index, int treeStart, int treeEnd) {
        if (rangeStart > rangeEnd) {
            return 0;
        }
        if (rangeStart == treeStart && rangeEnd == treeEnd) {
            return tree[index];
        }
        int mid = treeStart + (treeEnd - treeStart) / 2;
        if (rangeEnd <= mid) {
            return getCount(rangeStart, rangeEnd, index * 2 + 1, treeStart, mid);
        } else if (rangeStart > mid) {
            return getCount(rangeStart, rangeEnd, index * 2 + 2, mid + 1, treeEnd);
        } else {
            return getCount(rangeStart, mid, index * 2 + 1, treeStart, mid) + getCount(mid + 1, rangeEnd, index * 2 + 2, mid + 1, treeEnd);
        }
    }

    private void add(int rank, int index, int start, int end) {
        if (start == end) {
            tree[index]++;
            return;
        }
        int mid = start + (end - start) / 2;
        if (rank <= mid) {
            add(rank, index * 2 + 1, start, mid);
        } else {
            add(rank, index * 2 + 2, mid + 1, end);
        }
        tree[index] = tree[index * 2 + 1] + tree[index * 2 + 2];
    }
}

最后

看在博主这么努力，熬夜肝的情况下，给个免费的三连吧！