2016国赛
题目描述
X 星球的机器人表演拉拉队有两种服装,A 和 B。
他们这次表演的是搭机器人塔。
类似:
A
B B
A B A
A A B B
B B B A B
A B A B B A
队内的组塔规则是:
A 只能站在 AA 或 BB 的肩上。
B 只能站在 AB 或 BA 的肩上。
你的任务是帮助拉拉队计算一下,在给定 A 与 B 的人数时,可以组成多少种花样的塔。
输入描述
输入一行两个整数 M,N(0<M,N≤50),分别表示 A、B 的人数,保证人数合理性。
输出描述
要求输出一个整数,表示可以产生的花样种数。
输入输出样例
输入
1 2输出
3
题目大意
给出A,B两类机器人,让它们按—定规则堆成三角形塔,问可堆成的方案数
规则:
A只能放在AA,BB上B只能放在AB,BA上
思考:如何确定每一个方案
- 问题转换成:确定第一层(最下一层)的A,B分布情况即可
因为第一行确定了,第二次也随之确定(根据组塔规则),以此类推,所有的机器人的位置都是确定的。
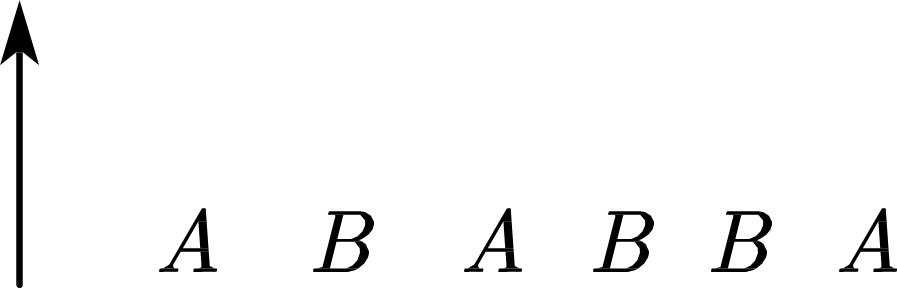
机器人的层数由机器人数量决定,,n最大可取到13,所以最多13层。一个位置可以放A和B两种,所以第一层最多能放
种,这个计算量不高。
A,B两个状态的表示
二进制法:
用0表示A,用1表示B
从最后一层向上递推的过程:
递推的结果符合异或运算的性质
解题思路:二进制枚举+异或运算递推
1、根据输入的A,B机器人数推算层数n:
2、二进制法求底层AB的所有情况
3、对于每个底层,利用异或运算(^)不断向上递推,递推过程中根据二进制数0,1统计A,B机器人剩余未使用的个数
4、如果A,B剩余未使用的个数出现负数,或者到达最顶层时A、B机器人个数不全为0,那么这个方案无效
5、统计所有有效的方案数,即为结果
代码:
d = {} # 存机器人数和层数
base = 0
for i in range(1, 20):
base += i # 机器人数
d[base] = i
M, N = map(int, input().split())
level = d[M + N] # 根据机器人数算出有多少层
def dfs(cur, clv, m, n): # cur:当前情况,clv:当前层数(最底层的机器人个数),m:剩余A的人数,n:剩余B的人数
if m < 0 or n < 0: # 排除出现负数的情况
return False
if clv == 0: # 层数为0
return m == n == 0
cb = bin(cur)[2:].count('1') # 转为二进制:0bxxxx(字符串),统计1的个数count('1')
ca = clv - cb # 不直接统计0的个数,因为例如001010最前面的两个0没办法计入
m -= ca; n -= cb
up = (cur ^ (cur >> 1)) & ((1 << (clv - 1)) - 1) # 计算出上一层的情况
return dfs(up, clv - 1, m, n) # 搜索上一层(层数-1)
res = 0
for case in range(1 << level): # 遍历2^n种情况
if dfs(case, level, M, N):
res += 1
print(res)注:下面对代码up = (cur ^ (cur >> 1)) & ((1 << (clv - 1)) - 1) 进行解释
例如:cur为22(二进制位10110),clv为6
1、cur >> 1:将cur右移一位,右移一位为1011;
1 << (clv - 1):1向左移动clv-1位,为01111
2、 (cur ^ (cur >> 1)):求上一层的情况,但最左边多出来一位
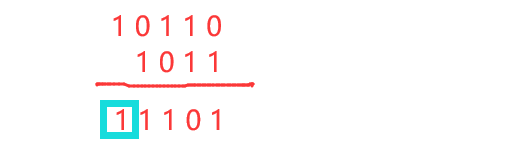
3、& ((1 << (clv - 1)) - 1):和一个二进制位为01111相与(&)就能去掉最左边的一位。注意“-”的优先级大于“>>”,所以需要加一个括号让<<先算。