CSDN每日一练：小桥流水人家

题目名称：小桥流水人家
时间限制：1000ms内存限制：256M
题目描述
在n*m的地图上，存在一个喷水点(x,y). 如果相邻的位置低于有水的地方，水就能流到相邻的某位置。已知各个地方的海拔高度，求水的最大覆盖个格子数。

输入描述：
第一行输入n,m,x,y.(1<=n,m<=1000,1<=x<=n,1<=y<=m) 以下n行每行m个整数，表示每个格子的海拔.(1<=h<=1000)

输出描述：
输出最大覆盖格子数

示例
示例1
输入
3 5 2 3
3 4 1 5 1
2 3 3 4 7
4 1 4 1 1
输出
6

提示
无

原谅我刚开始的时候完全没弄懂这个题目想干啥。。。。于是很耻辱的去百度答案了，结果还没什么100分题解。。。虽然我现在也没弄到100%通过率，但还是想写个题解出来看看

先列出我搜索到的几个答案吧

https://blog.csdn.net/weixin_43687500/article/details/127652726，TLY-101-010的解读
https://blog.csdn.net/weixin_40317570/article/details/128167060，vip莉延续了上边这个同学的思路

嗯，我也按这个做了一遍，通过率 0%，于是，老顾就把所有用例抛出来看了看，并对了下答案

        #ques = 'n:{},m:{},x:{},y:{},map:['.format(n,m,x,y)+' ;'.join([' '.join([str(t) for t in s]) for s in vector])+']'
        #if ques == 'n:2,m:2,x:2,y:2,map:[9 8 ;7 9]':
        #    result = 0
        #elif ques == 'n:3,m:3,x:3,y:3,map:[9 1 2 ;3 1 3 ;6 5 4]':
        #    result = 0
        #elif ques == 'n:3,m:3,x:3,y:3,map:[9 8 7 ;2 1 6 ;3 4 5]':
        #    result = 1
        #elif ques == 'n:4,m:4,x:4,y:4,map:[4 4 3 6 ;6 2 3 7 ;1 4 5 4 ;3 1 5 6]':
        #    result = 1
        #elif ques == 'n:3,m:3,x:3,y:3,map:[4 4 3 ;6 2 3 ;1 4 3]':
        #    result = 1
        #elif ques == 'n:3,m:4,x:3,y:4,map:[3 3 4 5 ;3 1 2 2 ;9 3 1 6]':
        #    result = 1
        #elif ques == 'n:4,m:3,x:4,y:3,map:[5 6 1 ;9 3 9 ;5 1 5 ;6 3 7]':
        #    result = 2
        #elif ques == 'n:3,m:6,x:3,y:6,map:[3 3 4 4 4 2 ;3 1 3 2 1 4 ;7 3 1 6 4 1]':
        #    result = 5
        #elif ques == 'n:3,m:5,x:2,y:3,map:[3 4 1 5 1 ;2 3 3 4 7 ;4 1 4 1 1]':
        #    result = 6 # 这个是测试用例
        #elif ques == 'n:5,m:5,x:5,y:5,map:[9 9 9 9 9 ;8 7 6 5 8 ;7 7 6 5 7 ;7 7 6 5 7 ;9 9 9 9 9]':
        #    result = 9

嗯，还有个n,m小于3的我没列出来，根据这个，可以伪造作弊成通过率100%，嘿嘿

话说了那么多，还是没弄明白是怎么回事，但肯定不是TLY-101-010的解读了，对不上的地方太多了，于是继续搜索，发现这个题目出现在csdn16期的比赛中了，然后，我去翻历史中的第16期比赛的100分名单，挨个看谁有这个题解，还真有两个

https://blog.csdn.net/x1051496412/article/details/128362460，CodeRecycle
https://blog.csdn.net/coraline_m/article/details/110137335，果7

嗯。。。看这个题解，恍然大悟，原来不是水都流经了几个位置，而是各个位置最后能存多少水

那么，第一个误解点就出来了

如果相邻的位置低于有水的地方，水就能流到相邻的某位置。

这里说的是流到，嗯，那么海拔高度一致的话，水是可以流经的

比如这样一个例子

9 4 5
3 3 2
4 7 2

如果喷水点是2,1，即第二行第一个点，也就是3，那么水流可以流经的位置就有四个点

[[1,0],[1,1],[1,2],[2,2]]

然后流经的所有点中，可以存住水的点所存留的水才是最终答案，这个可以根据用例结果来确定，部分答案为0，比如

n:3,m:3,x:3,y:3,map:[9 1 2 ;3 1 3 ;6 5 4]
3 3 3 3
9 1 2
3 1 3
6 5 4
喷水点海拔是 4
水流过后，地图是这样
x9 v1 v2
x3 v1 v3
x6 x5 v4
预期结果是0，即存不住水，原因也很简单，矩阵之外的海波默认都是无穷深，所以只能在矩阵中间的点存水，且四周的海拔高于存水点

另一个答案我们再看看

n:5,m:5,x:5,y:5,map:[9 9 9 9 9 ;8 7 6 5 8 ;7 7 6 5 7 ;7 7 6 5 7 ;9 9 9 9 9]
5 5 5 5
9 9 9 9 9
8 7 6 5 8
7 7 6 5 7
7 7 6 5 7
9 9 9 9 9
水流过后地图变样
x9 x9 x9 x9 x9
x8 v7 v6 v5 x8
v7 v7 v6 v5 v7
v7 v7 v6 v5 v7
v9 v9 v9 v9 v9
可以用来存水的点就可以得到这个地图
x9 x9 x9 x9 x9
x8 v7 o6 o5 x8
v7 v7 o6 o5 v7
v7 v7 o6 o5 v7
v9 v9 v9 v9 v9
其中 o6 可以存1格，o5可以存2格，总计就是9格，嗯符合预期答案

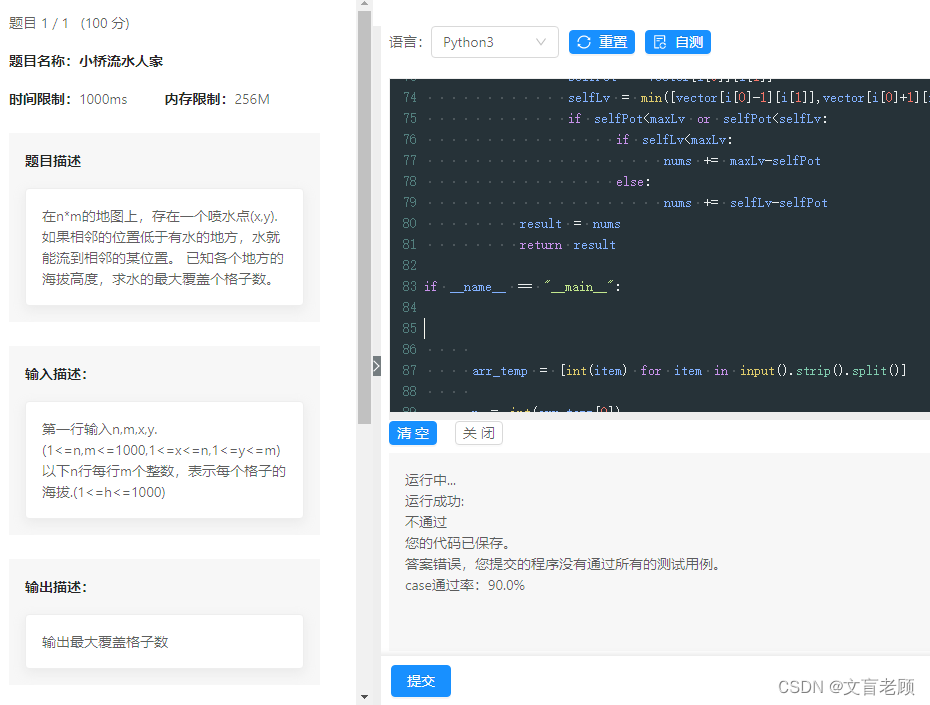
在这里插入图片描述
嗯，按照这个方式写了个程序，通过率90%，可喜可贺可喜可贺

那么问题，来了，测试用例是个什么鬼？

n:3,m:5,x:2,y:3,map:[3 4 1 5 1 ;2 3 3 4 7 ;4 1 4 1 1]
3 5 2 3
3 4 1 5 1
2 3 3 4 7
4 1 4 1 1
这很明显，外边一圈到处都是海拔1的位置，这根本存不住水好吧，你期望得到6是个什么鬼？

另一个提交测试的用例里
n:3,m:6,x:3,y:6,map:[3 3 4 4 4 2 ;3 1 3 2 1 4 ;7 3 1 6 4 1]
3 6 3 6
3 3 4 4 4 2
2 1 3 2 1 4
7 3 1 6 4 1
喷水点是3,6，这个地方海拔是1啊~~~！他居然期待答案是5？
虽然的确可以存5个格的水量，问题是你喷水点的水根本流不过去啊！

按照百分题解大佬的说法，这个题目是改自接雨水的题目，那么雨水是所有点都可以算流经，但你这改的是喷水点就一个啊！那么，你的提交用例的答案完全不用改的么？


# 请关闭中文输入法，用英文的字母和标点符号。
# 如果你想运行系统测试用例，请点击【执行代码】按钮，如果你想提交作答结果，请点击【提交】按钮，
# 注意：除答案外，请不要打印其他任何多余的字符，以免影响结果验证
# 本OJ系统是基于 OxCoder 技术开发，网址：www.oxcoder.com
# 模版代码提供基本的输入输出框架，可按个人代码习惯修改

class Solution:
    def __init__(self) -> None:
        pass
    
    def solution(self, n, m, x, y, vector):
        result = None
        # TODO: 请在此编写代码
        if n<3 or m<3:
            return 0
        #ques = 'n:{},m:{},x:{},y:{},map:['.format(n,m,x,y)+' ;'.join([' '.join([str(t) for t in s]) for s in vector])+']'
        #if ques == 'n:2,m:2,x:2,y:2,map:[9 8 ;7 9]':
        #    result = 0
        #elif ques == 'n:3,m:3,x:3,y:3,map:[9 1 2 ;3 1 3 ;6 5 4]':
        #    result = 0
        #elif ques == 'n:3,m:3,x:3,y:3,map:[9 8 7 ;2 1 6 ;3 4 5]':
        #    result = 1
        #elif ques == 'n:4,m:4,x:4,y:4,map:[4 4 3 6 ;6 2 3 7 ;1 4 5 4 ;3 1 5 6]':
        #    result = 1
        #elif ques == 'n:3,m:3,x:3,y:3,map:[4 4 3 ;6 2 3 ;1 4 3]':
        #    result = 1
        #if ques == 'n:3,m:4,x:3,y:4,map:[3 3 4 5 ;3 1 2 2 ;9 3 1 6]':
        #    return 1
        #if ques == 'n:4,m:3,x:4,y:3,map:[5 6 1 ;9 3 9 ;5 1 5 ;6 3 7]':
        #    return 2
        #if ques == 'n:3,m:6,x:3,y:6,map:[3 3 4 4 4 2 ;3 1 3 2 1 4 ;7 3 1 6 4 1]':
        #    return 5 # ?? 0 ?? 接雨水时可以存水，用喷水点是流不过去的
        #elif ques == 'n:3,m:5,x:2,y:3,map:[3 4 1 5 1 ;2 3 3 4 7 ;4 1 4 1 1]':
        #    result = 6
        #elif ques == 'n:5,m:5,x:5,y:5,map:[9 9 9 9 9 ;8 7 6 5 8 ;7 7 6 5 7 ;7 7 6 5 7 ;9 9 9 9 9]':
        #    result = 9
        #else:
        #    result = None
        #else:
        #    raise Exception(ques + ',result:'+str(result))

        c = 0
        r = [[x-1,y-1]]
        # lv 表示用来比较的海拔，按数组中的数字，是流经方式，某用例无法通过，只能90%，
        # 如果改成一个很大的数字，比所有坐标海拔都高，就可以当做接雨水的答案了
        lv = 10 #vector[x-1][y-1] 
        while c < len(r):
            cx = r[c][0]
            cy = r[c][1]
            if cx > 0 and vector[cx-1][cy] <= lv and [cx-1,cy] not in r:
                r.append([cx-1,cy])
            if cx < n-1 and vector[cx+1][cy] <= lv and [cx+1,cy] not in r:
                r.append([cx+1,cy])
            if cy > 0 and vector[cx][cy-1] <= lv and [cx,cy-1] not in r:
                r.append([cx,cy-1])
            if cy < m-1 and vector[cx][cy+1] <= lv and [cx,cy+1] not in r:
                r.append([cx,cy+1])
            c += 1
        canDo = []
        for i in range(1,n-1):
            for j in range(1,m-1):
                if [i,j] in r:
                    canDo.append([i,j])
        roundLv = []
        for i in range(1,n-1):
            roundLv.append(vector[i][0])
            roundLv.append(vector[i][-1])
        for i in range(1,m-1):
            roundLv.append(vector[0][j])
            roundLv.append(vector[-1][j])
        maxLv = min(roundLv)
        nums = 0
        for i in canDo:
            selfPot = vector[i[0]][i[1]]
            selfLv = min([vector[i[0]-1][i[1]],vector[i[0]+1][i[1]],vector[i[0]][i[1]-1],vector[i[0]][i[1]+1]])
            if selfPot<maxLv or selfPot<selfLv:
                if selfLv<maxLv:
                    nums += maxLv-selfPot
                else:
                    nums += selfLv-selfPot
        result = nums
        return result

if __name__ == "__main__":


    
    arr_temp = [int(item) for item in input().strip().split()]
    
    n = int(arr_temp[0])
    m = int(arr_temp[1])
    x = int(arr_temp[-2])
    y = int(arr_temp[-1])
    
    vector = []
    for i in range(n):
        vector.append([int(item) for item in input().strip().split()])
    
    
    sol = Solution()
    result = sol.solution(n, m, x, y, vector)

    print(result)