LeetCode 84. 柱状图中最大的矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。求在该柱状图中,能够勾勒出来的 矩形的最大面积。
视频讲解文章讲解![]() https://programmercarl.com/0084.%E6%9F%B1%E7%8A%B6%E5%9B%BE%E4%B8%AD%E6%9C%80%E5%A4%A7%E7%9A%84%E7%9F%A9%E5%BD%A2.html#%E5%8F%8C%E6%8C%87%E9%92%88%E8%A7%A3%E6%B3%95
https://programmercarl.com/0084.%E6%9F%B1%E7%8A%B6%E5%9B%BE%E4%B8%AD%E6%9C%80%E5%A4%A7%E7%9A%84%E7%9F%A9%E5%BD%A2.html#%E5%8F%8C%E6%8C%87%E9%92%88%E8%A7%A3%E6%B3%95
- 思路:
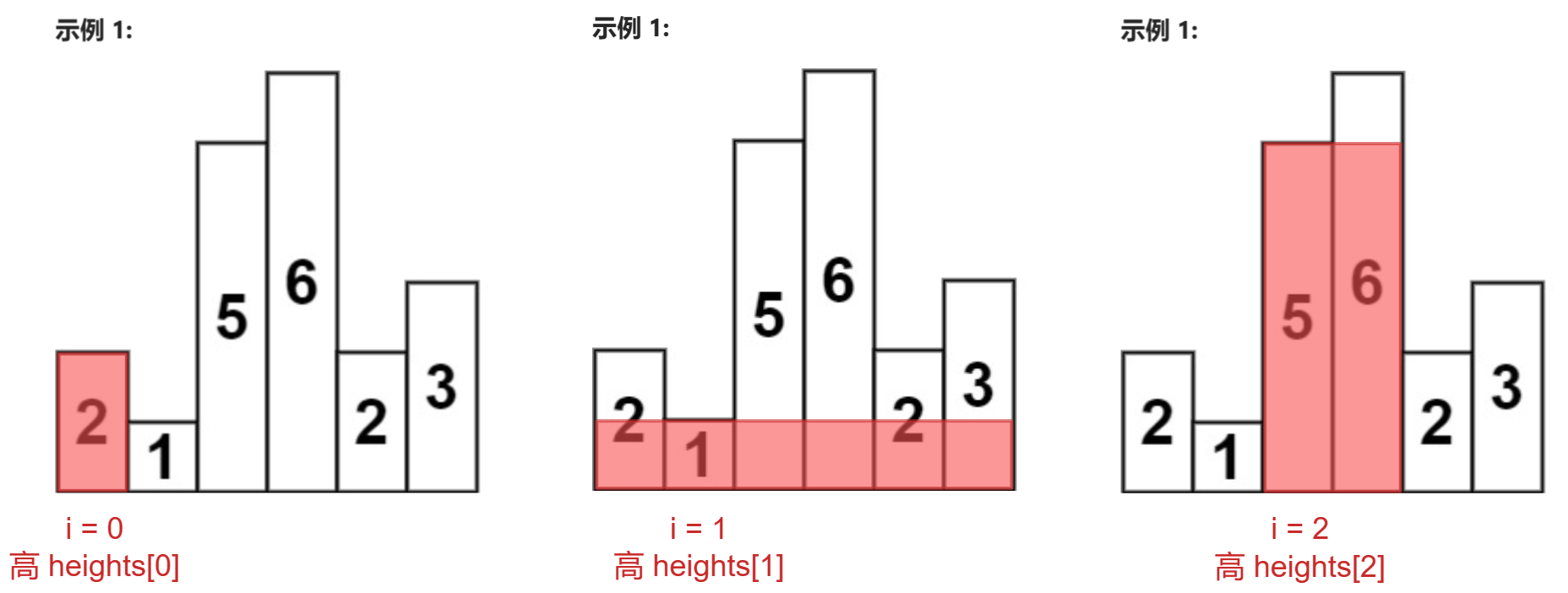
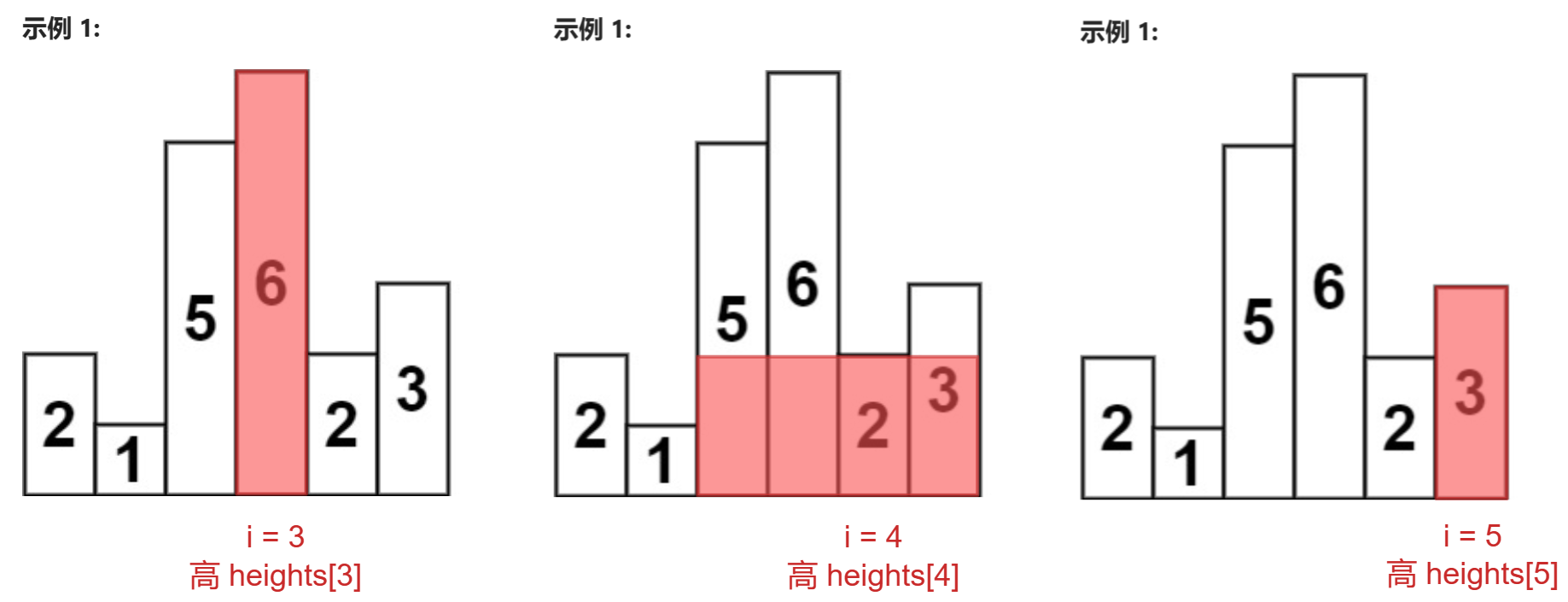
- 双指针解法:对于每一个i,以heights[i]为矩形的长,找最大宽度,求得面积来更新 result
- 从 i 出发,向左找第一个高度小于 heights[i] 的柱子,记其下标为 left
- 从 i 出发,向右找第一个高度小于 heights[i] 的柱子,记其下标为 right
- 最大宽度(left, right)👉right - left - 1
- result = max(result, (right - left - 1) * heights[i]);
- 动态规划解法:两个dp数组
- 数组 minLeftIndex:记录每个柱子 左边第一个低于该柱子的下标
- 数组 minRightIndex:记录每个柱子 右边第一个低于该柱子的下标
- 注意:minLeftIndex vs 接雨水 maxLeft
- 左(右)边第一个低于 i 的柱子 vs 左边最高的柱子
- 下标 vs 高度
- 循环查找 vs 直接由 maxLeft[i - 1] 与 i 高度取大
- 单调栈解法:
- 从栈顶到栈底(高度)递减;
- height[st.top()] == height[i],有两种处理思路:
- 出栈旧下标,入栈新下标:相当于保留等高柱的最右一个
- 直接令 i 入栈,栈中柱子高度不是严格单调递减:相当于以等高柱的最左一个计算实际的最大宽度,并更新result
- 自己:
- height[st.top()] > height[i]:right = i
- 以栈顶柱子高度为矩形的长:int h = height[st.top()];
- 以栈顶第二个元素下标为 left,矩形的最大宽度(left, i)👉i - left - 1
- 如果没有栈顶第二个元素,left 为 -1
- 单独处理栈中剩余元素,height[st.top()] > 0,right = heights.size()
- height[st.top()] > height[i]:right = i
- 代码随想录:数组首尾分别加入元素0
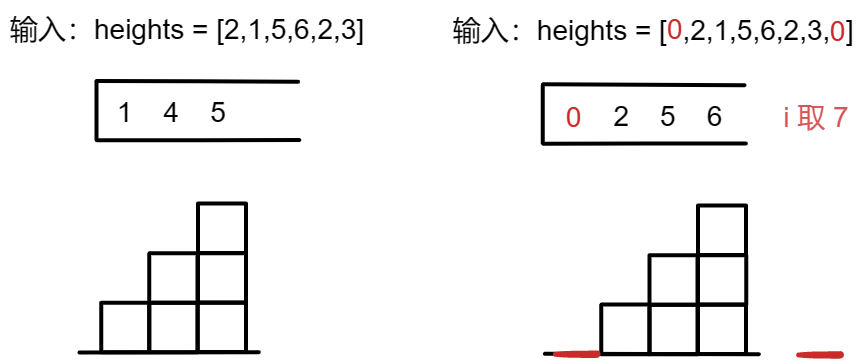
左:直接处理原数组 右:数组首尾分别加入元素 0
for循环结束后 for循环结束后
需单独处理栈中剩余元素 所有元素都已经处理完
- 双指针解法:对于每一个i,以heights[i]为矩形的长,找最大宽度,求得面积来更新 result
- 代码:
// 双指针:
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int sum = 0;
for (int i = 0; i < heights.size(); i++) {
int left = i;
int right = i;
for (; left >= 0; left--) {
if (heights[left] < heights[i]) break;
}
for (; right < heights.size(); right++) {
if (heights[right] < heights[i]) break;
}
int w = right - left - 1;
int h = heights[i];
sum = max(sum, w * h);
}
return sum;
}
};
// 时间复杂度:O(n^2)
// 空间复杂度:O(1)// 动态规划:
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
vector<int> minLeftIndex(heights.size());
vector<int> minRightIndex(heights.size());
int size = heights.size();
// 记录每个柱子 左边第一个小于该柱子的下标
minLeftIndex[0] = -1; // 注意这里初始化,防止下面while死循环
for (int i = 1; i < size; i++) {
int t = i - 1;
// 这里不是用if,而是不断向左寻找的过程
while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
minLeftIndex[i] = t;
}
// 记录每个柱子 右边第一个小于该柱子的下标
minRightIndex[size - 1] = size; // 注意这里初始化,防止下面while死循环
for (int i = size - 2; i >= 0; i--) {
int t = i + 1;
// 这里不是用if,而是不断向右寻找的过程
while (t < size && heights[t] >= heights[i]) t = minRightIndex[t];
minRightIndex[i] = t;
}
// 求和
int result = 0;
for (int i = 0; i < size; i++) {
int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
result = max(sum, result);
}
return result;
}
};// 单调栈:
// 版本一:从栈顶到栈底严格单调递减
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> st;
heights.insert(heights.begin(), 0); // 数组头部加入元素0
heights.push_back(0); // 数组尾部加入元素0
st.push(0);
int result = 0;
// 第一个元素已经入栈,从下标1开始
for (int i = 1; i < heights.size(); i++) {
// 注意heights[i] 是和heights[st.top()] 比较 ,st.top()是下标
if (heights[i] > heights[st.top()]) {
st.push(i);
} else if (heights[i] == heights[st.top()]) {
st.pop(); // 这个可以加,可以不加,效果一样,思路不同
st.push(i);
} else {
while (heights[i] < heights[st.top()]) { // 注意是while
int mid = st.top();
st.pop();
int left = st.top();
int right = i;
int w = right - left - 1;
int h = heights[mid];
result = max(result, w * h);
}
st.push(i);
}
}
return result;
}
};
// 精简版:合并情况一、二,从栈顶到栈底非严格单调递减(栈中可以有高度相同的柱子)
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> st;
heights.insert(heights.begin(), 0); // 数组头部加入元素0
heights.push_back(0); // 数组尾部加入元素0
st.push(0);
int result = 0;
for (int i = 1; i < heights.size(); i++) {
while (heights[i] < heights[st.top()]) {
int mid = st.top();
st.pop();
int w = i - st.top() - 1;
int h = heights[mid];
result = max(result, w * h);
}
st.push(i);
}
return result;
}
};