1、双指针

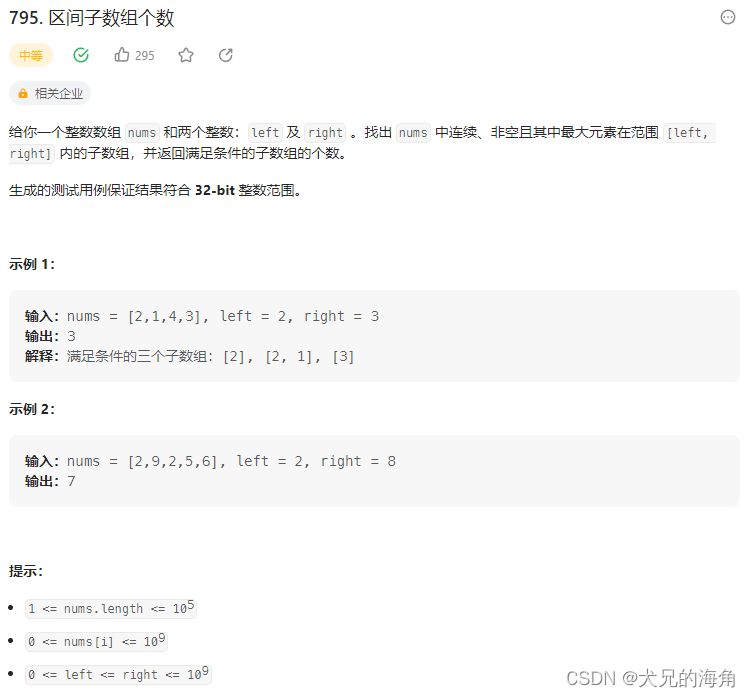
根据题意，我们可以将数组中的数分为这三类：1、小于$left$的数；2、大于等于$left$且小于等于$right$的数；3、大于$right$的数。因此若我们使用双指针来维护区间$[last2,last1]$，其中我们让$last1$指向大于等于$left$且小于等于$right$的数，$last2$指向大于$right$的数。因此当我们遍历每个位置$i$时，此时区间右顶点固定在$i$，左区间顶点可以落在$(last2,last1]$中，我们只要统计左区间顶点可能的个数即可。

class Solution {
public:
    int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {
        int res = 0, last2 = -1, last1 = -1;
        for (int i = 0; i < nums.size(); i++) {
            if (nums[i] >= left && nums[i] <= right) {
                last1 = i;
            } else if (nums[i] > right) {
                last2 = i;
                last1 = -1;
            }
            if (last1 != -1) {
                res += last1 - last2;
            }
        }
        return res;
    }
};

2、双指针优化

由于我们在方法一中所求的区间个数实质上是不包含第三类且至少包含一个第二类的数的区间，因此我们可以求出只包含第一类和第二类数字的区间总数，而后减去只包含第一类区间数字的总数即可。

class Solution {
public:
    int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {
        return count(nums, right) - count(nums, left - 1);
    }

    int count(vector<int>& nums, int lower) {
        int res = 0, cur = 0;
        for (int x : nums) {
            cur = x <= lower ? cur + 1 : 0;
            res += cur;
        }
        return res;
    }
};