目录
- 问题引出
- 库选择与绘制准备
- plot3d类api简介
- 图像绘制与参数说明
- 关键字参数
- 绘图举例
- 绘图的案例
- 三角函数
- 另一个三角函数
问题引出
在求解二元函数最值的时候,我们不知道自己经过若干个步骤求出的结果是否正确,那么我们该怎么办呢?一种办法就是将这个函数的图像绘制出来
三维图像的作用在于,它不仅能让我们直观的看出待求二元函数在指定区间内的形状,而且对于我们求得的最值以及求极值的步骤有着重要的指导意义
库选择与绘制准备
matplotlib是一个比较基础的专业绘图库,它也可以用来绘制三维图像,但是需要额外导入mpl_toolkits库,在前段时间学习sympy库时注意到了它里面的plotting子模块,里面封装了若干个绘图类,其中的一个plot3d类可以实现三维绘图,而且调用十分方便
注意,sympy中的绘图类仍然使用matplotlib库提供的后端支持,也就是说使用sympy绘图类需要首先安装
matplotlib库
plot3d类api简介
plot3d(*args, show=True, **kwargs)
图像绘制与参数说明
同一坐标系内绘制单个图像
plot3d(expr, range_x, range_y, **kwargs)
| 参数 | 描述 |
|---|---|
| expr | 函数表达式 |
| range_x,range_y | 变量x,y的取值区间(默认区间为[-10,10]) |
在同一坐标系内绘制双图像(两个二元函数)
plot3d(expr1,expr2, range_x, range_y, **kwargs)
同一坐标系内绘制多个图像(多个二元函数)
plot3d((expr1, range_x, range_y),(expr2, range_x, range_y,) ,...,**kwargs)
关键字参数
| 参数名 | 数据类型 | 描述 |
|---|---|---|
| nb_of_points_x | int | 在该参数处对x取值范围均匀采样 |
| nb_of_points_y | int | 在该参数处对y取值范围均匀采样 |
| surface_color | Function which returns a float | 绘出图像的颜色 |
| title | str | 图像标题 |
| size | (float, float) | 图像尺寸 |
绘图举例
下面例子来自sympy官网
# 单图像
from sympy import symbols
from sympy.plotting import plot3d
x, y = symbols('x y')
plot3d(x*y, (x, -5, 5), (y, -5, 5))
运行结果
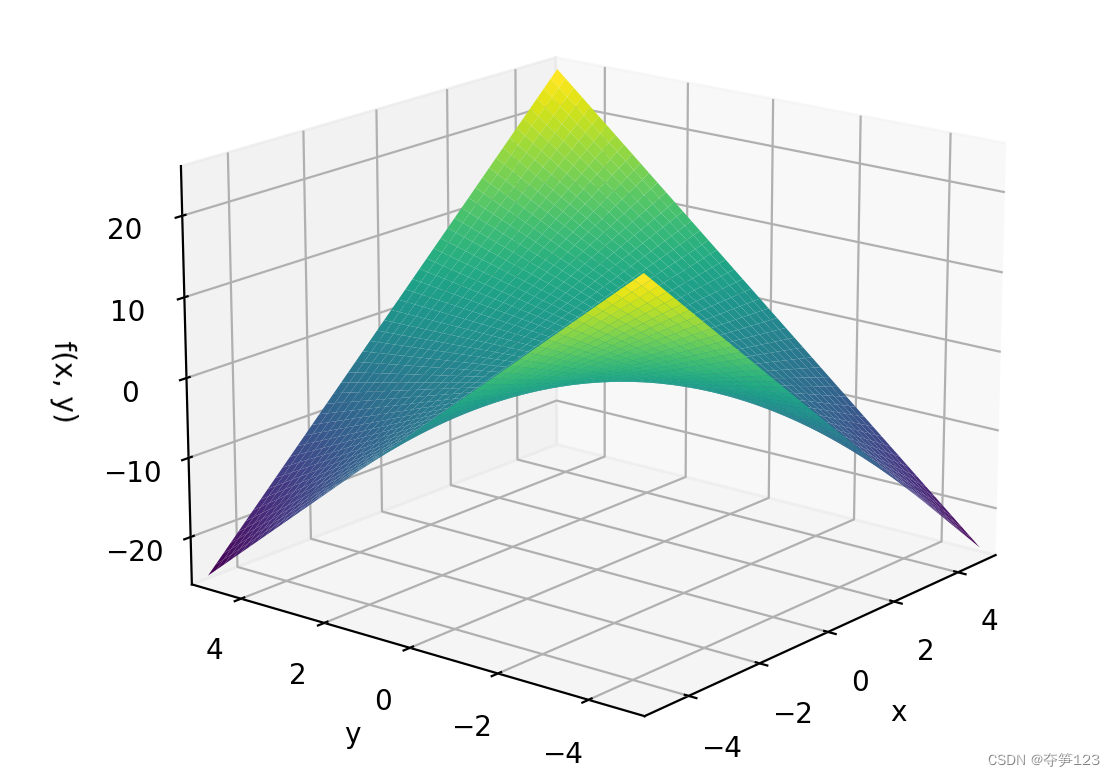
# 双图像
plot3d(x*y, -x*y, (x, -5, 5), (y, -5, 5))
运行结果
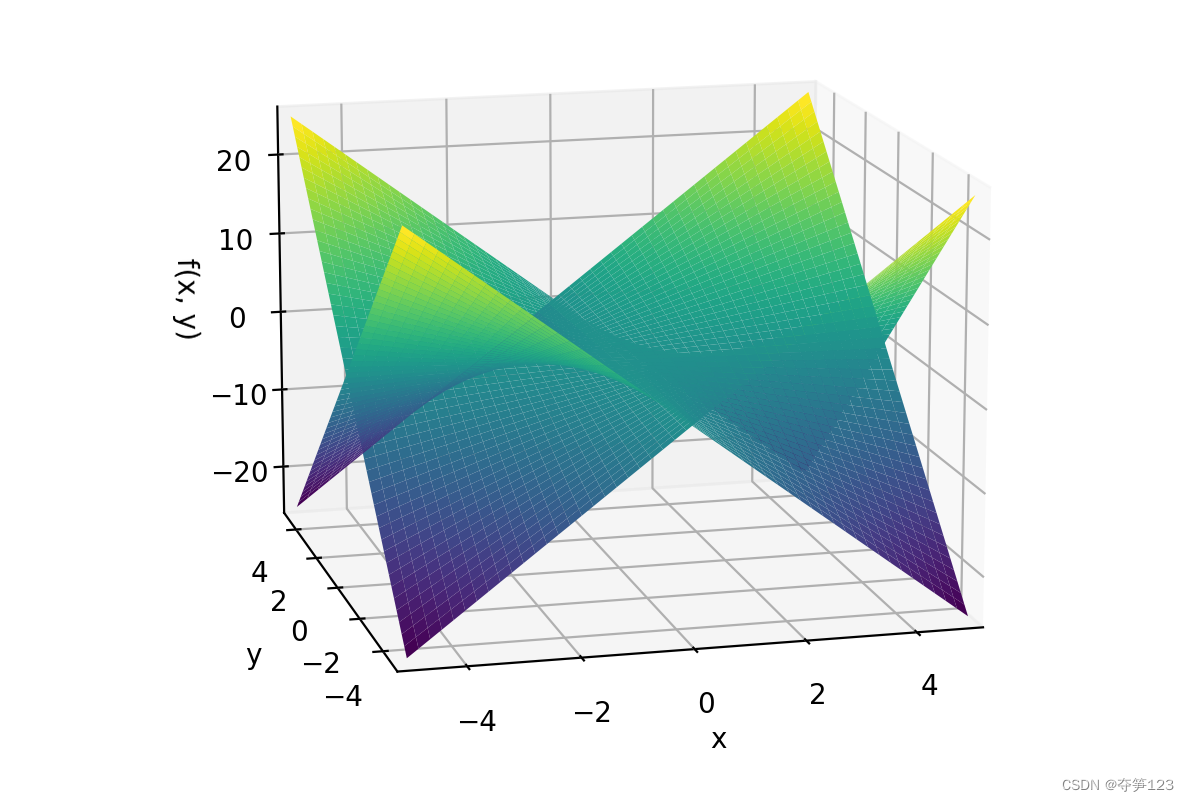
# 多图像
plot3d((x**2 + y**2, (x, -5, 5), (y, -5, 5)),
(x*y, (x, -3, 3), (y, -3, 3)))
运行结果
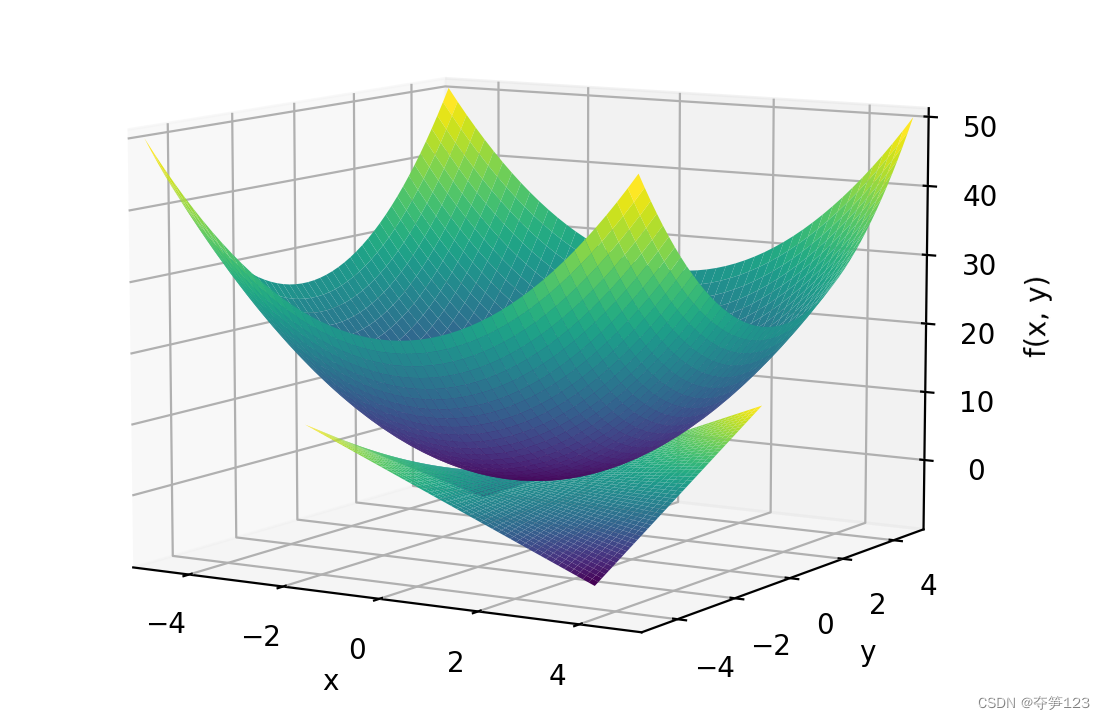
绘图的案例
读完了plot3d的api,我们尝试解决一些实际问题
三角函数
绘制 y = s i n x 2 + y 2 , x ∈ [ − 5 , 5 ] , y ∈ [ − 5 , 5 ] 的图像,并找出其最小值对应的坐标 绘制y=sin\sqrt{x^2+y^2},x\in [-5,5],y\in [-5,5]的图像,并找出其最小值对应的坐标 绘制y=sinx2+y2,x∈[−5,5],y∈[−5,5]的图像,并找出其最小值对应的坐标
代码实现
from sympy import symbols
from sympy.plotting import plot3d
from sympy import *
x, y = symbols('x y')
plot3d(sin(sqrt(x**2+y**2)),(x, -5, 5), (y, -5, 5))
运行结果

注意看图像窗口的右上角,它代表三维图像上的点,会随着鼠标的指向而发生变化,虽然sympy绘图类不会返回给我们精确地函数最值,但是我们可以通过观察图像、拖动图像来找到函数最值得大概位置,这就是绘制出图像的意义所在
另一个三角函数
实际上,这篇博客的灵感来源于笔者最近在学习的模拟退火算法,该算法的其中一个应用方向是求带约束的二元函数极值,由于参数设置等的不同,导致对于同一个二元函数运行同样的程序,每次得到的函数极值各不相同,但是笔者也不知道哪次得到的极值是正确的,然后看到了这篇博客
用模拟退火算法求解带约束的二元函数极值问题之二:用MATLAB绘图验证
实际上很多时候,可视化能够解决很多想象不到的问题,于是笔者也想要尝试一下使用python进行可视化,这个例子中仍然使用原博客中的二元函数
f ( x , y ) = 6 x 2 + x 2 + y 2 + 5 s i n ( x ) + 3 c o s ( y ) + 50 x ∈ [ − 5 , 5 ] , y ∈ [ − 5 , 5 ] f(x,y)=\frac{6x}{2+x^2+y^2}+5sin(x)+3cos(y)+50\\x\in[-5,5],y\in[-5,5] f(x,y)=2+x2+y26x+5sin(x)+3cos(y)+50x∈[−5,5],y∈[−5,5]
代码实现
from sympy import symbols
from sympy.plotting import plot3d
from sympy import *
x, y = symbols('x y')
expr=6*x/(2+x**2+y**2)+5*sin(x)+3*cos(y)+50
plot3d(expr,(x, -5, 5), (y, -5, 5))
运行结果
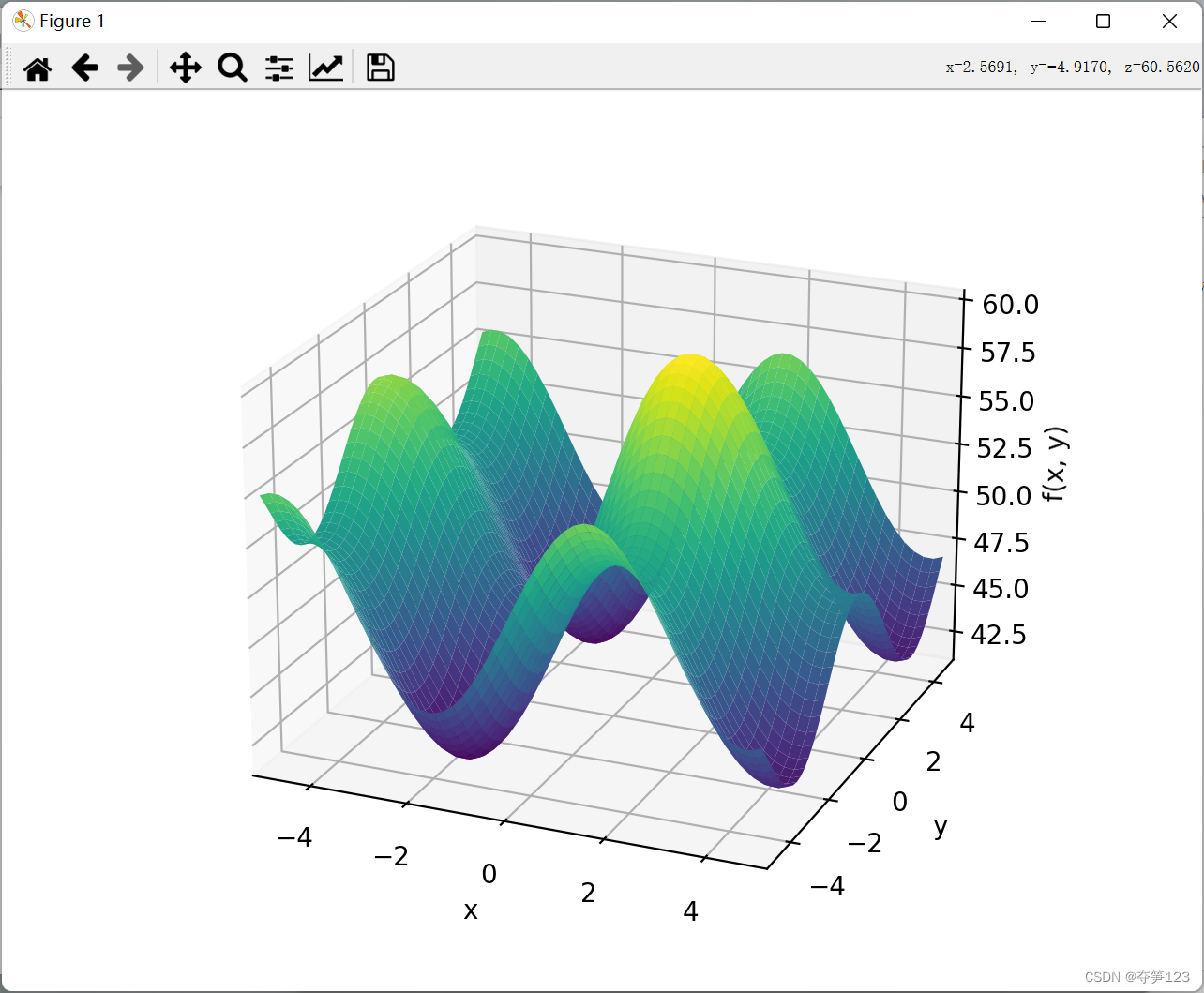
从上面的图中我们可以看出该二元函数的函数值范围大约在[42.5,60]之间,这就为我们的算法求解提供了一个方向