在LTI系统的时域分析中，输入信号被分解成冲激信号或阶跃信号的叠加（积分），然后利用LIT 的 线性和时不变性可以推出系统的零状态响应等于输入信号与系统冲激响应的卷积。我们将仍然沿用信号分解这一思想对信号和系统进行分析，不过， 我们将对信号在正弦信号或虚指数信号组成的信号集合（空间）上做正交分解，然后引出系统频率响应的概念，介绍系统的频域分析方法。
能分解其实就是利用的是数学上的傅里叶分解，通过用简单的信号的线性组合来完成对复杂信号的分解处理。只需要对单个单个信号处理，再合并在一起就可以得到我们想要的结果。就像下面的方波，可以用很多频率的三角波合成。分解量也称阶数越大，拟合效果越好。

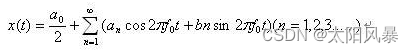
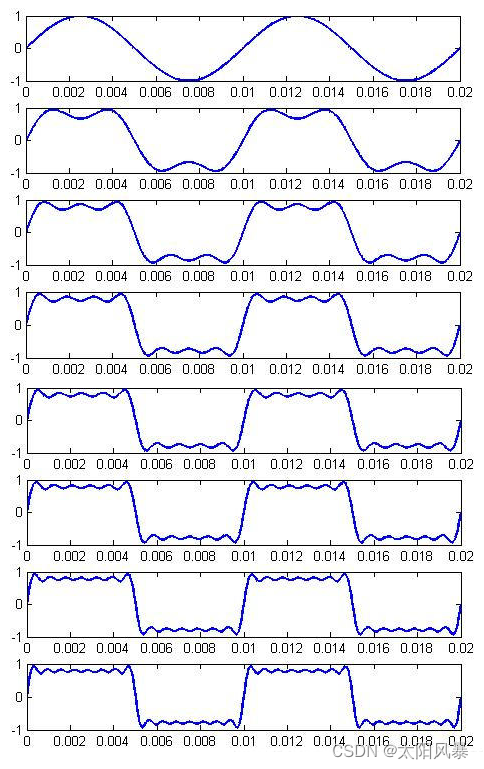
（这里借鉴一下图 原链接）

一、正交函数集

为便于进行信号分析，常常将复杂的信号分解为一些基本信号的线性组合，例如在连续时间系统的时域分析中，以冲激函数或阶跃函数作为基本信号，系统的零状态响应表示为输入信号与系统冲激响应的卷积。

二、三角形式傅里叶级数

将任意一个周期信号在三角函数或复指数函数组成的完备正交函数集分解得到
的级数，统称为傅立叶级数（Fourier Series，FS）。他们具有如下一些显著优点：

• ① 三角函数和复指数函数是自然界中最常见，最基本的函数；
• ② 三角函数和复指数函数是简谐函数，用它们表示时间信号，自然地建立起了时间和频率这两个基本物理量间的联系；
• ③ 简谐信号较其他信号更容易产生和处理；
• ④ 三角信号或复指数信号通过线性时不变系统后，仍为三角函数和复指数函数，其频率不变，只是幅度和相位产生变化，同时，线性时不变系统对三角函数或复指数函数的响应求解非常方便；
• ⑤ 许多系统（例如滤波器、信息传输系统等）的特性主要由其频域特性来描述，因此常常需要关心的并不是这些系统的冲激响应，而是其冲激响应所对应的频率特性；
• ⑥ 时域中的卷积运算在频域中会转化为乘积运算，从而找到了计算卷积的一种新方法，使时域中难于实现的卷积求解便于实现

如果一个函数是周期的，满足

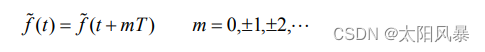
则信号可以展开成如下级数的形式

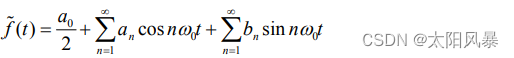
其中 ω₀ 称为信号的基波角频率：

对函数的级数展开式进行积分
可以得到 a₀ 的值

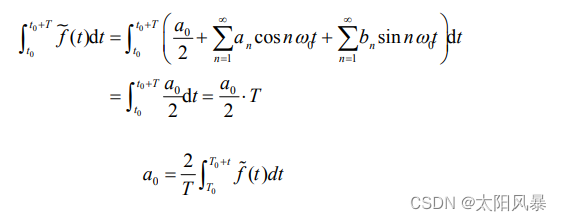
直接看公式


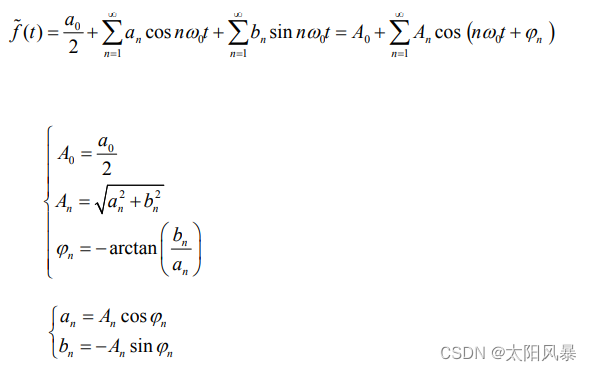
例题：

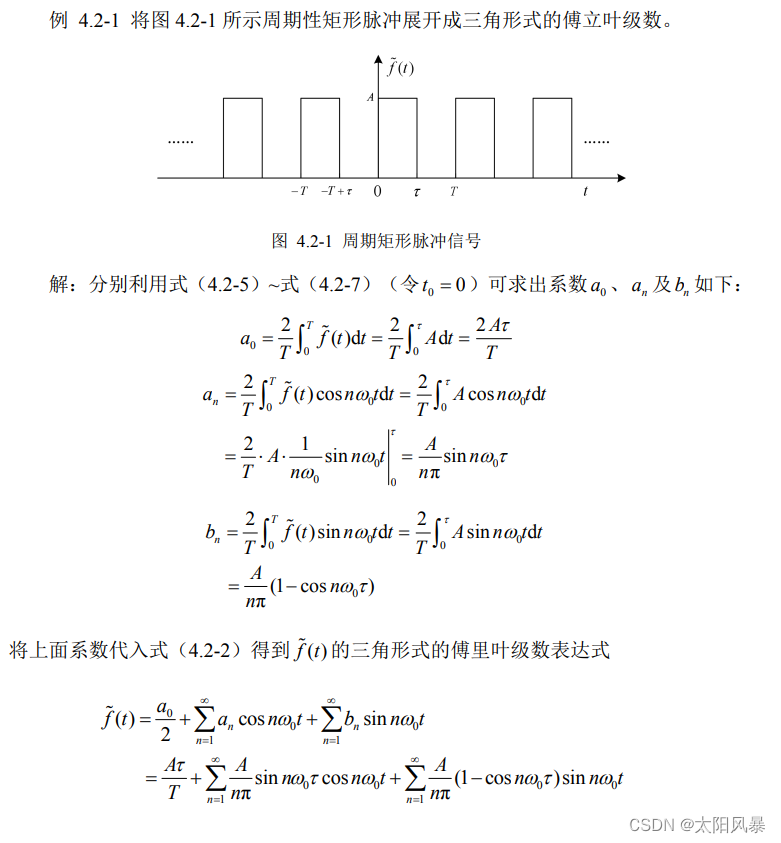
三、指数形式的傅里叶级数

1. 定义

周期信号可以分解成如下形式。

其中ω₀ 仍为信号的基波角频率。上式的表示形式称为指数形式的傅里叶级数，在没有特别说明的情况下，傅里叶级数一般指的是指数形式的傅里叶级数。

2. 系数确定

将 定义式 两边乘以 e^-jmω0t

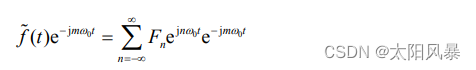
将上式在一个周期内（令 t₀ = 0）同时对两边积分，得：

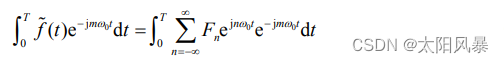
交换上式右端积分与求和次序得：

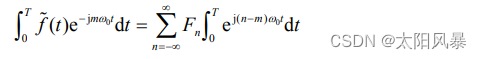
其中上式右端的积分利用欧拉公式展开得:

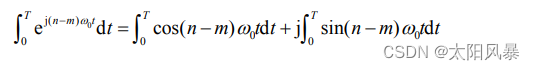
上面积分在n ≠ m 时等于 0，在n = m 时等于T ，即：

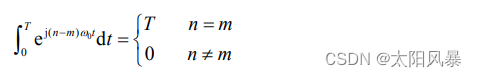
只有当n = m 时不等于 0，此时有：

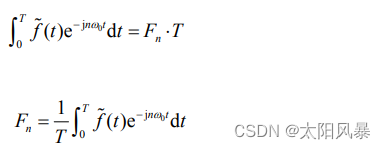
综上所述，周期信号的傅里叶级数对可以完整地表示成：

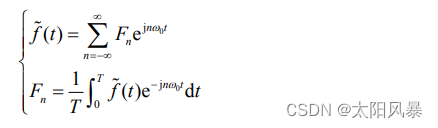
F_n通常称为 f(t) 的复指数形式傅里叶级数系数或频谱系数。这些复数系数是对f(t)中每一个谐波分量的大小作出的度量。

一个信号可以用三角形式和指数形式同时表示，可以通过欧拉公式转换

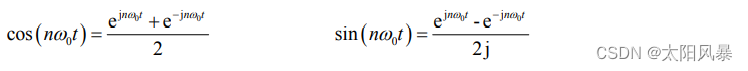
转换代入如下

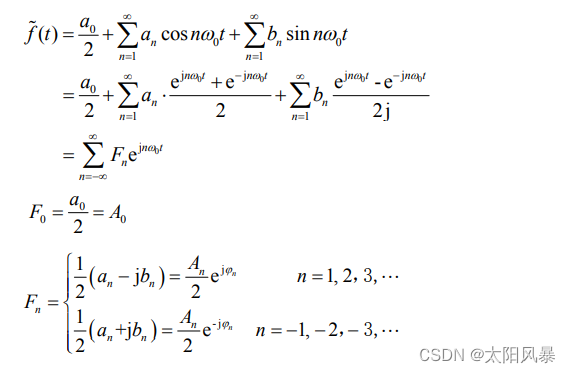
再转换一下

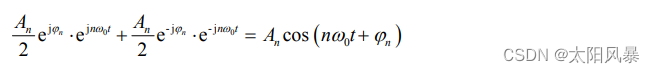
3. 典型信号的傅里叶级数

例题1：

这个其实就是用了 下面这个公式

例题2：

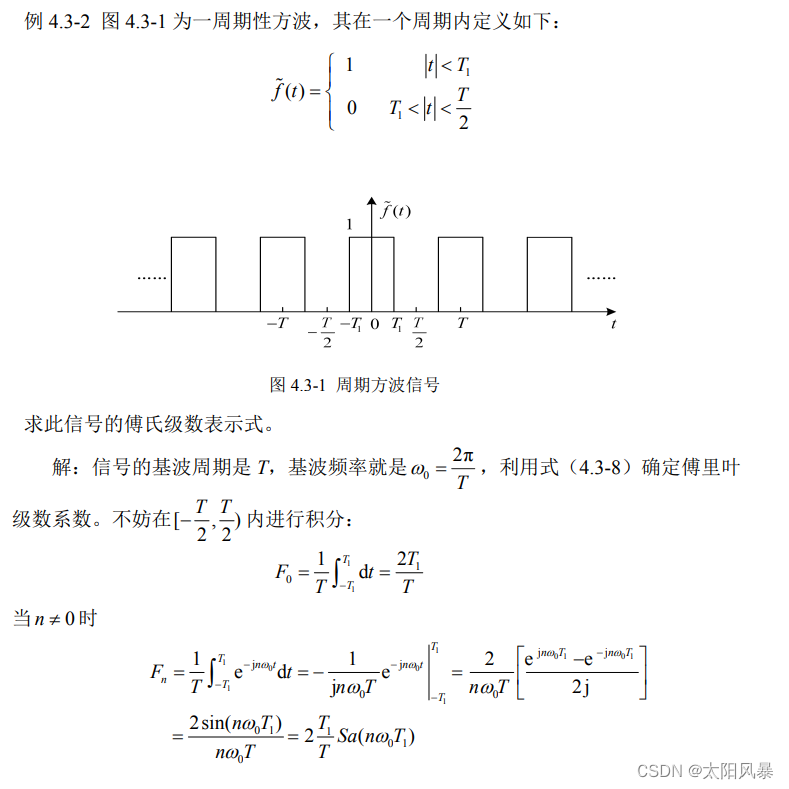
例题3：

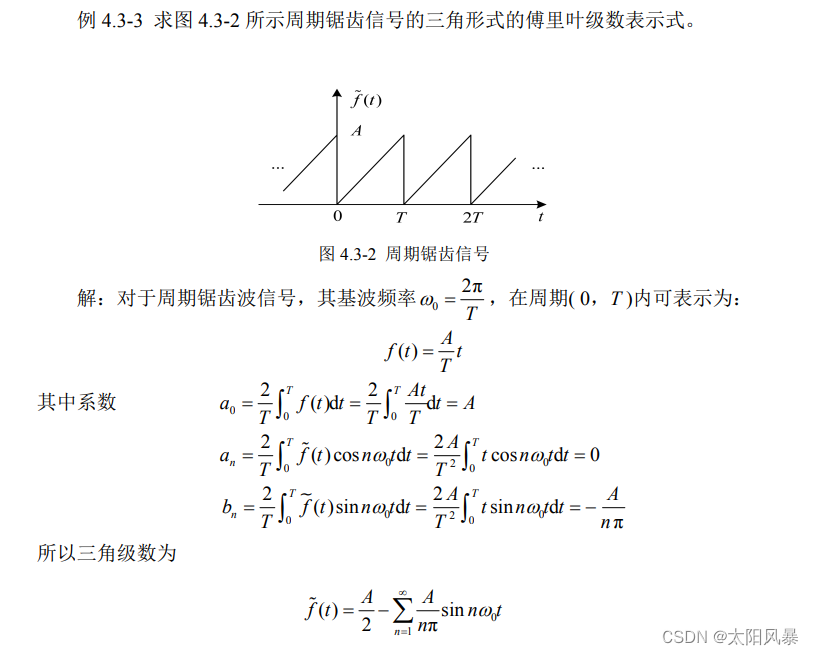
例题4：

一个周期信号与另一个周期信号的区别，在时域上表示为不同波形，而在频域中表现为 A_n(F_n) 不同，即振幅和相位的
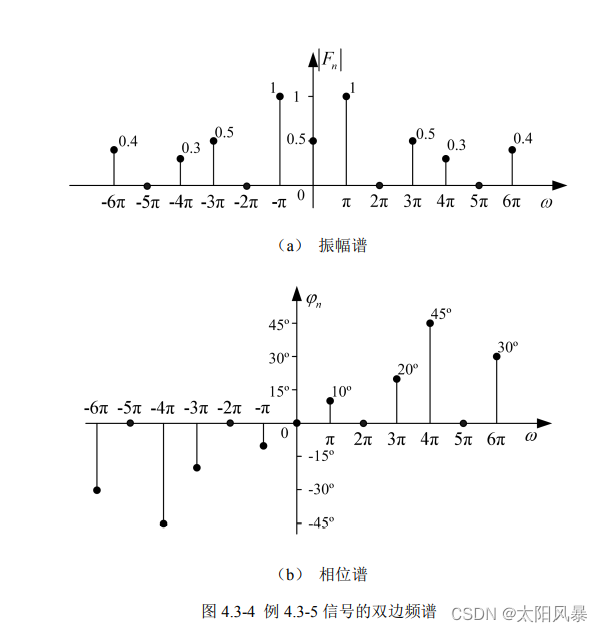
不同。而复振幅 A_n(F_n) 为在频域研究信号 ω₀ 的关键，为了既方便又明确地表示一个信号中包含有哪些频率分量，各分量所占的比重如何，特画出振幅 A_n(F_n) 及相位 ψ_n 随 ω 变化的曲线，从而得到一种谱线图，称为频谱图。该图一般包括两幅图形，即振幅频谱和相位频谱。

• 振幅频谱，也称幅度谱，是以 ω 为横坐标，以振幅 A_n(F_n) 为纵坐标所画出的谱线图；
• 相位频谱（也称相位谱）则是以 ω 为横坐标，以相位 ψ_n 为纵坐标所得到的图形。

在信号的复振幅 A_n(F_n) 为 nω₀ 的实函数的特殊情况下， A_n(F_n) 与 nω₀ 的关系也可以用一个图形给出。

例题：

• 三角形式
  
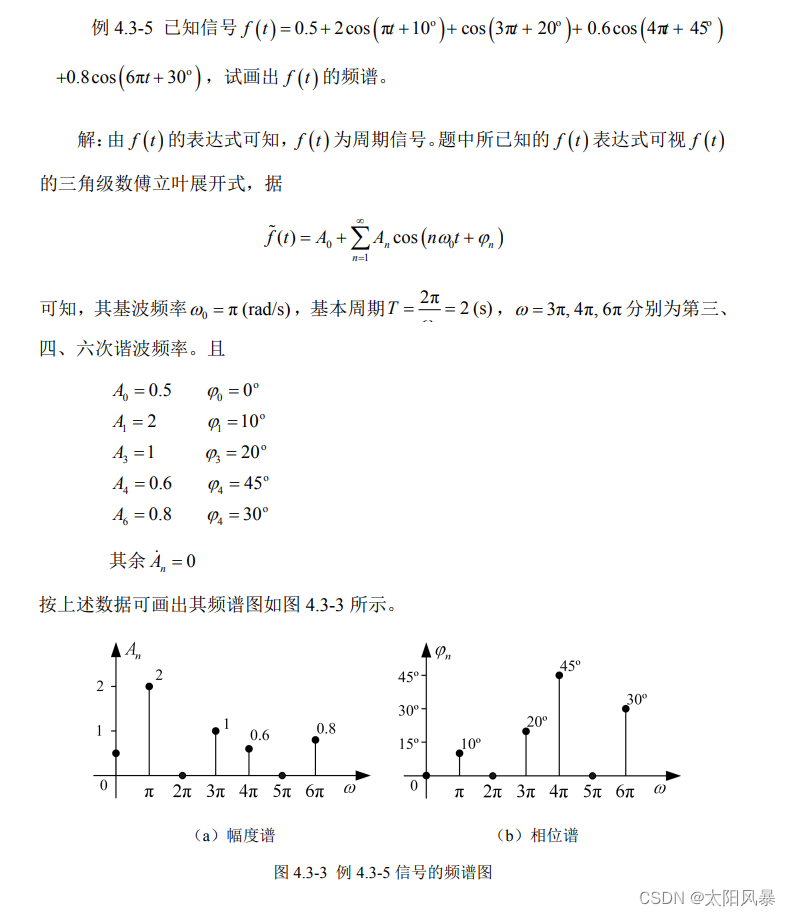
• 指数形式
  用的是下面公式来换
  
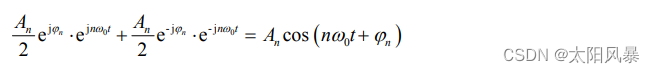
  幅度减半，相位相反，由两个指数形式叠加的
  

4. 周期信号的功率谱

周期信号属于功率信号，其平均功率定义为1 Ω 电阻上所消耗的平均功率