2022 APMCM亚太数学建模竞赛 C题 全球是否变暖 思路及代码实现(持续更新中)
1 题目
全球变暖与否? 加拿大49.6°C的高温为地球北纬50°以上地区创造了新的气温记录,一周内就有数百人死于高温;美国加利福尼亚州死亡谷54.4°C,是地球上有记录以来的最高温度;科威特53.5°C,阳光直射下甚至超过70°C,中东很多国家超过50°C。
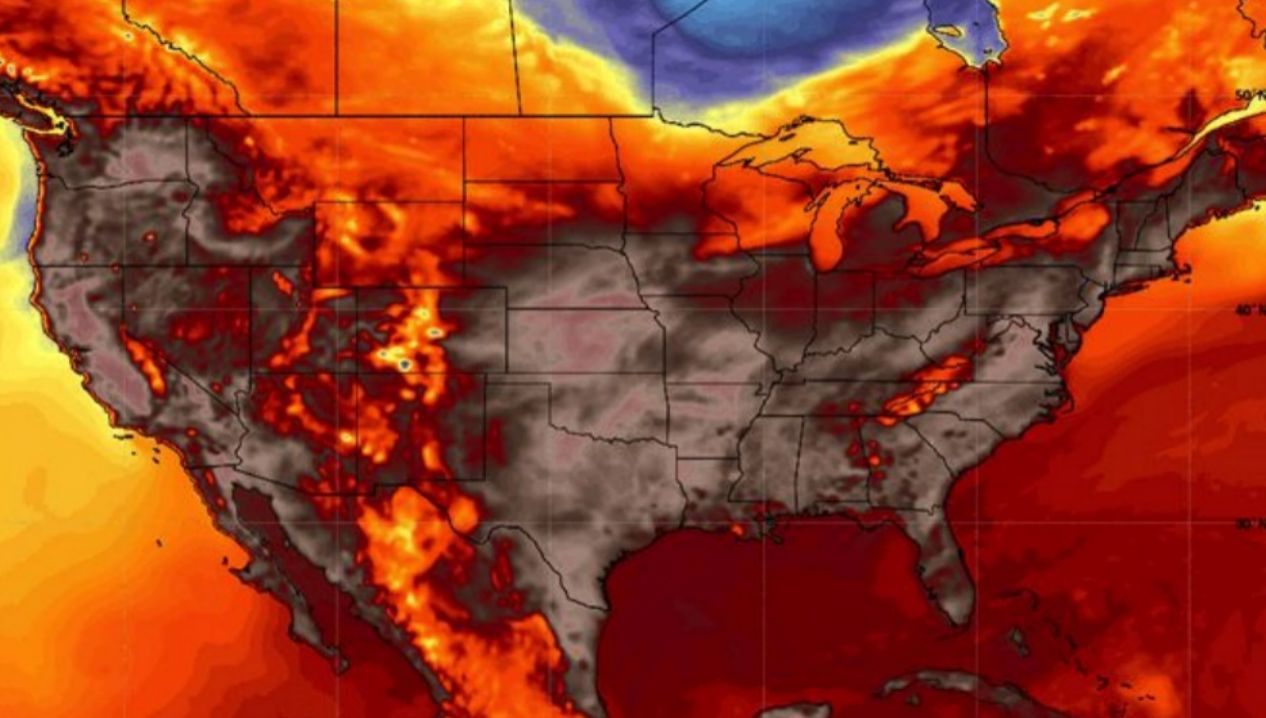
图1所示。北美的高温。 今年以来,我们看到了大量惊人的气温报告。地球正在燃烧的事实是毋庸置疑的。继这些地区从6月底到7月初的可怕高温之后,意大利再次创下欧洲气温纪录,达到惊人的48.8°C,许多国家宣布进入紧急状态。
全球气候变暖是一种与自然有关的现象。正是由于温室效应的不断积累,导致地球大气系统吸收和排放的能量失衡,能量在地球大气系统中不断积累,导致气温上升,全球气候变暖。
在工业革命之前,二氧化碳(CO2大气中的二氧化碳一直保持在280 ppm左右。2004年3月,大气中的二氧化碳浓度达到了377.7 ppm,这是到那时为止10年平均增幅最大的一次。根据美国国家海洋和大气管理局(NOAA)和斯克里普斯海洋学研究所(SIO)的科学家们的研究,月平均CO2 浓度水平在2022年5月达到峰值421 ppm。经济合作与发展组织(OECD)的一份报告预测CO2 到2050年,二氧化碳浓度将达到685 PPM
APMCM组委会已要求您的团队解决这些关于当前报告和未来全球温度水平预测的主张。他们提供了数据集2022_APMCM_C_Data.csv,其中包含239177条记录,以协助你们的研究。
需求 1.你同意全球温度的说法吗?使用附件中的2022_APMCM_C_Data.csv和你们团队收集的其他数据集来分析全球温度变化。
a)你是否同意2022年3月全球温度的上升导致了比以往任何10年期间观测到的更大的增长?为什么?为什么不? b)基于历史数据,请建立两个或两个以上的数学模型来描述过去并预测未来的全球温度水平。 c)分别使用1(b)中的每个模型来预测2050年和2100年的全球温度。你们的任何一个模型是否与2050年或2100年观测点的全球平均温度将达到20.00°C的预测一致?如果不是在2050年或2100年,你们预测模型中观测点的平均温度什么时候会达到20.00°C?
d)你在1(b)中建立的哪个模型你认为最准确?为什么? 2.影响温度变化的原因是什么? a)利用问题1的结果和附件2022_ APMCM_C_ data .csv和你们团队收集的其他数据集中的数据,建立一个数学模型来分析全球温度、时间和位置之间的关系(如果有),并解释它们之间的关系或证明它们之间没有关系。
b)请收集相关数据,分析自然灾害(如火山爆发、森林火灾和新冠肺炎)的因素。对全球气温有影响吗?
2 题目分析
2.1 问题一
(a)你是否同意2022年3月全球温度的上升导致了比以往任何10年期间观测到的更大的增长?为什么?为什么不?
思路:第一步,挑选几个城市,选取2022年的一整年的数据,将温度变化以折线图可视化,分析3月是不是存在异常值。
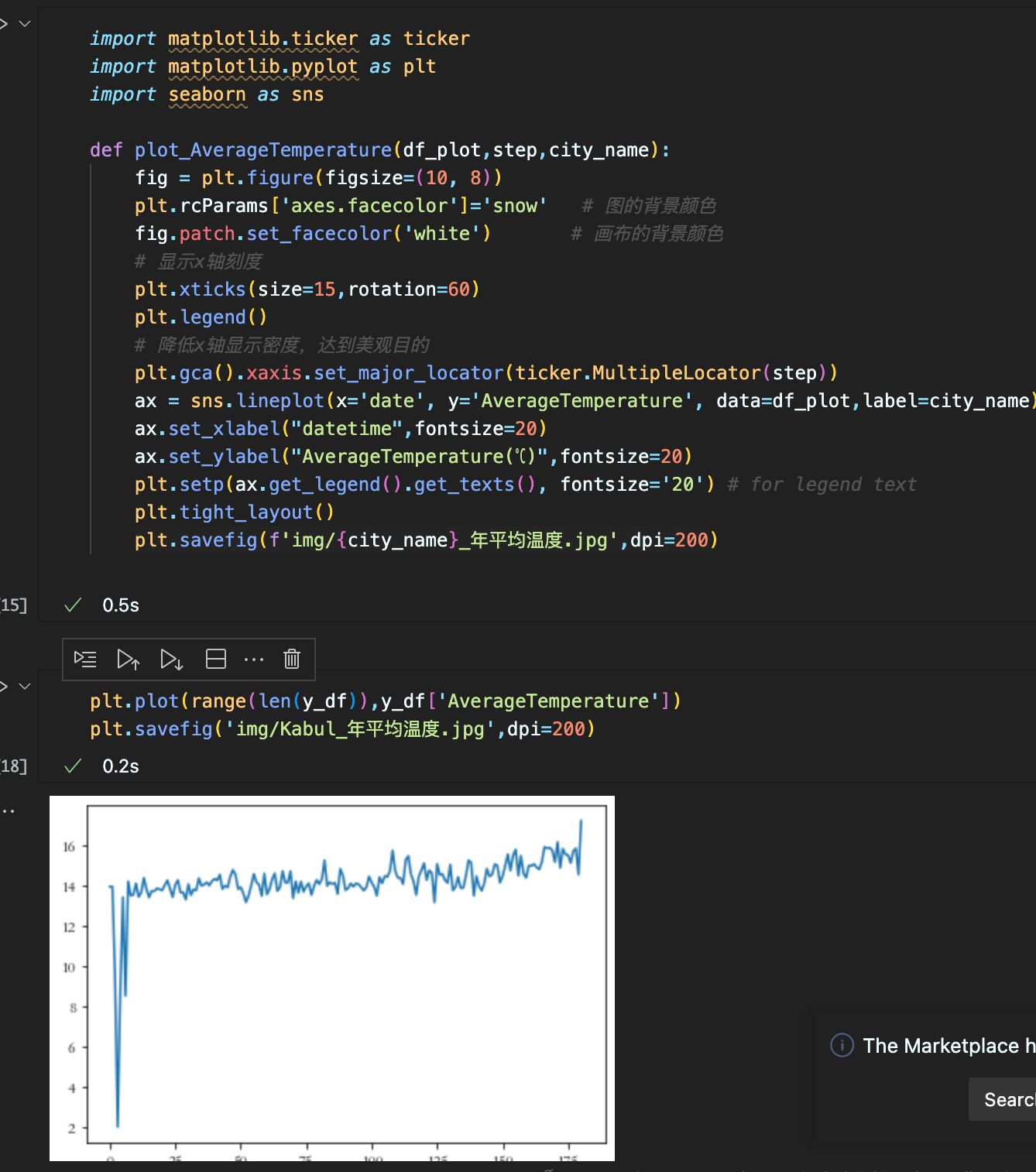
第二步,计算2022年排除3月的平均温度,和加上3月后的平均温度,计算2011年-2021年的平均温度,以折线图可视化。对比每年的增长,与2022年有无3月份数据的增长。
(b)基于历史数据,请建立两个或两个以上的数学模型来描述过去并预测未来的全球温度水平。
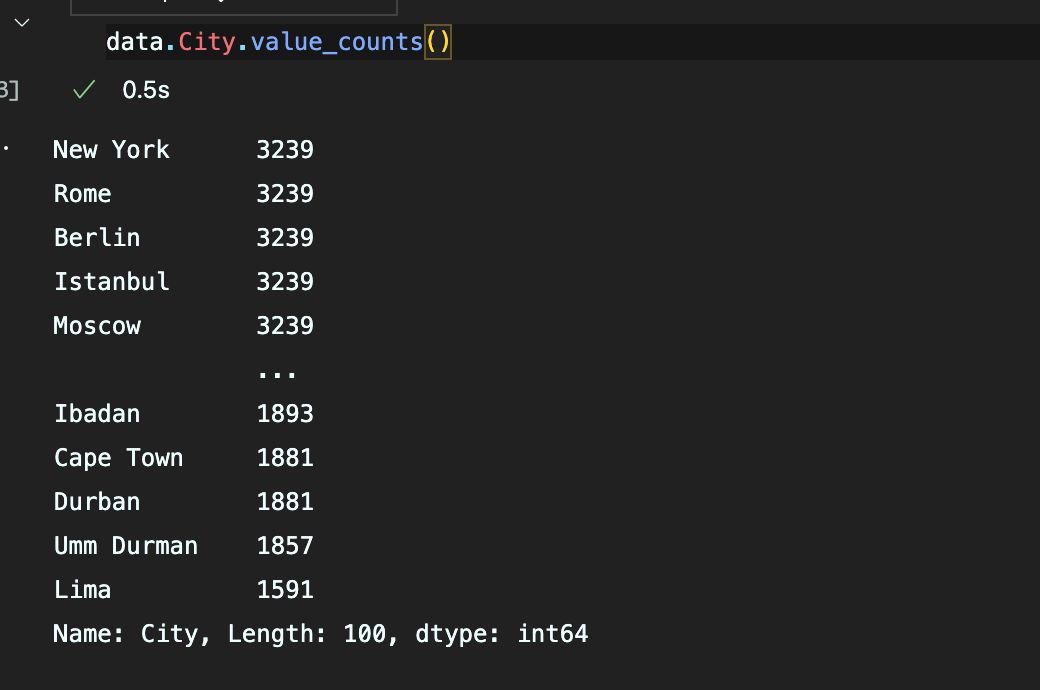
从(c)知道,需要以年为跨度,建立时间序列预测模型。通过分析虽然有100个城市,但在题目中,没指定说明哪个观测点。
随机挑一个城市即可。以年为时间单位,统计每年的平均温度,得到一个时间序列。选择以下时间序列预测模型进行预测即可。注意题目需要两个模型。
有哪些时间序列预测模型
- 自回归 (AR)
- 移动平均线
- 自回归移动平均线
- 自回归积分移动平均线 (ARIMA)
- 季节性自回归积分移动平均线 (SARIMA)
- 具有外生回归量的季节性自回归综合移动平均线 (SARIMAX)
- 具有 ARIMA 误差的回归模型
- 向量自回归 (VAR)
- GARCH 模型
- Glostan、Jagannathan 和 Runkle GARCH 模型
(c)利用以上模型,预测未来100年的平均温度,并将这100个数据,可视化,分析什么时候能达到20度。
(d)模型的准确性,用评价指标来评价
模型的评价指标有
(1)MSE(mean squared error),是观测值(observed values)与预测值(predicted values)的误差的平方和的均值,即SSE/n。它是误差的二阶矩,包含估计量的方差(variance)及其偏差(bias),是衡量估计量质量的指标,其公式为:
M S E ( y , y ^ ) = 1 n ∑ ( y i − y i ^ ) 2 MSE(y,\hat{y})=1n∑(yi−\hat{yi})2 MSE(y,y^)=1n∑(yi−yi^)2
(2)RMSE(root mean squared error),也称作RMSD(root mean square deviation),是MSE的算数平方根。由于每个误差(each error)对RMSD的影响与误差的平方(squared error)成正比,因此较大的误差会对RMSE影响过大,RMSE对异常值很敏感。其公式为:
R M S E ( y , y ^ ) = 1 n ∑ ( y i − y i ^ ) 2 RMSE(y,\hat{y})=1n∑(yi−\hat{yi})2 RMSE(y,y^)=1n∑(yi−yi^)2
(3)MAE(mean absolute error),是时间序列分析中预测误差常用的指标,由于MAE使用的是与被测数据相同的尺度(scale),因此不能用于比较两个不同尺度的序列。MAE又被称为L1范数损失函数(就是可以做为损失函数),是真实数据与预测数据之差的绝对值的均值。
M A E ( y , y ^ ) = 1 n ∑ ∣ y i − y i ^ ∣ MAE(y,\hat{y})=1n∑|yi−\hat{yi}| MAE(y,y^)=1n∑∣yi−yi^∣
(4)MAPE(mean absolute percentage error),也被称为MAPD(mean absolute percentage deviation),是一种衡量预测方法的预测准确性的指标。MAPE在解释相对误差(relative error)方面非常直观,在评价模型时MAPE通常用作回归(regression)问题的损失函数(loss function)。
M A P E ( y , y ^ ) = 1 n ∑ ∣ y i − y i ^ ∣ y MAPE(y,\hat{y})=1n∑|yi−\hat{yi}|y MAPE(y,y^)=1n∑∣yi−yi^∣y
2.2 问题二
(a)利用问题1的结果和附件2022_ APMCM_C_ data .csv和你们团队收集的其他数据集中的数据,建立一个数学模型来分析全球温度、时间和位置之间的关系(如果有),并解释它们之间的关系或证明它们之间没有关系。
分析经纬度与温度之间的相关性。做出热力图分析,分析是什么相关性
做出折线图分析平均气温随着经度或纬度的变化。用SPSS拟合模型,一般是多元线性回归模型。
(b)请收集相关数据,分析自然灾害(如火山爆发、森林火灾和新冠肺炎)的因素。对全球气温有影响吗?
待更新。。。
3 代码及文档下载
持续更新,最新更新通知会在群里第一时间发布
下载链接
https://mbd.pub/o/bread/Y5yYmpZs
QQ群:105235809,进群密目:下载内容中
本人团队,有23个比赛经验,我们参与的有8个,辅导其他团队的有15个比赛。在比赛期间,将会持续提供详细的指导方案,包括建模方案和代码实现,可以参考我历史博客,查看我每个比赛做出的贡献
BetterBench-数学建模入门到精通博客