高阶数据结构：二叉搜索树

news2024/10/6 14:30:37

本篇主要是在初级数据结构中介绍的二叉树的提升，了解二叉搜索树的特性。

文章目录

  • 一、二叉搜索树的概念
  • 二、二叉搜索树操作
    • 1、二叉搜索树的查找
    • 2、二叉搜索树的插入
    • 3、二叉搜索树的删除
  • 三、二叉搜索树的实现
  • 四、二叉搜索树的应用
  • 五、关于二叉树进阶面试题

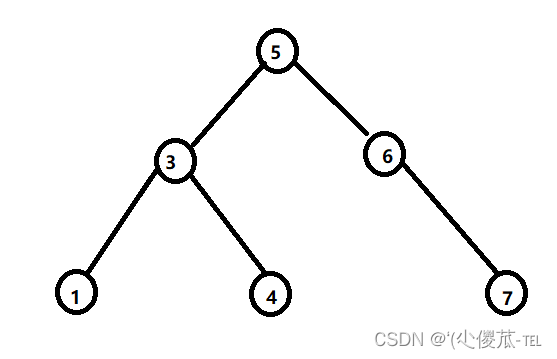
一、二叉搜索树概念

概念：二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下特征：

一、它的左子树不为空，则左子树上所有的节点的值都小于根节点的值

二、它的右子树不为空，则右子树上所有的节点的值都大于根节点的值

三、它的左右子树也分别为二叉搜索树

如果所示：

二、二叉搜索树的操作

1.二叉搜索树的查找

bool Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
				cur = cur->_right;
			else if(cur->_key>key)
				cur = cur->_left;
			else
			    return true;
		}
		return false;
	}

2.二叉树的插入

	bool Insert(const K& key)
	{
		//如果此时根结点不存在需要创建根结点
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}

		//插入新结点的时候需要将父类的节点进行连接
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		
		cur = new Node(key);
		if (parent->key < key)
			parent->_right = cur;
		else
			parent->_left = cur;
		return true;
	}

 3.二叉树的删除

bool Erase(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				//开始删除
				//左为空
				//右为空
				//左右都不为空
				//这里需要考虑根节点的情况
				if (cur->left == nullptr)
				{
					if (cur->_left == nullptr)
					{
						if (cur == _root)
						{
							_root = cur->_right;
						}
						else
						{
							if (cur == parent->_left)
								parent->left = cur->_right;
							else
								parent->_right = cur->right;
						}
					}
					delete cur;
					cur = nullptr;
				}
				else if (cur->_right == nullptr)
				{
					if (_root == cur)
						_root = cur->_left;
					else
					{
						if (cur == parent->_left)
							parent->_left = cur->_left;
						else
							parent->_right = cur->_left;
					}
					delete cur;
					cur = nullptr;
				}
				else
				{
					//找到右子树最小节点进行替换
					Node* minParent = cur;
					Node* min = cur->_right;
					while (min->_left)
					{
						minParent = min;
						min = min->_left;
					}
					swap(cur->_key, min->_key);
					if (minParent->_left == min)
						minParent->_left = min->_right;
					else
						minParent->_right = min->_right;
					delete min;
				}
				return true;
			}
			return false;
		}
	}

 三、二叉搜索树的实现

struct BSTreeNode
{
	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;
	K _key;

	BSTreeNode(const K& key)
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
	{}
};

//class BinarySearchTree
template<class K>
class BSTree
{
	typedef BSTreeNode<K> Node;
public:
	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		cur = new Node(key);
		if (parent->_key < key)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}

		return true;
	}

	bool Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else
			{
				return true;
			}
		}

		return false;
	}

	bool Erase(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				// 开始删除
				// 1、左为空
				// 2、右为空
				// 3、左右都不为空
				if (cur->_left == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}

					delete cur;
					cur = nullptr;
				}
				else if (cur->_right == nullptr)
				{
					if (_root == cur)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_left;
						}
					}

					delete cur;
					cur = nullptr;
				}
				else
				{
					// 找到右子树最小节点进行替换
					Node* minParent = cur;
					Node* min = cur->_right;
					while (min->_left)
					{
						minParent = min;
						min = min->_left;
					}

					swap(cur->_key, min->_key);
					if (minParent->_left == min)
						minParent->_left = min->_right;
					else
						minParent->_right = min->_right;

					delete min;
				}

				return true;
			}
		}

		return false;
	}

	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

	/
	bool FindR(const K& key)
	{
		return _FindR(_root, key);
	}

	bool InsertR(const K& key)
	{
		return _InsertR(_root, key);
	}

	bool EraseR(const K& key)
	{
		return _EraseR(_root, key);
	}

	~BSTree()
	{
		_Destory(_root);
	}

	/*BSTree()
	{}*/

	// C++的用法：强制编译器生成默认的构造
	BSTree() = default;

	BSTree(const BSTree<K>& t)
	{
		_root = _Copy(t._root);
	}

	// t2 = t1
	BSTree<K>& operator=(BSTree<K> t)
	{
		swap(_root, t._root);
		return *this;
	}

private:
	Node* _Copy(Node* root)
	{
		if (root == nullptr)
		{
			return nullptr;
		}

		Node* copyRoot = new Node(root->_key);
		copyRoot->_left = _Copy(root->_left);
		copyRoot->_right = _Copy(root->_right);
		return copyRoot;
	}

	void _Destory(Node*& root)
	{
		if (root == nullptr)
		{
			return;
		}

		_Destory(root->_left);
		_Destory(root->_right);
		delete root;
		root = nullptr;
	}


	bool _EraseR(Node*& root, const K& key)
	{
		if (root == nullptr)
			return false;

		if (root->_key < key)
			return _EraseR(root->_right, key);
		else if (root->_key > key)
			return _EraseR(root->_left, key);
		else
		{
			Node* del = root;
			if (root->_left == nullptr)
			{
				root = root->_right;
			}
			else if (root->_right == nullptr)
			{
				root = root->_left;
			}
			else
			{
				// 找右树的最左节点替换删除
				Node* min = root->_right;
				while (min->_left)
				{
					min = min->_left;
				}
				swap(root->_key, min->_key);
				//return EraseR(key);  错的
				return _EraseR(root->_right, key);
			}

			delete del;
			return true;
		}
	}

	bool _InsertR(Node*& root, const K& key)
	{
		if (root == nullptr)
		{
			root = new Node(key);
			return true;
		}

		if (root->_key < key)
			return _InsertR(root->_right, key);
		else if (root->_key > key)
			return _InsertR(root->_left, key);
		else
			return false;
	}

	bool _FindR(Node* root, const K& key)
	{
		if (root == nullptr)
			return false;

		if (root->_key < key)
			return _FindR(root->_right, key);
		else if (root->_key > key)
			return _FindR(root->_left, key);
		else
			return true;
	}

	void _InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}
private:
	Node* _root = nullptr;
};

四、二叉搜索树的应用

1.K模型：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到

的值。

2.KV模型：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。

 五、关于二叉树进阶面试题

 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    string tree2str(TreeNode* root) {
          if(root==nullptr)
            return string();
        string str;
        str+=to_string(root->val);
        //如果左子树不为空或者左右子树都不为空，左边需要加括号
        if(root->left||root->right)
        {
            str+='(';
            str+=tree2str(root->left);
            str+=')';
        }
        //右边如果不为空，右边需要加括号
        if(root->right)
        {
            str+='(';
            str+=tree2str(root->right);
            str+=')';
        }
        return str;
    }
};

 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        //如果此时二叉树为空，则返回vector<vector<int>>的匿名对象
        if(root==nullptr)
            return vector<vector<int>>();
        //利用队列先进先出的特性进行判断
        queue<TreeNode*> q;
        //利用二维数组来保存当前没一层的节点
        vector<vector<int>> vv;
        int levelSize=1;//每一行的节点数

        q.push(root);//将此时的根节点如队
        while(!q.empty())//如果队列不为空就继续
        {
           vector<int> v;
           for(int i=0;i<levelSize;i++)
           {
               TreeNode*front=q.front();//将队列的第一个数据保存然后出队
               q.pop();
               v.push_back(front->val);

               if(front->left)
                q.push(front->left);
               if(front->right)
                q.push(front->right);
           }
           levelSize=q.size();//将此时队列中的个数求出来
           vv.push_back(v);
        }
        return vv;
    }
};

 

 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
       //如果此时二叉树为空，则返回vector<vector<int>>的匿名对象
        if(root==nullptr)
            return vector<vector<int>>();
        //利用队列先进先出的特性进行判断
        queue<TreeNode*> q;
        //利用二维数组来保存当前没一层的节点
        vector<vector<int>> vv;
        int levelSize=1;//每一行的节点数

        q.push(root);//将此时的根节点如队
        while(!q.empty())//如果队列不为空就继续
        {
           vector<int> v;
           for(int i=0;i<levelSize;i++)
           {
               TreeNode*front=q.front();//将队列的第一个数据保存然后出队
               q.pop();
               v.push_back(front->val);

               if(front->left)
                q.push(front->left);
               if(front->right)
                q.push(front->right);
           }
           levelSize=q.size();//将此时队列中的个数求出来
           vv.push_back(v);
        }
        reverse(vv.begin(),vv.end());
        return vv;
    }
};

 

 

 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool Find(TreeNode*root,TreeNode*x,stack<TreeNode*>&path)
    {
        if(root==nullptr) return false;
        path.push(root);
        if(root==x) return true;
       

        //如果没有找到从左子树开始找，如果没找到去右子树中找，如果都没有找到此时需要将所有的当前节点需要进行出栈的操作
        if(Find(root->left,x,path)) return true;
        if(Find(root->right,x,path)) return true;
        
        path.pop();
        return false;

    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==nullptr)  return nullptr;
        
        //利用DFS来保存每一次搜索的路径
        stack<TreeNode*> pPath,qPath;

        Find(root,p,pPath);
        Find(root,q,qPath);

        //根据求两个链表公共节点的策略来求出二叉树中两个节点的最近的公共祖先的问题
        while(pPath.size()!=qPath.size())
        {
            if(pPath.size()>qPath.size()) pPath.pop();
            else qPath.pop();
        }

        while(pPath.top()!=qPath.top())
        {
            pPath.pop();
            qPath.pop();
        }
        return pPath.top();
    }
};

 

 

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
	void InOrderConvert(TreeNode*cur,TreeNode*&prev)
	{
		if(cur==nullptr) return;
		//先找出左子树
		InOrderConvert(cur->left,prev);
		cur->left=prev;
		if(prev)
			prev->right=cur;
		prev=cur;
		InOrderConvert(cur->right,prev);
	}
    TreeNode* Convert(TreeNode* pRootOfTree) {
		TreeNode*prev=nullptr;
		InOrderConvert(pRootOfTree,prev);

		while(pRootOfTree&&pRootOfTree->left)
			pRootOfTree=pRootOfTree->left;
		return pRootOfTree;
    }
};

 

 

 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //利用前序来创建树，中序来分割区间
    TreeNode*buildTreeHelper(vector<int>&preorder,vector<int>&inorder,int& prei,int inbegin,int inend)//这里previ需要利用引用，因为下一次递归prei会发生改变
    {
        if(inbegin>inend) return nullptr;
        TreeNode*root=new TreeNode(preorder[prei++]);
        
        //将中序的区间进行划分
        int ini=inbegin;
        while(ini<=inend)
        {
            if(inorder[ini]==root->val) break;
            else ++ini;
        }
        //利用分治法的思想继续分割左右区间
        root->left=buildTreeHelper(preorder,inorder,prei,inbegin,ini-1);
        root->right=buildTreeHelper(preorder,inorder,prei,ini+1,inend);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int i=0;
        return buildTreeHelper(preorder,inorder,i,0,inorder.size()-1);
    }
};

 

 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
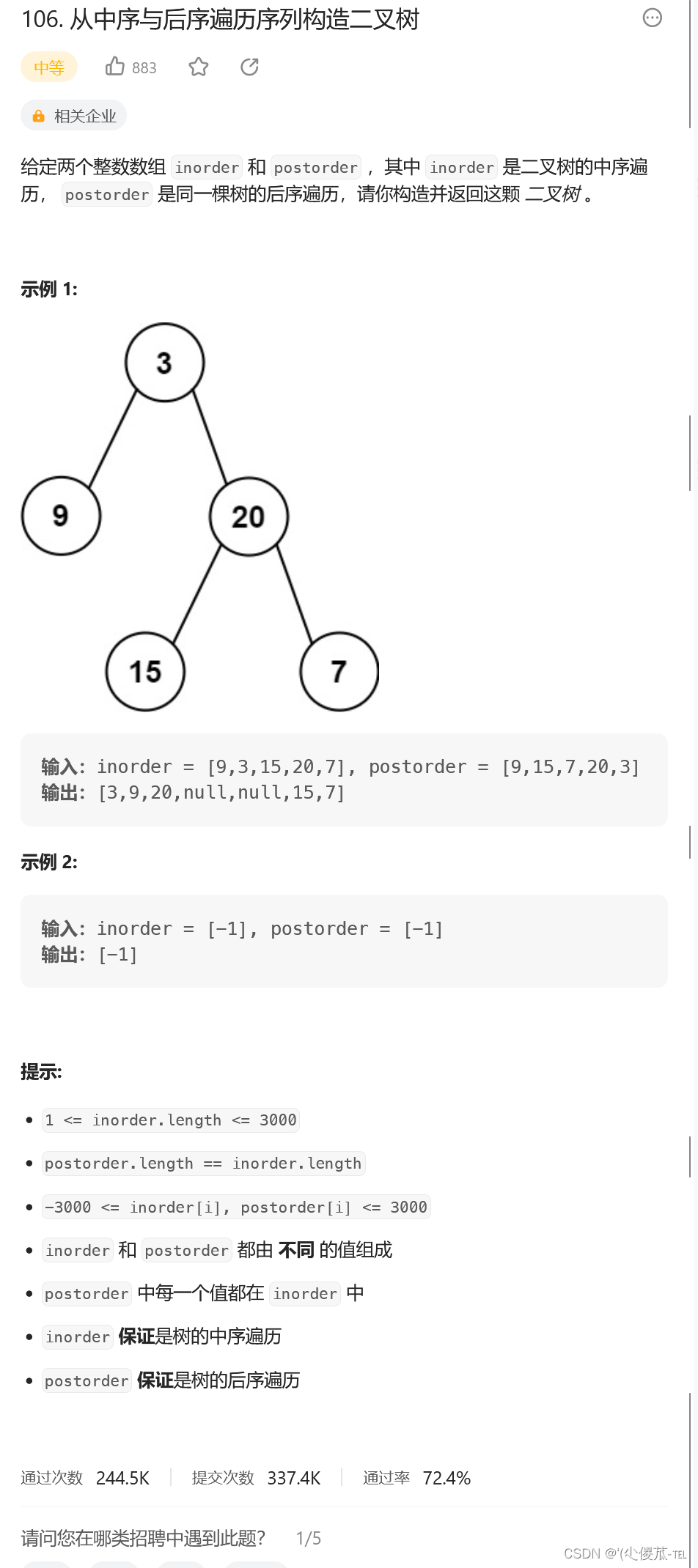
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {

    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        if(root==nullptr)
            return vector<int>();
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode*cur=root;

        while(cur||!st.empty())
        {
        //左路节点入栈
        while(cur)
        {
            v.push_back(cur->val);
            st.push(cur);

            cur=cur->left;
        }

        //右路节点的右子树
        TreeNode*top=st.top();
        st.pop();
        cur=top->right;
        }
    return v;
    }
  
};

 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
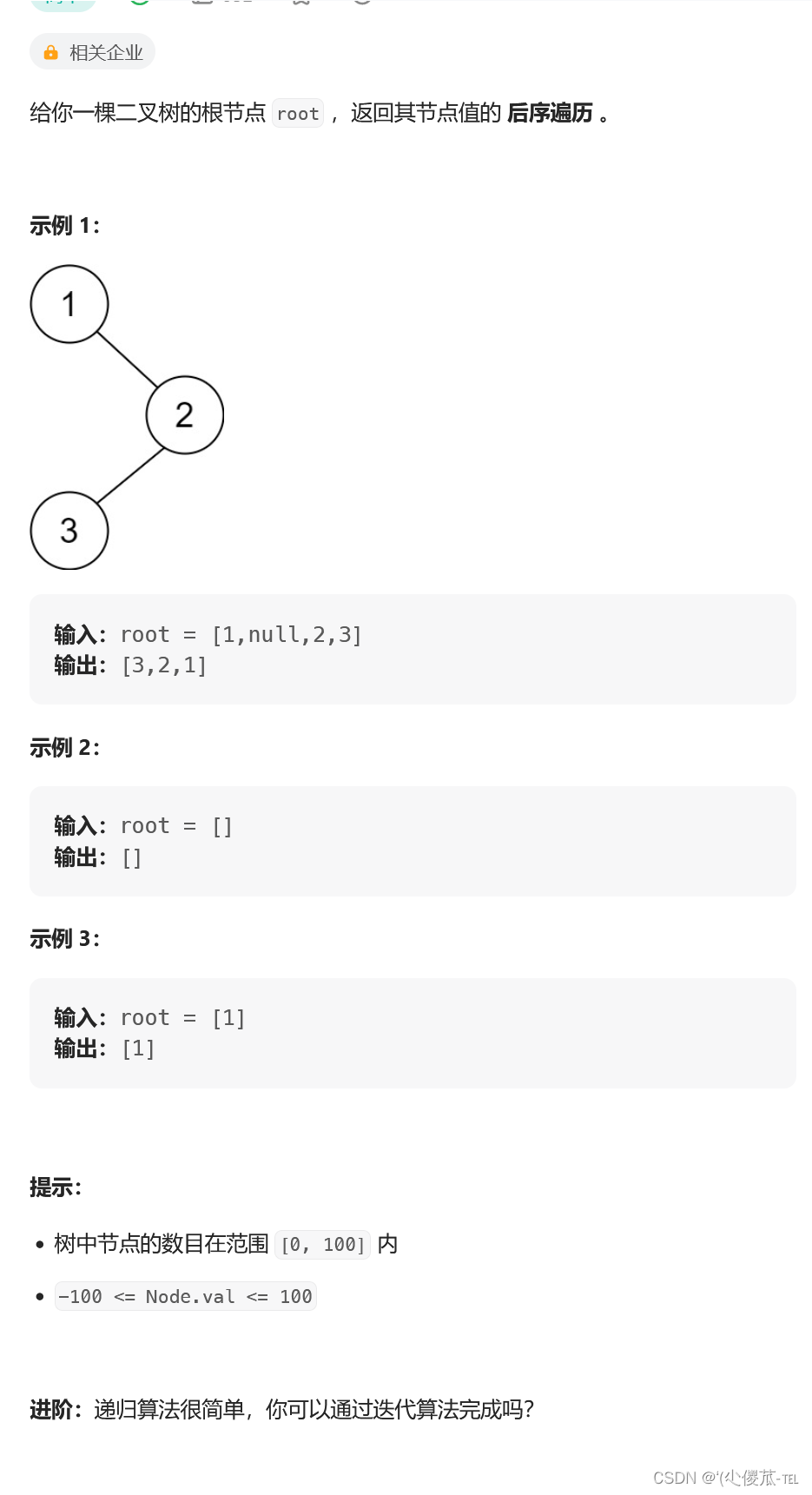
    vector<int> inorderTraversal(TreeNode* root) {
        if(root==nullptr)  return vector<int>();

        TreeNode*cur=root;
        stack<TreeNode*> st;
        vector<int> v;

        while(cur||!st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }

            TreeNode*top=st.top();
            v.push_back(top->val);
            st.pop();

            cur=top->right;
            
        }
        return v;
    }
};

 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        if(root==nullptr)  return vector<int>();

        TreeNode*cur=root;
        TreeNode*prev=nullptr;
        vector<int> v;
        stack<TreeNode*> st;

        //一个节点不为空的情况下：
        //右子树没有访问，访问右子树
        //右子树已经访问过了，访问根节点
        while(cur||!st.empty())
        {
            //左路节点入栈
            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }
            TreeNode*top=st.top();

            //右路节点
            //如果右为空或者没有访问过
            if(top->right==nullptr||top->right==prev) 
            {
                v.push_back(top->val);
                prev=top;
                st.pop();
            } 
            else
            {
                cur=top->right;
            }
        }
        return v;
    }
};

 

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/30490.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

大衣哥又有喜事了，孟文豪新作《克什克腾的眼泪》，是给他写的吗

大衣哥又有喜事了，孟文豪新作《克什克腾的眼泪》，是给他写的吗

农民歌唱家大衣哥又出新歌啦&#xff01; 就在大衣哥被谷传民起诉不久&#xff0c;互联网上面又传出新消息&#xff0c;继《火火的情怀》之后&#xff0c;大衣哥的新歌《新时代的新农民》&#xff0c;又要和大家见面了。很多人不明白&#xff0c;大衣哥不过是一个农民歌唱家&am…
阅读更多...
Java中的反射，枚举和Lambda表达式

Java中的反射，枚举和Lambda表达式

一. 反射 1. 反射的概述 2. 反射的使用 反射常用的类 通过反射获取Class对象 获得Class类相关的方法 使用反射创建实例对象 使用反射获取实例对象中的构造方法 通过反射获取实例对象的属性 通过反射获取实例对象的方法 3. 反射的优缺点 二. 枚举 1…
阅读更多...
Graalvm 安装和静态编译

Graalvm 安装和静态编译

文章目录1、下载2、graalvm安装3、native-image工具安装3.1 安装native-image3.2 安装C编译工具4、java编译成二进制exe4.1、普通的java命令行应用4.2、Swing应用编译4.3、使用maven插件静态编译4.4、javafx应用编译1、下载 文件下载&#xff1a;https://www.graalvm.org/down…
阅读更多...
[附源码]计算机毕业设计JAVA剧本杀门店管理系统-

[附源码]计算机毕业设计JAVA剧本杀门店管理系统-

[附源码]计算机毕业设计JAVA剧本杀门店管理系统- 项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM myb…
阅读更多...
OBS-VirtualCam OBS的虚拟摄像头插件

OBS-VirtualCam OBS的虚拟摄像头插件

OBS-VirtualCam 是OBS的一个虚拟摄像头插件&#xff0c;可以将OBS中的内容提供给一个虚拟摄像头&#xff0c;这样其它软件就可以使用这个内容了&#xff0c;这里试试这个插件功能。 1. 下载obs并安装 登录OBS Studio网站&#xff0c;下载windows版&#xff0c; 下载完成后并安装…
阅读更多...
栈的基本操作

栈的基本操作

目录 一、什么是栈&#xff1f; 二、用单链表实现栈 三、用顺序表数组实现栈 一、什么是栈&#xff1f; 栈&#xff08;stack&#xff09;是一个先进后出&#xff08;FILO-First In Last Out&#xff09;的有序列表。 主要方法&#xff1a;入栈&#xff08;push&#xff09;…
阅读更多...
SCA算法优化脉冲耦合神经网络的图像自动分割（Matlab代码实现）

SCA算法优化脉冲耦合神经网络的图像自动分割（Matlab代码实现）

&#x1f352;&#x1f352;&#x1f352;欢迎关注&#x1f308;&#x1f308;&#x1f308; &#x1f4dd;个人主页&#xff1a;我爱Matlab &#x1f44d;点赞➕评论➕收藏 养成习惯&#xff08;一键三连&#xff09;&#x1f33b;&#x1f33b;&#x1f33b; &#x1f34c;希…
阅读更多...
【C语言】初识指针（终篇）

【C语言】初识指针（终篇）

摸了一手秀发&#xff0c;发现还在~ 目录 1、指针运算 1.1指针加减整数 1.2指针减指针 1.3指针关系运算 2、二级指针 3、指针和数组 4、指针数组 前言&#xff1a; 大家好&#xff0c;我是拳击哥。上一期我们讲到了指针类型&#xff0c;指针的访问步长&#xff0c;野指针…
阅读更多...
Redis数据类型总结

Redis数据类型总结

文章目录一、5种数据类型二、常用指令汇总三、应用汇总提示&#xff1a;以下是本篇文章正文内容&#xff0c;Redis系列学习将会持续更新 一、5种数据类型 Redis 数据存储格式&#xff1a;  ● redis 自身是一个 Map ,其中所有的数据都是采用 key : value 的形式存储。  ● 数…
阅读更多...
如何设计用户体验测试用例

如何设计用户体验测试用例

一、 什么是用户体验 UE&#xff1a; User Experience 用户体验。 用户体验是指用户在使用产品过程中的个人主观感受&#xff0c;即用户在使用一个产品之前、使用过程中、使用后的整体感受&#xff0c;包括行为、情感、喜好、生理和心里反应、成就等各个方面。 通俗的讲用户体…
阅读更多...
希望所有计算机学生都知道这些宝藏网站

希望所有计算机学生都知道这些宝藏网站

GitHub GitHub是一个面向开源及私有软件项目的托管平台&#xff0c;因为只支持Git作为唯一的版本库格式进行托管&#xff0c;故名GitHub。 作为开源代码库以及版本控制系统&#xff0c;Github拥有超过900万开发者用户。随着越来越多的应用程序转移到了云上&#xff0c;Github已…
阅读更多...
数据结构与算法(五) 动态规划

数据结构与算法(五) 动态规划

这篇文章来讲动态规划&#xff08;Dynamic Programming&#xff09;&#xff0c;这是一个在面试中很经常出现的题型 1、本质 之前说过&#xff0c;解决算法问题的主流思路就是穷举搜索&#xff0c;即遍历整个搜索空间&#xff0c;找到给定问题的解 只是在某些场景下&#xff…
阅读更多...
Python学习 - 异常处理

Python学习 - 异常处理

Python学习 - 语法入门&#xff1a;https://blog.csdn.net/wanzijy/article/details/125287855 Python学习 - 数据类型&#xff1a;https://blog.csdn.net/wanzijy/article/details/125341568 Python学习 - 流程控制&#xff1a;https://blog.csdn.net/wanzijy/article/details…
阅读更多...
3dmax网渲云渲染哪个平台费用低？一张图要多少钱多长时间？怎么收费

3dmax网渲云渲染哪个平台费用低？一张图要多少钱多长时间？怎么收费

话说现在的设计师应该没有不知道云渲染的吧&#xff1f;毕竟比起本地渲&#xff0c;云渲染不占本地资源&#xff0c;一次能渲很多张&#xff0c;方便又快捷&#xff0c;有谁不喜欢呢&#xff01;那么这么多的云渲染平台用哪个呢&#xff1f;今天我们就以主流的4个平台为例&…
阅读更多...
(STM32)从零开始的RT-Thread之旅--SPI驱动ST7735(4)使用LVGL

(STM32)从零开始的RT-Thread之旅--SPI驱动ST7735(4)使用LVGL

上一篇&#xff1a; (STM32)从零开始的RT-Thread之旅--SPI驱动ST7735(3)使用DMA 经过前几章的搭建&#xff0c;底层显示已经没有问题了&#xff0c;现在需要添加上层的库&#xff0c;我选择了比较火的开源GUI库--LVGL。而RT-Thread Studio支持直接添加LVGL代码库的。 在RT-T…
阅读更多...
人工智能-4计算机视觉和图像处理01

人工智能-4计算机视觉和图像处理01

深度学习简介 机器学习是实现人工智能的一种途径&#xff0c;深度学习是机器学习的一个子集 深度学习相比于机器学习&#xff0c;少了‘手动特征提取’部分&#xff0c;交给网络来处理 深度学习流程&#xff1a;数据输入–训练模型&#xff08;在数据中学习&#xff09;–输出预…
阅读更多...
IP请求工具

IP请求工具

无缝的 IP 分配和管理 手动将不同子网中的 IP 分配给不同的 IT 管理员&#xff0c;同时遵守配置的不同访问级别可能是一项繁琐的任务。为了简化IP请求和分配的过程&#xff0c;OpUtils为您提供了一个内置的IP请求工具。使用此工具&#xff0c;您的网络管理员不必再等待其 IP 请…
阅读更多...
数据库笔记

数据库笔记

文章目录01 数据库概述1.1 四个基本概念1.2 数据管理技术的三个阶段1.2.1 人工管理阶段1.2.2 文件系统阶段1.2.3 数据库阶段1.3 数据独立性1.4 数据库的三级模式结构1.4.1 三级模式结构1.4.2 数据库的二级映像与数据独立性02 关系数据库2.1 关系数据结构及形式化定义2.1.1 关系…
阅读更多...
论文管理系统(增删查改功能的实现)

论文管理系统(增删查改功能的实现)

目录 一、后端 1.1实体类 1.2paperMapper类 1.3 PaperMapper类 1.4Service层 1.5 Controller层 二、前端 源代码 我们已经实现列表数据了,接下来我们将实现增删查改功能,新增和修改还能够回显 一、后端 1.1实体类 实体类还是我们上一版的列表功能的实现的paper实…
阅读更多...
IFD-x 微型红外成像仪探测距离说明

IFD-x 微型红外成像仪探测距离说明

红外热成像仪是用光学镜头来收集被测物体的热辐射能量的&#xff0c;故此探测距离会受镜头视场角 和热成像像素分辨率有关。 假如某成像仪的成像分辨率为 32*32 像素&#xff0c;视场角为 75 度&#xff0c;则可以理解为从镜头发射出 32*321024 条激光来探测 1024 个点的…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023