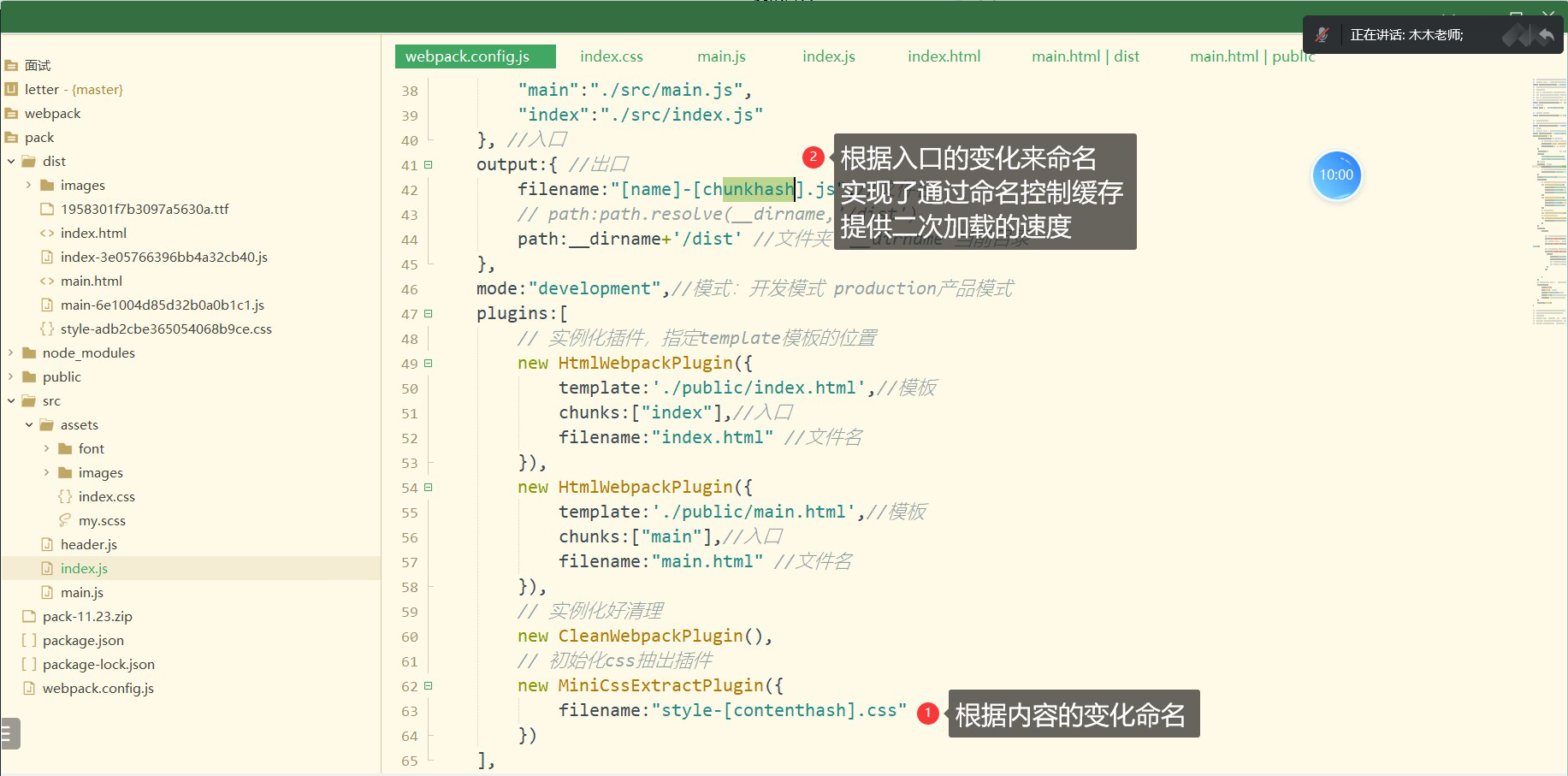
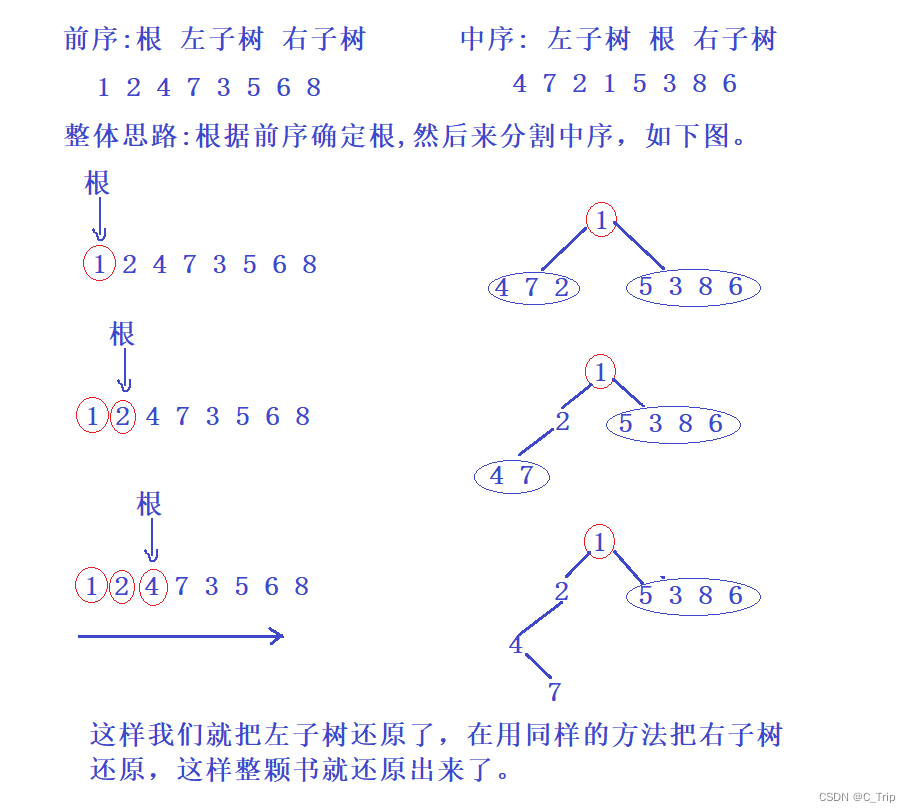
Fast Color Segementation 发表于CVPR 2020，主要是对之前的一篇图像软分割的论文（参见：论文回顾：Unmixing-Based Soft Color Segmentation for Image Manipulation，Aksoy 2017）进行改进。

一、论文简介

[Aksoy 2017] 这篇论文假设每个图层的颜色服从一个正态分布，并通过优化的方法求解每个图层的均值，协方差矩阵，以及不透明度。总体上效率低下，难以满足实时性的需求，因此，本文通过深度学习的方法快速的预测半透明的图层。

先来看一下论文的teaser。输入：原始图像 + 调色板， 输出：RGBA图层，应用主要就是图像重着色。

二、本文解决方案

本文给出的网络结构主要基于AutoEncoder结构，如下所示，主要包括3个模块：调色板提取（Palatte Seletion），不透明度预测（Alpha Layer Estimation）和 RGBA图层预测 Color Layer Estimation。

1）调色板提取

调色板提取主要通过K-means算法对图像聚类获取，K的数目是固定的。预测过程中，调色板的颜色也可由用户直接指定。

2）不透明度预测

使用U-net网络预测每一个图层的不透明度（每个图层任意像素位置均有一个不透明度）.
输入：原始图像 $I$ + 调色板 U = { u 1 , u 2 , . . . u K } U=\{u_1,u_2,...u_K\} U={u1​,u2​,...uK​}。
输出：K个跟原始图像尺寸相同的不透明度图层（单通道，取值位于[0,1]）， A = { α 1 , α 2 , . . . α K } A=\{\alpha_1,\alpha_2,...\alpha_K\} A={α1​,α2​,...αK​}。

通过归一化操作，使得图层在任意位置的取值位于[0,1]。为了使得重建误差尽可能小，这一部分的损失函数定义为：
$$L_r=\sum _{p\in I}|\sum _{i=1}^K{\alpha }_i^p{u}_i-c^p|\text{\hspace{1em}(1)}$$

其中，$p$ 表示图像中任意像素的位置，${\alpha }_i^p$ 表示第 $i$ 个图层 在 $p$ 点处的不透明度。${\sum }_{i=1}^K{\alpha }_i^p{u}_i$ 表示经多个图层重建的颜色，$c^p$表示输入图像在$p$点处的颜色。

3）图层颜色微调

[Tan 2016] 使用凸包作为图像调色板，然后通过广义中心坐标插值算法计算的权重，可以很完美的重建输入图像。 本质上是因为凸包在几何上具有很好的性质，即凸包内部的任意点可以被凸包顶点唯一的表示为凸包顶点的线性组合（凸组合），从而保证了精确的重建。然而本文使用聚类的算法提取的调色板颜色并不具备这样的性质，因此难以通过插值实现精确的重建。

为了实现精确的重建，本文进一步对调色板进行改进，对单色的调色板进行扰动，变成非单色的调色板。其实差不多就是[Aksoy 2017] 的思想，只不过[Aksoy 2017] 假设每一个图层的RGB服从正态分布，本文并没有这么强的约束。

这里使用U-net预测图层颜色的变化量。
输入：原始图像 + 调色板 + 上一步计算出的图层不透明度
输出：调色板颜色的变化量 △ U = { △ u 1 , △ u 2 , . . . △ u K } \triangle U = \{\triangle u_1,\triangle u_2,...\triangle u_K\} △U={△u1​,△u2​,...△uK​}

上图所示的：

• RGB layers: G = [ U = { u 1 , u 2 , . . . u K } ] + [ △ U = { △ u 1 , △ u 2 , . . . △ u K } ] G = [U=\{u_1,u_2,...u_K\}] +[ \triangle U = \{\triangle u_1,\triangle u_2,...\triangle u_K\}] G=[U={u1​,u2​,...uK​}]+[△U={△u1​,△u2​,...△uK​}], 这样一来，调色板的颜色确实不再是单色。
• Decomposed layers 其实就是 三通道的 RGB layer + 单通道的不透明度，结果为四通道的RGBA 图层。

这一部分的损失函数包块两部分：

1） 通过非单色调色板$P$ 和 不透明度的重建损失定义为：
$$L_{\alpha }=\sum _{p\in I}|\sum _{i=1}^K{\alpha }_i^p{G}_i^p-c^p|\text{\hspace{1em}(2)}$$
其中，$G_i^p$ 表示第 $i$ 个非单色调色板在 $p$ 处的颜色，其他跟第一个损失函数类似。

2）我们期望 $G$ 应当尽可能趋近 $U$, 也就是尽可能单色，只是局部有些扰动。因此，添加额外约束。
$$L_d=\sum _{p\in I}|\sum _{i=1}^K{G}_i^p-u_i^p|\text{\hspace{1em}(3)}$$

整体损失函数定义为：
$$L_{total}=L_r+L_{\alpha }+L_d\text{\hspace{1em}(4)}$$

这就是这个网络的全部内容了。

三、实验

• 1. 跟[Aksoy 2017]的比较如下所示，可以看出图层结果十分接近。

• 2. 运行时间对比，可以看出本文算法在速度上具有非常明显的优势

• 

四、简单总结

本文通过深度学习的方法根据已有的调色板，预测不透明度，并对原始调色板进行微调，使得重建图像具有较小的误差。跟已有算法相比极大的提升了速度。缺点跟之前的算法一样，因为得到的调色板已经不是单色，所以编辑起来并不容易，需要借助PS软件对RGBA图层单独编辑。