Problem - 1689C - Codeforces

Byteland是一片美丽的土地，因其美丽的树木而闻名。

米沙发现了一棵有n个顶点的二叉树，编号从1到n。二叉树是一个无环连接的双向图，包含n个顶点和n-1条边。每个顶点的度数最多为3，而根是数字为1的顶点，它的度数最多为2。

不幸的是，根部被感染了。

下面的过程会发生N次。

Misha要么选择一个没有被感染（也没有被删除）的顶点，并删除它和所有以这个顶点为终点的边，要么就什么都不做。
然后，感染扩散到每个与已经被感染的顶点相连的边的顶点（所有已经被感染的顶点仍然被感染）。
由于Misha没有太多时间考虑，请告诉他他能从感染中救出的顶点的最大数量（注意，删除的顶点不计入救出的顶点）。

输入
在输入数据中，有几个测试案例。第一行包含一个整数t（1≤t≤5000）--测试案例的数量。接下来是测试用例的描述。

每个测试用例的第一行包含一个整数n（2≤n≤3⋅105）--树的顶点数量。

测试用例中接下来的n-1行中的第i行包含两个正整数ui和vi（1≤ui,vi≤n），意味着在图中它们之间存在一条边。

保证该图是一棵以1为根的二叉树，也保证所有测试案例的n之和不超过3⋅105。

输出
对于每个测试案例，输出Misha可以保存的最大顶点数量。

题解:
由于从根部开始进行感染,如果这个根有左右节点,那么那么我们会切除其中一个,但是另一个会被继续感染,那么这种情况到什么时候结束呢,

有两种情况

1.出现叶子节点(没有后续节点的点),我们肯定会删除不是叶子节点的点,到此结束

2.出现单分支节点,类似

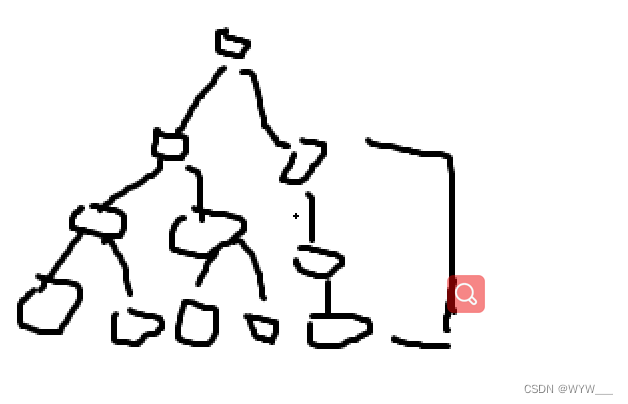
这种情况下我们切除被感染的下一个节点,到此结束

如果理解了上面的分析相信大家就能看到，每经过一秒，就会有两个结点牺牲，直到遇到单分支结点或者叶子结点为止，

如果遇到单分支结点，最后就是单分支的孩子结点被砍，

而如果是叶子结点，那么最后就是叶子结点被感染，

通过这样的分析，大家肯定能发现每经过一秒牺牲的结点所在的层次数就会+1，直到遇到上面两种情况为止，所以题目就转化为求出距离根节点最近的叶子结点或者是单分支结点，

如果距离根节点的最近结点是叶子结点，那么牺牲的结点数就是叶子结点所在的层数*2-1，

而如果距离根节点的最近结点是单分支结点，那么牺牲的结点数就是单分支结点所在层数*2，答案就是总结点个数减去牺牲的结点个数即可。

 注意根节点由于没有父节点，所以他的出边要比正常结点少1，所以需要特殊判断一下。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<map>
#include<vector>
#include<queue>
using namespace std;
#define int long long
//1 1 3 3 3
int n,ans;
vector<int> p[300050];
void dfs(int x,int fa,int d)
{
	if(p[x].size() == 2&&x != 1)
	{
		ans = max(ans,n - 2*d);
	}
	else if(p[x].size() == 1)
	{
		if(x == 1)
		{
			ans = max(ans,n - 2);
		}
		else
		{
			ans = max(ans,n - (2*d-1));
		}
	}
	for(int i = 0;i < p[x].size();i++)
	{
		int j = p[x][i];
		if(j == fa)
		continue;
		dfs(j,x,d+1);
	}
}
void solve()
{
	cin >> n;
	for(int i = 1;i <= n;i++)
	p[i].clear();
	for(int i = 1;i <n;i++)
	{
		int l,r;
		cin >> l >>r;
		p[l].push_back(r);
		p[r].push_back(l);
	}
	ans = 0;
	dfs(1,-1,1);
	cout<<ans<<"\n";
}
signed main()
{
	int t = 1;
	cin >> t;
	while(t--)
	{
		solve();
	}
}
//2 5
//3
//9 7 


//2  3 4 3
//1 2 3 4 5
//      3