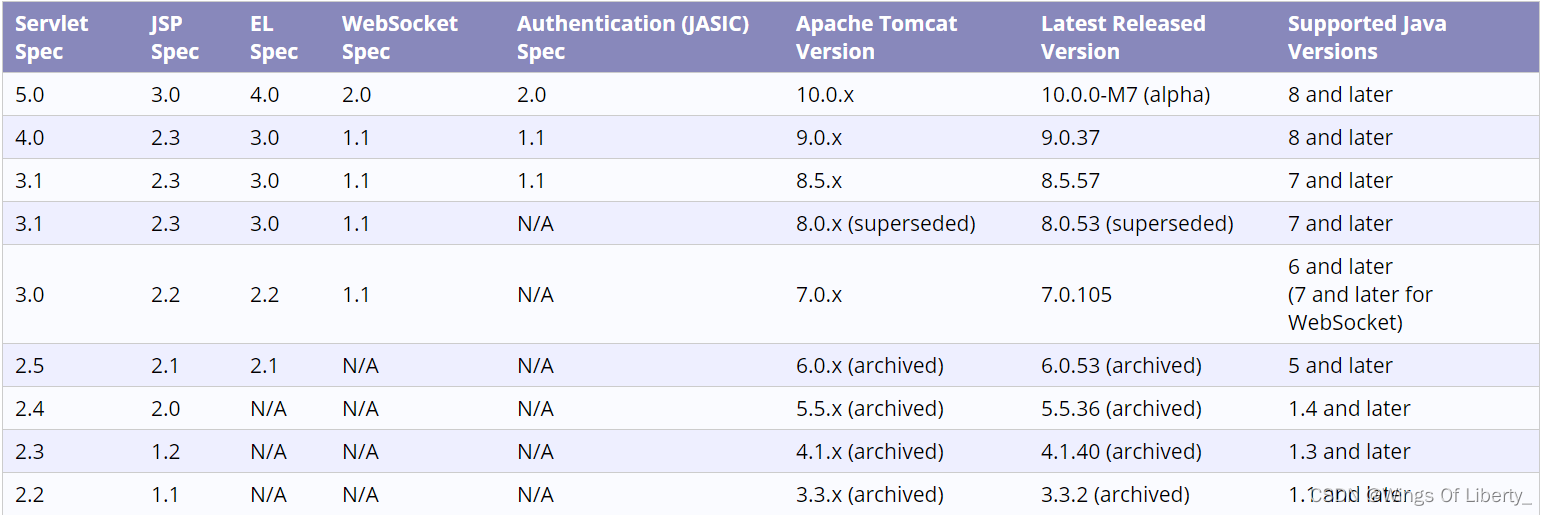
目录

一、差分简介

一维差分结论

Acwing.797 差分

P4552 [Poetize6] IncDec Sequence - 差分思维玄学题

---

一、差分简介

• 规定a数组下标从1开始  a[0]=0
• b数组下标从1开始
• 定义一个数组b，使 
• 对于a数组              
• 其差分数组b为       
• a是b的前缀和数组  
• 比如  a[2] = b[1]+b[2] = 4+4= 8
• 比如  a[4] = b[1]+b[2]+b[3]+b[4] = 4+4-2-1 = 5

•  如果我们要给a数组【l , r】区间都+c   即 a[l]+c , a[l+1]+c …… a[r]+c

• 首先给 b[l]+c 则    

• 然后给 b[r+1] - c 则   

先给b[l]+c 则a数组的红色区域都会+c

再给b[r+1]-c 则a数组的绿色区域都会-c

从而达到只给区间 [l,r]+c 的目的

一维差分结论

给a数组 [l,r] 区间的每个数+c，只需要给其差分数组b做如下操作即可

b[l]+=c;
b[r+1]-=c;

Acwing.797 差分

 活动 - AcWing

import java.util.*;

public class Main
{
    static int N=(int)1e5+10;
    
    public static void main(String[] args)
    {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt(),k=sc.nextInt();
        int[] a=new int[N];
        int[] b=new int[N];
        for(int i=1;i<=n;i++)
        {
            a[i]=sc.nextInt();
            b[i]=a[i]-a[i-1]; //构造差分数组
        }
        int l,r,c;
        while(k-->0)
        {
            l=sc.nextInt();
            r=sc.nextInt();
            c=sc.nextInt();
            b[l]+=c;
            b[r+1]-=c;
        }
        for(int i=1;i<=n;i++)
        {
            a[i]=a[i-1]+b[i]; //b的前缀和是a
            System.out.print(a[i]+" ");
        }
    }
}

P4552 [Poetize6] IncDec Sequence - 差分思维玄学题

[Poetize6] IncDec Sequence - 洛谷

思路：

这题可以转化为求出原数列的差分数组b，最后使得 

题目中对数组a的操作，相当于每次能选出  中任意两个数，一个+1，一个-1

• x= b中所有正数之和
• y= b中所有负数之和的绝对值
• 我们需要先正负抵消，这时剩下最后一个数，再单独把这个数消成0
• 所以操作数就是 max(x,y)

• 求方案数 也就是求的可能数
• 完成以上操作后得到的b差分数组就是 
• 要把 x-y 消0，需要  步
• 所以b[1]会有  种方案

#include <bits/stdc++.h>
using namespace std;

const int N=1e5+10;
long long a[N],zheng,fu;

int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=2;i<=n;i++)
    {
        int x=a[i]-a[i-1];
        if(x>0) zheng+=x;
        else fu+=abs(x);
    }
    cout<<max(zheng,fu)<<endl<<abs(zheng-fu)+1;
    return 0;
}