蓝桥杯题库

一.等差素数列（较难）

这道题有公式，其等差就是它长度内所有素数的乘积，也就是2 * 3 * 5 * 7

当然我们基本上不会看到这种公式，所以如果用程序来写的话，我们使用枚举法

int is_prime(int i)
{
    int j = 0;
    for (j = 2; j < i / 2; j++)
    {
        if (i % j == 0)
        {
            return 0;
        }
    }
    return 1;
}

int main()
{
    int i = 0, n = 0;
    for (i = 2; i < 10000; i++)//枚举从2到10000的数字
    {
        if (is_prime(i))//如果第一个是素数
        {
            for (n = 2; n < 1000; n++)//枚举等差的值
            {
                int k = 0;//这是后面的个数
                while (is_prime(i + n * k))//如果该素数加上一个等差值依然是素数就继续
                {
                    k++;
                }
                if (k == 10)//如果该素数一直加了10个n依然是素数，就说明他的长度是10
                {
                    printf("%d", n);
                    return 0;//这里直接退出main函数
                }
            }
        }
    }
    return 0;
}

二.货物摆放（思路新奇）

这道题其实就是判断三个数出现组合次数

我们先不区分长宽高，单单从有哪些数相乘的积是n来看

我们令i是那个较小数，j是那个较大数，k是那个最大数

#include<stdio.h>
int main()
{
    long long n=2021041820210418;
    long long k,s,sum=0;
    for(long long i=1;i*i*i<=n;i++)//由于i是最小的，那么它最大为三次根号下n
    {
        if(n%i==0)//如果i是n的一个因数
        {
            s=n/i;//剩下是k和j的乘积
            for(long long j=i;j*j<=s;j++)//由于j是j和k中小的，那么j最大可达到开根号s
            {
                if(s%j==0)//如果j是s的因数（也是n的第二个因数）
                {
                    k=n/i/j;
                    //以下进行排序
                    if(i==j&&i==k)//如果三个因数全部相等（例如3，3，3），那么只有一种排序
                        sum++;
                    else if(i==j&&i!=k)//如果有两个因数相等（例如1，3，3），那么有三种排序
                        sum+=3;
                    else  //如果三个因数都不相等（例如1，2，3）那么有六种排序
                        sum+=6;
                }
            }
        }
    }
    printf("%d",sum);
    return 0;
}

三.既约分数

这道题其实就是求两个数是不是互为素数，这里主要考察的是如何求最大公约数，我在这用的是辗转相除法

#include<stdio.h>
int Gcd(int a,int b)
{
	if(a > b)
	{
		if(a % b == 0)
		{
			return b;
		}
		else
		{
			return Gcd(b,a%b);    
		}
	}
	else
	{
		if(b % a == 0)
		{
			return a;
		}
		else
		{
			return Gcd(a,b%a);
		}
	}
}

int main()
{
  int count=0;
  for(int i=1;i<=2020;i++)
  {
    for(int j=1;j<=2020;j++)
    {
      if(Gcd(i,j)==1)
      {
        count++;
      }
    }
  }
  printf("%d",count);
  return 0;
}

辗转相除法如果不会可以去网上搜，很多讲解，这里就不介绍啦

四.跳跃

这道题如果用图表示出来的话

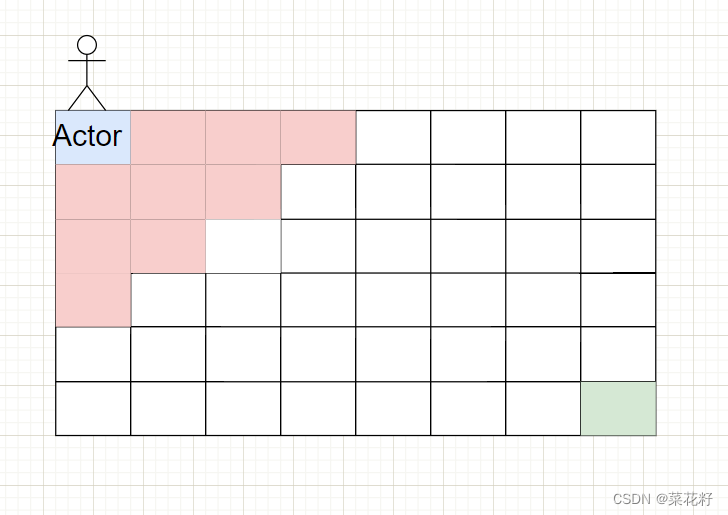
其实就是判断这九个格子的最大值，然后赋值

#include <stdio.h>
int b[105][105];//每个点的权值
int find_max(int x,int y)
{
  int max=0;
  for(int i=x;i>=1;i--)
  {//从下往上倒推
    for(int j=y;j>=1;j--)
    {//从右往左倒推
      if(!(x==i&&y==j)&&(x-i+y-j)<=3&&max<b[i][j]){
        //同时满足三个条件
        //1.不原地踏步2.每次跳跃在距离范围之内3.比当前max更大时才更新max
        max=b[i][j];
      }
    }
  }
  return max;
}
int main(){
  int n,m;
  scanf("%d %d",&n,&m);
  int i,j;
  for(i=1;i<=n;i++)
  {
    for(j=1;j<=m;j++)
    {
      scanf("%d",&b[i][j]);
    }
  }
  for(i=1;i<=n;i++)
  {
    for(j=1;j<=m;j++)
    {
      b[i][j]+=find_max(i,j);
    }
  }
  printf("%d",b[n][m]+b[1][1]);//最后一个元素加之前所有权重的最大值
  return 0;
}

五.数值求值（坑题）

这道题说实话让我一言难尽，其实很简单，但它就坑在数值太大

如果数值正常，我们可以如下写

#include <stdio.h>
int main(void)
{
  int a=1,b=1,c=1,d,i;
  for(i=4;i<=20190324;i++)
  {
    d=a+b+c;//a为第一项，b为第二项，c为第三项，d为第四项，d=前三项和
    a=b;//将第二项值给第一项
    b=c;//将第三项值给第二项
    c=d;//将第四项值给第三项
  }
  printf("%d",d);
  return 0;
}

这其实就是一个斐波那契数列，但我提交时怎么也过不了，因为这个数值太大了，无论是long还是longlong都存不下，这就很坑了，那我们只能如下写

#include <stdio.h>
int main(void)
{
  int a=1,b=1,c=1,d,i;
  for(i=4;i<=20190324;i++)
  {
    d=(a+b+c)%10000;//题目要求我们只取最后四位 ， 那我们可以对每次运算出来的结果 %10000 这样每次结果就都保留最后四位数字
    a=b;
    b=c;
    c=d;
  }
  printf("%04d",d);
  return 0;
}