代码随想录算法训练营第八天|二叉树（截止到左叶子之和）

翻转二叉树

Leecode 226.翻转二叉树

链接：https://leetcode.cn/problems/invert-binary-tree/

用递归来做，若是遇到空节点，直接return

然后交换左右节点，接着递归

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == NULL) return root;
        swap(root->left, root->right);  // 中
        invertTree(root->left);         // 左
        invertTree(root->right);        // 右
        return root;
    }
};

对称二叉树

Leecode 101. 对称二叉树

链接：https://leetcode.cn/problems/symmetric-tree/

本来的想法是：用层序遍历的方法得到每层的vector后check其是不是回文，若是回文则对称，但是这种方法遇到示例2直接就死了

所以我们要换一种思路：不单单是记录每一层的节点，而是具体到左右节点去判断

例如当前如果左节点为空右节点不为空或者右节点为空左节点不为空，那么肯定是不符合题意的情况

先写出递归的四种终止条件

左空右不空 – false
左不空右空 – false
左空右空 – true
左不空右不空值不同 – false

然后我们在下面继续递归当前节点的左节点和右节点，别忘了用变量接住返回值

最后只有左子树和右子树的返回值都是true的时候才合法

 // 不要想层序遍历了好不好，二叉树的核心操作是递归啊！！！
// 递归的时候需要有值来接住返回值
class Solution {
public:
    bool check(TreeNode* l,TreeNode* r)
    {
        // 现在开始排除情况，若是左节点为空，右节点不空，或者是左节点空，右节点不空，那么绝对是不对称的
        if(l == NULL && r != NULL) return false;
        if(l != NULL && r == NULL) return false;
        if(l == NULL && r == NULL) return true;
        if(l -> val != r->val)     return false;
        bool left  =  check(l->left,r->right);
        bool right =  check(l->right,r->left);
        return left&&right;

    }
    bool isSymmetric(TreeNode* root) {
        if(root == NULL) return true;
        return check(root->left,root->right);
    }
};

二叉树的深度

Leecode104. 二叉树的最大深度

链接：https://leetcode.cn/problems/maximum-depth-of-binary-tree/

我们要分清用递归实现前序遍历和后序遍历的区别

这里给出递归实现层序遍历的代码

class Solution {
public:
    void order(TreeNode* cur, vector<vector<int>>& result, int depth)
    {
        if (cur == nullptr) return;
        //---------------------------------------------------//
        if (result.size() == depth) result.push_back(vector<int>());
        result[depth].push_back(cur->val);
        //---------------------------------------------------//
        order(cur->left, result, depth + 1);
        order(cur->right, result, depth + 1);
    }
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        int depth = 0;
        order(root, result, depth);
        return result;
    }
};

关键代码已经用注释框出，也就是我们用递归“逐层下降”的时候，就用vector记录了每层的值，所以这是前序遍历

那么如何用递归实现后序遍历呢？

就是遇见NULL或者return的时候才记录值，此时记录到的值一定是从下往上的，因此是后序遍历

class Solution {
public:
    int getdepth(TreeNode *head,int depth)
    {
        if(head == NULL) return depth;
        int dep1 = getdepth(head -> left,depth+1);
        int dep2 = getdepth(head -> right,depth+1);

        return max(dep1,dep2);
    }
    int maxDepth(TreeNode* root) {
        int depth = 0;
        if(root == NULL) return 0;
        int maxx = getdepth(root,0);  // 刚开始传入的是一个结点吧，每次每次递归判断的都是一个结点
        return maxx;
    }
};

代码所示，就是后序遍历

Leecode 111. 二叉树的最小深度

链接：https://leetcode.cn/problems/minimum-depth-of-binary-tree/

首先我们要明白深度的定义：当前节点的深度就是当前节点到叶子节点的距离

我当时做这道题的时候直接就是改了求最大深度的代码中的max，将其改成min

class Solution {
public:
    int get_minn_dep(TreeNode *head,int depth)
    {
        // 这句话是不可以省略的，不然肯定会空指针
        // 我们已经知道：当左子树为空右子树不为空的时候，左子树的返回值不是最小值，同理右子树为空左子树不为空的时候右子树返回的也不是最小值
        // 那么我们在哪里处理这两种情况呢？——当前是当前节点不为空的时候才可以做判断
        // 那么什么时候才知道当前节点不为空呢？计算了l_dep和r_dep后面···
        if(head == NULL) return depth;
        int l_dep = get_minn_dep(head -> left, depth+1);
        int r_dep = get_minn_dep(head -> right,depth+1);
		
        // if(head -> left == NULL && head -> right!=NULL) l_dep = r_dep;
        // if(head -> left != NULL && head -> right==NULL) r_dep = l_dep;
        return min(l_dep,r_dep);
    }
    int minDepth(TreeNode* root) {
        if(root == NULL) return 0;
        int res = get_minn_dep(root,0);
        return res;
    }
};

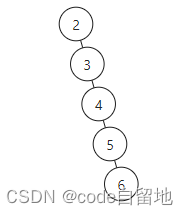
在这里插入图片描述

结果发现我们样例都过不了，仔细分析，发现对于这种形状的树（每个节点只有右儿子），按照上面代码来跑，结果是1而不是5

显然root节点的左儿子为空，所以返回的最小深度是1，这肯定是错误的，所以我们还要加上两句（也就是注释了的两句）：

若左节点为空，而右节点不为空，得到的左节点的深度就等于右节点的深度

若右节点为空，而左节点不为空，得到的右节点的深度就等于左节点的深度

完全二叉树

Leecode 222. 完全二叉树的节点个数

链接：https://leetcode.cn/problems/count-complete-tree-nodes/

可以用对付普通二叉树的方法做，也可以利用完全二叉树的性质做

// 普通方式
class Solution {
public:
    int cal(TreeNode *head)
    {
        if(head == NULL) return 0;
        int l_sum = cal(head->left);
        int r_sum = cal(head->right);

        return 1 + l_sum + r_sum;
    }
    int countNodes(TreeNode* root) {
        if(root == NULL) return 0;
        int num = cal(root);
        return num; 
    }
};

那么完全二叉树的性质是什么？

左子树的深度 = 右子树的深度

若是满足这个性质，那么整棵树的节点数量（包含根节点）就是(2 << 深度) - 1

// 利用完全二叉树的性质
class Solution {
public:
    int countNodes(TreeNode* root) {
        // 如果是空的话直接返回
        if(root == NULL) return 0;
        // 然后我们分别定义出左节点和右节点
        TreeNode* left  = root->left;
        TreeNode* right = root->right;

        int l_num = 0;
        int r_num = 0;

        while(left!= NULL)
        {
            left  = left->left;
            l_num ++;
        } 

        while(right!= NULL)
        {
            right  = right->right;
            r_num ++;
        } 

        if(l_num == r_num) return ((2 << l_num) - 1); // 如果当前子树有三层，那么一共是7个节点

        return countNodes(root -> left) + countNodes(root -> right) + 1;
    }
};

平衡二叉树

Leecode 110. 平衡二叉树

首先看平衡二叉树的定义：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1

显然，如果我们再遍历树的时候，遇到了不符合题意的情况，就要直接返回-1

之前做的题目都是累加深度，这是值得注意的一点

那么若是符合平衡二叉树呢？父节点的深度还要累加子节点的深度

所以正常满足平衡二叉树的定义时，我们就要返回当前节点的最大深度

接下来我们思考递归怎么写？

函数的返回值是int

若是空节点，我们就返回0

下面我们分别遍历左右子树，并用变量接住返回值

若是左右子树中有一个返回-1，那么最后返回的就是-1

否则，我们返回左右子树的最大深度+1

class Solution {
public:
    int check(TreeNode *head)
    {
        if(head == NULL) return 0;
        int l_num = check(head -> left);
        int r_num = check(head -> right);
        // 那如果左右都是-1呢？那不就寄了吗，所以左右返回值还需要判断，如果左右返回值有一个是-1，那么直接返回-1
        if(l_num == -1 || r_num == -1) return -1;
        if(abs(l_num - r_num) > 1) return -1;
        return max(l_num,r_num) + 1;

        // 返回值是什么，若是满足平衡二叉树，那么就返回当前节点的深度，若不是平衡二叉树，那么就返回-1
    }
    bool isBalanced(TreeNode* root) {
        if(root == NULL) return true;
        int res = check(root);
        if(res == -1) return false;
        return true;
    }
};

二叉树的所有路径

Leecode 257. 二叉树的所有路径

链接：https://leetcode.cn/problems/binary-tree-paths/
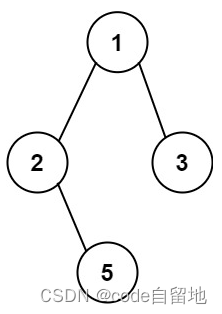
在这里插入图片描述

拿上图举例：我们不仅要输出[1->2->5]，还要输出[1->3]

显然根节点出现了两次，显然是需要回溯操作的

那么什么时候回溯呢？取决于我们记录到哪些元素，不像之前我们遇到了空节点才return，因为我们要记录所有节点，而且还是从上到下记录，因此我们不能return后再记录，而是向下遍历一层记录一次，也就是前序遍历。那么可以遍历到空节点吗？显然不行，因此return条件我们需要改一下，将其改成——遇到子节点（左右节点都为空）的时候才return，return之前，我们记录当前vector中记录到的所有节点并将其生成一条路径

返回条件改变，自然我们遍历的时候也不能随意指向，一定要是保证左右儿子存在的时候才往下遍历

那么回溯操作体现在哪里呢？自然是上面函数return了之后，当前函数的执行位置就是我们“往下遍历”的语句下面，我们需要回溯

孙哥给了一种写法，为了让回溯更明显，我们一直都是引用记录数字的vector，因此我们需要回溯的时候直接pop_back()记录数组的vector即可

下面看代码

// 递归 + 回溯如何实现前序遍历？
// 每次往下遍历的时候都加入当前元素就OK
// 因为我们要加入的是全部路径，所以末尾的空元素我们是不需要的，所以递归的结束条件就是“左右孩子都为空”
class Solution {
public:
    void search(TreeNode *root,vector<int>& num,vector<string> &res) // 如果不对num加上引用，那么就只输出一次头结点
    {
        num.push_back(root->val);

        if(root -> left == NULL && root -> right == NULL)
        {
            string path;
            for(int i=0;i<num.size()-1;i++)
            {
                path += to_string(num[i]);
                path += "->";
            } // 因为最后一个节点的最后是没有“->”的，所以单独取出
            path += to_string(num[num.size()-1]);
            res.push_back(path); 
            return;
            // 这里没有return，太危险了！！！！！
        }

        // 然后向左遍历,注意要回溯
        if(root -> left!=NULL)  
        {
            search(root->left ,num,res);
            num.pop_back(); // vector中用pop_back去回溯
        }
        // 然后向右遍历
        if(root -> right!=NULL)
        {
            search(root->right ,num,res);
            num.pop_back();
        }
    }
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> res;
        vector<int> number;
        if(root == NULL) return res;
        search(root,number,res); // 没有返回值，直接全都加入到res数组中
        return res; 
    }
};