前言

一、问题描述

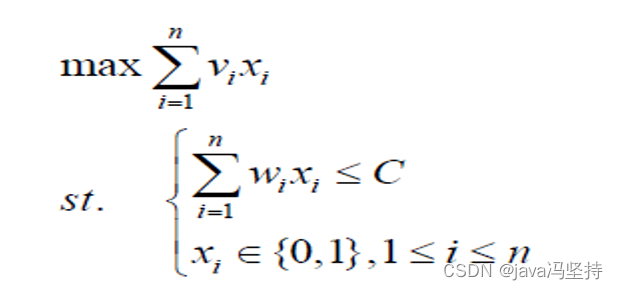
在这里插入图片描述

二、DP解决步骤

1、最优子结构性质

在这里插入图片描述

2、状态表示和递推方程

子问题可由两个参数确定：待考虑装包的物品集 和 背包的容量
将所有物品按照1至n 标号，待考虑装包的物品集可以用物品集中末尾物品的标号来描述，则得状态表示𝑽𝒂𝒍(𝒊,𝒑),1≤𝑖≤𝑛, 0≤𝑝≤𝐶 表示在背包容量为𝑝，待考虑装包的物品集为{1, 2, …, i}时的最大装入物品价值。
Val(n, C) 则表示原问题的最优解。

3、算法设计与分析

𝑽𝒂𝒍(𝒊,𝒑),1≤𝑖≤𝑛, 0≤𝑝≤𝐶 表示在背包总容量为𝑝，待考虑装包的物品集为{1, 2, …, i} 时的最大装入物品价值。
在这里插入图片描述

解释上图：

当 i = 1时：
- 如果w₁ > p，说明放不下背包，则价值为 0；
- 如果w₁ < p，则能放进去，且价值为 v₁。
当 i > 1时：
- 如果w_i > p 时，说明，整个包都放不下一个第i个物品，则这个物品可以舍弃，且价值为之前的i-1的价值即：Val(i - 1，p)
- 如果w_i < p时，说明，这个包是可以放得进去背包的，则需要判断值不值的：
  整个包能放下第i个物品，只有两种可能性：
  1. 不放第i个物品：价值仍然是val(i-1,p)
  2. 放入第i个物品：包中需要为其腾出 w_i 的空；那么前i-1个物品就只能从p-w_i 的空中选取最佳组合，其最佳组合值为 val(i-1,p-w_i) ；然后再加上v_i；
  然后，对这两种可能的子问题的最优值进行max；
  注意：前i-1个物品在不同的包容量Px下，其组合都是不同的，但是最佳值都可以用val(i-1,Px)来表示。在自底向上方法下，Px可以逐步累加，来求解val(i-1,Px)的值。

4、计算最优值

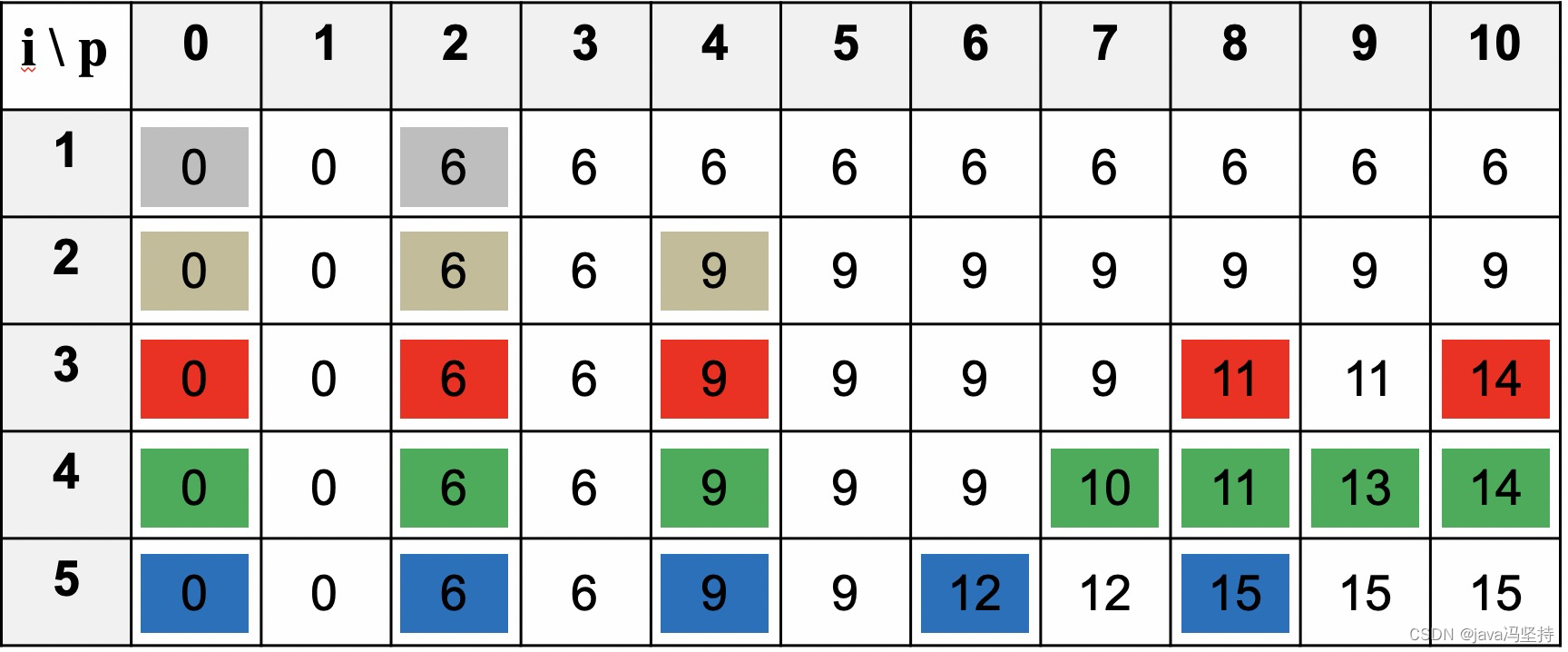
在这里插入图片描述

按物品的两种基本单位来给出表格的行数和列数，而不是根据物品的数目和价值！有枚举的意思，回顾暴力算法章节中剪绳子的问题！
3-6处的9：能放进去，但价值会降低，不腾，不放
3-8处的11：能放进去，但要腾1个，价值会升高，腾，放
3-10处的14：能放进去，但剩余空间够，不必腾，放，价值会升高

在这里插入图片描述

按照上面公式以及逻辑计算：

i = 1时，有11个情况，0-10，
物品只有第一个，n=1；
只有 p = 2及以后， p>=(w₁ = 2)，v₁ = 6，所以背包从 2 开始到 10 都是 6
（这里是第一个公式，往后就只使用第二个公式进行比较）
i = 2时，11个情况，0-10
物品是前2个，n=2；
p = 2时，满足p >= (w₂ = 2)，可以替换，但需要比较是否值得替换：Val(i-1, p)=Val(1,2)=6，Val(i-1, p - w₂)+v₂= Val(1,0)+3 = 3，3<；虽然能替换，放了还不如原来的价值，所以不替换。背包放 1 号物品；
p = 3时，同上。
p = 4时及以后（从逻辑上讲：背包放1号和2号物品，即9 正好，但是也需要计算）。p > (w₂ = 2)，可以放，但需要比较是否值得放：Val(i-1, p)=Val(1,4)=6，Val(i-1, p - w₂)+v₂= Val(1,2)+3 = 9，9>6，则可以放。
i = 3时，11个情况，0-10
物品有3个，n=3；
p = 2时，同上面的 p = 2 的逻辑。放物品1
p = 4时，同上面的 p = 4 的逻辑。放物品1，2
p = 8时，p >= (w₃ = 6)，可以替换，但需要比较是否值得替换：Val(i-1, p)=Val(2,8)=9，Val(i-1, p - w₃)+v₃= Val(2,2)+5 = 11，11>9，所以可以替换。把n=2拿出来，把n=3放进去，权重相加等于8，价值为11；放物品1,3
p = 10时，p >= (w₃ = 6)，可以替换，但需要比较是否值得替换 ：Val(i-1, p)=Val(2,10)=9，Val(i-1, p - w₃)+v₃= Val(2,4)+5 = 14。三个都可以放进去，则价值为14。放物品1，2，3
i = 4时，11个情况，0-10
物品有4个，n=4；
p = 2时，同上面的 p = 2 的逻辑。放物品1
p = 4时，同上面的 p = 4 的逻辑。放物品1，2
P = 7时，p >= (w₄ = 5)，可以替换，但需要比较是否值得替换 ，Val(i-1, p)=Val(3,7)=9，Val(i-1, p - w₄)+v₄= Val(3,2)+4 = 10，因为 9 < 10，所以可以放。放物品1，4
P = 8时，p >= (w₄ = 5)，可以替换，但需要比较是否值得替换 ，Val(i-1, p)=Val(3,8)=11，Val(i-1, p - w₄)+v₄= Val(3,3)+4 = 10，因为 11 > 10，所以替换，放物品1，3
P = 9时，p >= (w₄ = 5)，可以替换，但需要比较是否值得替换 ，Val(i-1, p)=Val(3,9)=11，Val(i-1, p - w₄)+v₄= Val(3,4)+4 = 13，因为 11 < 13 ，所以替换，放物品1，2，4
P = 10时，p >= (w₄ = 5)，可以替换，但需要比较是否值得替换 ，Val(i-1, p)=Val(3,10)=14，Val(i-1, p - w₄)+v₄= Val(3,5)+5 = 14，因为 14 = 14 ，所以替换，存物品1，2，3
i = 5时，11个情况，0-10
物品有5个，n=5；
略

5、算法实现

import java.util.Arrays;

import static java.lang.Math.max;

/**
 * DP之0-1背包问题
 */
public class Main3 {

    public static int MaxN = 11;
    public static int MaxC = 11;

    public static void main(String[] args) {
        int[] w = {2, 2, 6, 5, 4};
        double[] v = {6, 3, 5, 4, 6};
        double v1 = binaryKnapsack(w.length, w, v, 10);
        System.out.println(v1);
    }

    public static double binaryKnapsack(int numItems, int[] w, double[] v, int capacity) {
        double[][] val = new double[numItems][capacity + 1];
        memSet(val, 0, val.length);

        for (int i = 1; i < numItems; i++)
            for (int j = 0; j <= capacity; j++) {
                val[i][j] = val[i - 1][j];
                if (j >= w[i])
                    val[i][j] = max(val[i - 1][j], val[i][j - w[i]] + v[i]);
            }

        // 打印二维数组
        for (int i = 0; i < val.length; i++) {
            System.out.println(Arrays.toString(val[i]));
        }
        return val[numItems - 1][capacity]; // [4][10]
    }

    public static void memSet(double[][] val, int col, int length) {
        for (int i = 0; i < length; i++) {
            for (int j = 0; j < val[i].length; j++){
                val[i][j]=0;
            }
        }
    }

}