文章目录
- 1. 并查集
- 2. 哈夫曼编码树
1. 并查集
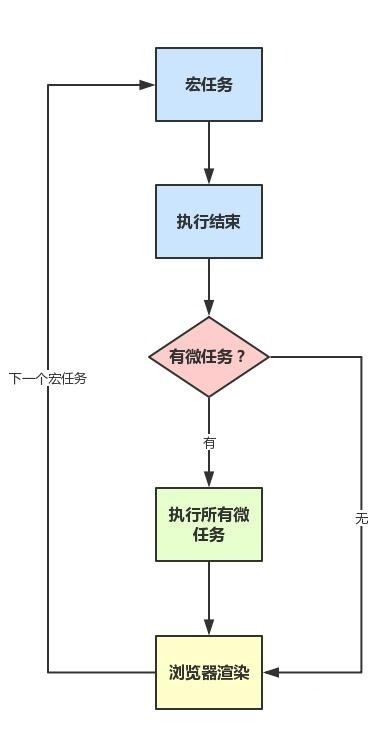
并查集是一个多棵树的集合(森林)。
并查集由多个集合构成,每一个集合就是一颗树。
并:合并多个集合。查:判断两个值是否再一个集合中。
每棵树存在数组中,使用双亲表示法。数组每个元素的父节点。如果没有父节点数组保存-1。根节点位置的数组值就算这颗树节点的个数。
eg:
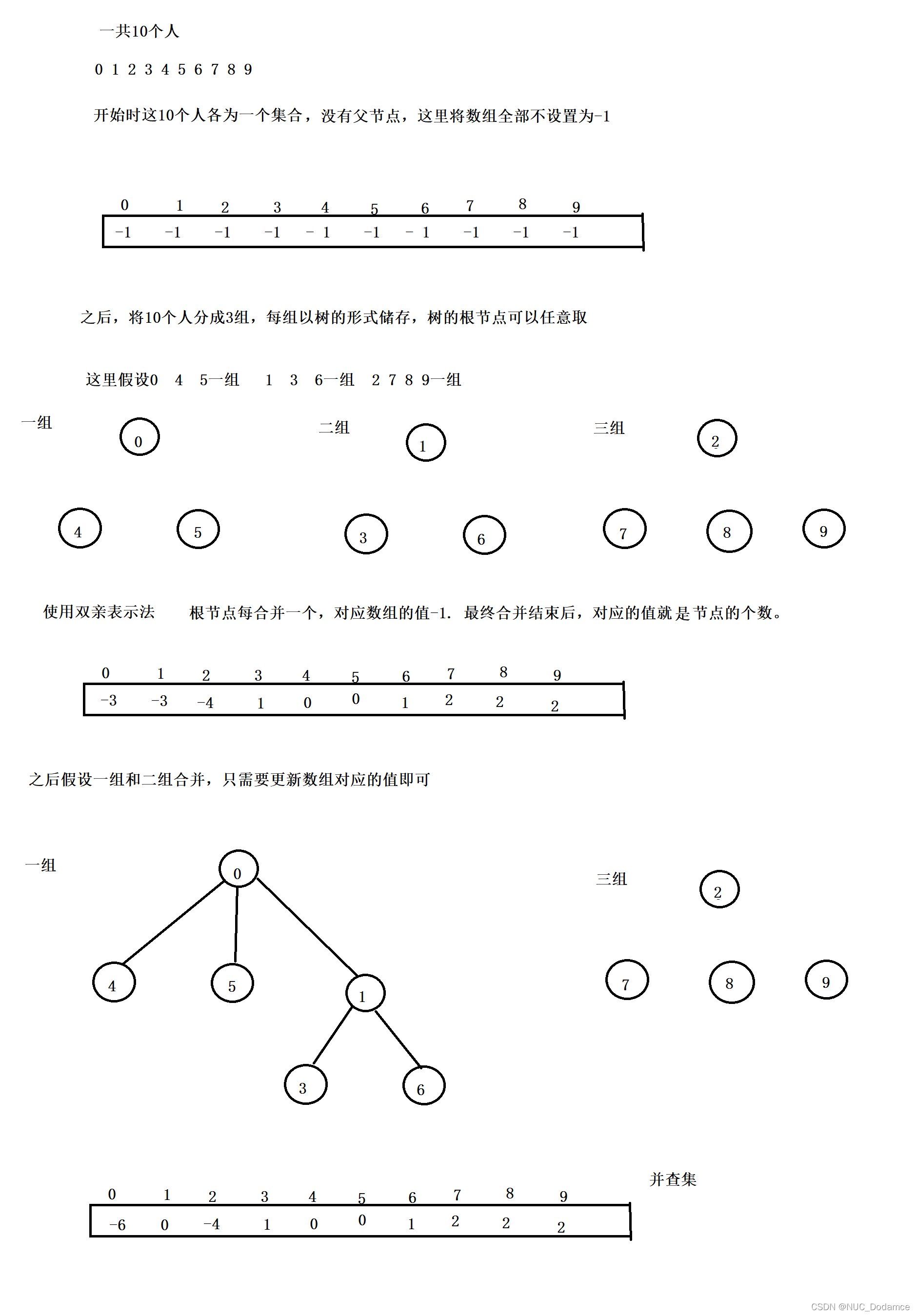
根据上图分析可知:
如果要合并的节点x和y不在一个树上
ufs[root_x] += ufs[root_y];(将y这个节点对应的子树和x的节点进行合并)
ufs[root_y] = root_x;(改变y这个节点的父亲节点)
根据上文可知,并查集查找的速度与树的高度有关。
当查找节点后,如果能将这个节点到根节点路径上的节点都直接插入到根节点上,则可以显著降低树的高度,从而提高效率。
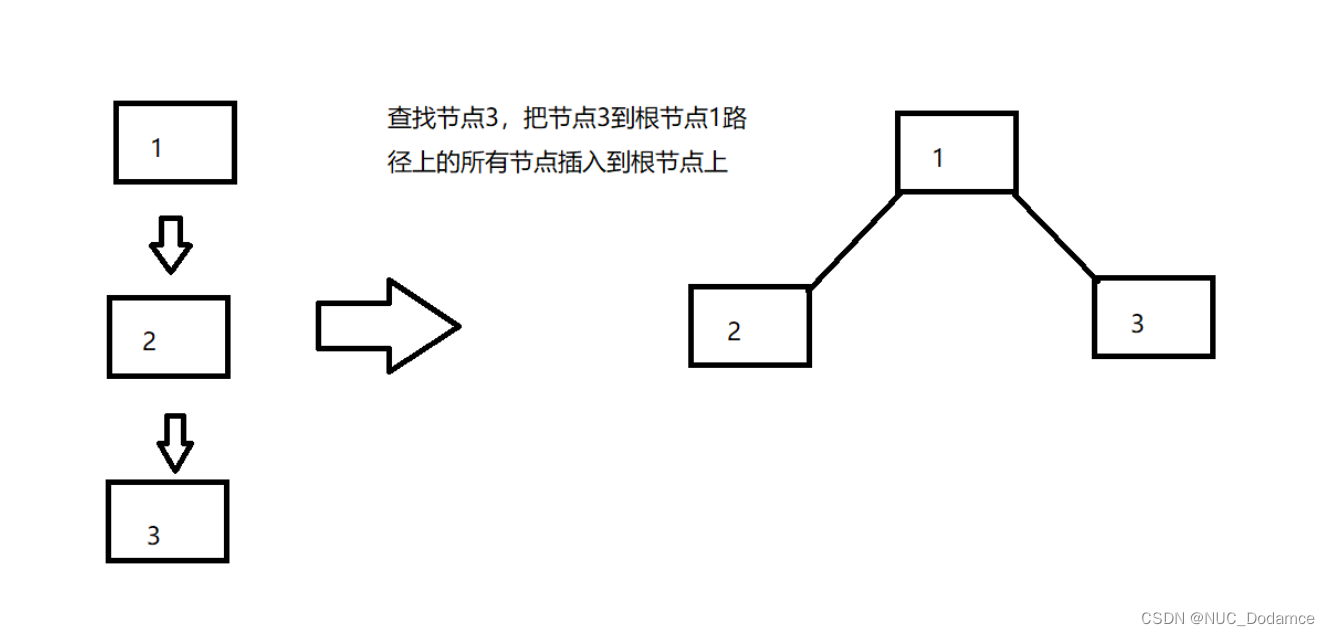
上述过程在查找节点的根节点时实现,找到根节点时先不返回,再遍历一遍更新节点的父节点即可。
把这个节点到根节点路径上的所有节点直接插入到根节点上
while (data != root)
{
int parent = ufs[data];
ufs[data] = root;
data = parent;
}
C++代码:
//构建并查集
#include <assert.h>
#include <vector>
#include <stdio.h>
class UnionFindSet
{
private:
//数组的下标保存的是并查集的数据,数组的值记录的是并查集这个节点的父节点下标
std::vector<int> ufs;
public:
UnionFindSet(size_t size)
{
ufs.resize(size, -1);
}
// x和y所在的两个集合合并
void Union(int x, int y)
{
assert(x < ufs.size() && y < ufs.size());
int root_x = FindRoot(x);
int root_y = FindRoot(y);
if (root_x != root_y)
{
//不在一棵树上
ufs[root_x] += ufs[root_y];
ufs[root_y] = root_x;
}
}
//找data的根
int FindRoot(int data)
{
int root = data;
while (ufs[root] >= 0)
{
root = ufs[root];
}
//找到根后,这里做优化,降低并查集树的高度
//把这个节点到根节点路径上的所有节点插入到根节点上
while (data != root)
{
int parent = ufs[data];
ufs[data] = root;
data = parent;
}
return root;
}
//获取并查集中树的个数
int GetTreeSize()
{
int ret = 0;
for (int i = 0; i < ufs.size(); i++)
{
if (ufs[i] < 0)
ret += 1;
}
return ret;
}
//打印并查集信息
void PrintUfs()
{
for (int i = 0; i < ufs.size(); i++)
{
printf("%2d ", i);
}
printf("\n");
for (int i = 0; i < ufs.size(); i++)
{
printf("%2d ", ufs[i]);
}
printf("\n");
}
};
#include "UnionFindSet.h"
#include <iostream>
int main(int argc, char const *argv[])
{
UnionFindSet set(9);
for (int times = 0; times < 8; times++)
{
//打印并查集树的个数
std::cout << set.GetTreeSize() << std::endl;
set.PrintUfs();
set.Union(times, times + 1);
}
std::cout << set.GetTreeSize() << std::endl;
set.PrintUfs();
return 0;
}

2. 哈夫曼编码树
哈夫曼树:
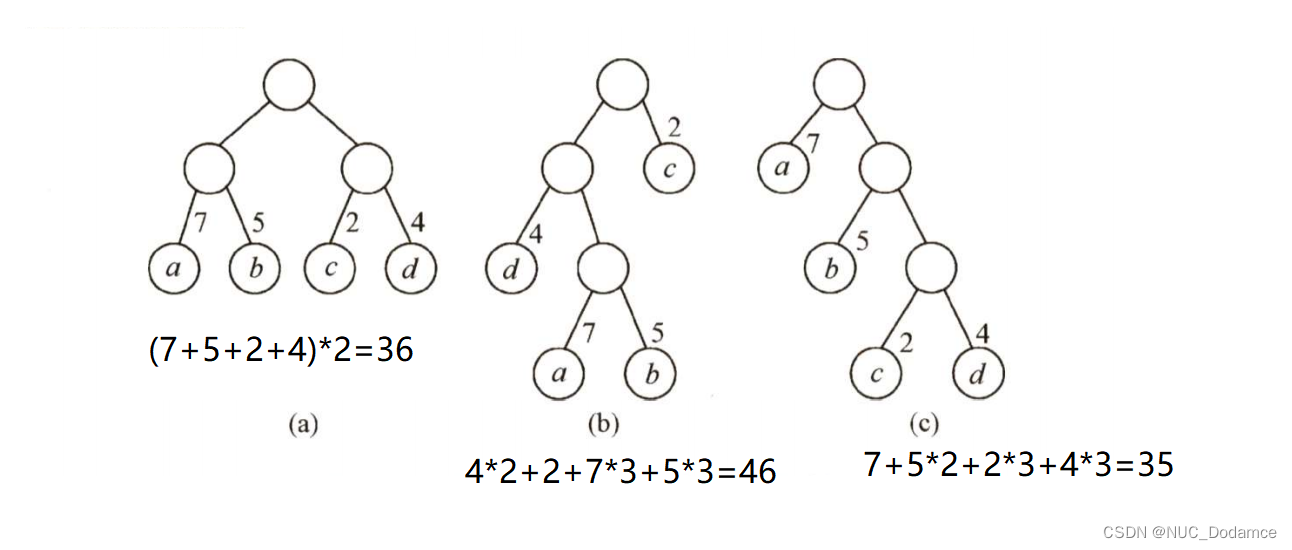
在许多应用中,树中结点常常被赋予一个表示某种意义的数值,称为该结点的权。
从树的根到任意结点的路径长度(经过的边数)与该结点上权值的乘积,称为该结点的带权路径长度。
树中所有叶结点的带权路径长度之和称为该树的带权路径长度。
哈夫曼编码:
哈夫曼编码就是在哈夫曼树的基础上构建的,这种编码方式最大的优点就是用最少的字符包含最多的信息内容,进而实现信息的压缩存储。
根据发送信息的内容,通过统计文本中相同字符的个数作为每个字符的权值,建立哈夫曼树。对于树中的每一个子树,统一规定其左孩子标记为 0 ,右孩子标记为 1 。这样,用到哪个字符时,从哈夫曼树的根结点开始,依次写出经过结点的标记,最终得到的就是该结点的哈夫曼编码。
文本中字符出现的次数越多,在哈夫曼树中的体现就是越接近树根。编码的长度越短。
eg:
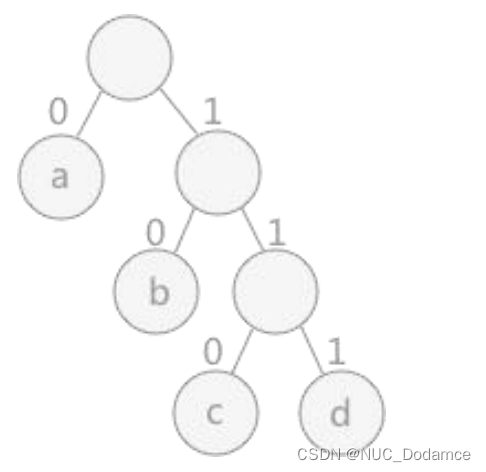
这是用权值分别为 7、5、2、4 的字符 a、b、c、d 构建的哈夫曼树。
显然,字符 a 用到的次数最多,所以它对应的哈弗曼编码应最短,这里用 0 表示;其次,是字符 b 用的多,因此字符 b 编码为 10 ,
以此类推,字符 c 的编码为 110 ,字符 d 的编码为 111。
权值越大,表示此字符在文件中出现的次数越多,那么,为了实现用最少的字符包含最多的内容,就应该给出现次数越多的字符,分配的哈弗曼编码越短。
使用程序求哈夫曼编码有两种方法:
- 从叶子结点一直找到根结点,逆向记录途中经过的标记。例如,上图中字符 c 的哈夫曼编码从结点 c 开始一直找到根结点,结果为:0 1 1 ,所以字符 c 的哈夫曼编码为:1 1 0(逆序输出)。
- 从根结点出发,一直到叶子结点,记录途中经过的标记。例如,上图中字符 c 的哈夫曼编码,就从根结点开始,依次为:1 1 0。
需要注意:
注意:0和1究竟是表示左子树还是右子树没有明确规定。
左、右孩子结点的顺序是任意的, 所以构造出的哈夫曼树并不唯一,但各哈夫曼树的带权路径长度WPL相同且为最优。
此外,如有若干权值相同的结点,则构造出的哈夫曼树更可能不同,但WPL必然相同且是最优的
哈夫曼树构造流程:
给定N个权值分别为W1, W2,…,Wn”的结点,构造哈夫曼树的算法描述如下:
- 将这n个结点分别作为n棵仅含一个结点的二叉树,构成森林F。
- 构造一个新结点,从F中选取两棵根结点权值最小的树作为新结点的左、右子树,并且将新结点的权值置为左、右子树上根结点的权值之和。
- 从F中删除刚才选出的两棵树,同时将新得到的树加入F中。
- 重复步骤2和3,直至F中只剩下一棵树为止。
从上述构造过程中可以看岀哈夫曼树具有如下特点:
- 每个初始结点最终都成为叶结点,且权值越小的结点到根结点的路径长度越大。
- 构造过程中共新建了n-1个结点(双分支结点),因此哈夫曼树的结点总数为2*n-1
- 每次构造都选择2棵树作为新结点的孩子,因此哈夫曼树中不存在度为1的结点。
C++代码:
#include <iostream>
#include <unordered_map>
#include <string>
#include <vector>
#include <assert.h>
//传入一串字符,使用哈夫曼树对其进行编码,字符串中每个字符出现的次数就是作为哈夫曼树的权值
struct TreeNode
{
char val; //节点保存的值
int weight; //权值
TreeNode *left;
TreeNode *right;
TreeNode(int _weight) : val(0), weight(_weight), left(nullptr), right(nullptr) {}
TreeNode(char _val, int _weight) : val(_val), weight(_weight), left(nullptr), right(nullptr) {}
};
class HuffTree
{
private:
void _InitTimes(const std::string &src)
{
for (int i = 0; i < src.size(); i++)
{
times[src[i]] += 1;
}
}
void _PreDisplay(TreeNode *node, std::string &str)
{
if (node->left == nullptr && node->right == nullptr)
{
//叶子节点
// std::cout << str << std::endl;
code[node->val] = str;
return;
}
if (node->left != nullptr)
{
str.push_back('0');
_PreDisplay(node->left, str);
str.pop_back(); //出递归后,刚刚递归进去给字符串插入的字符也要弹出
}
if (node->right != nullptr)
{
str.push_back('1');
_PreDisplay(node->right, str);
str.pop_back();
}
}
void _PreDisplay(TreeNode *node)
{
std::string retBuff;
_PreDisplay(node, retBuff);
}
public:
TreeNode *root; //构造的哈夫曼树
std::unordered_map<char, std::string> code; //保存字符进行编码的结果
std::unordered_map<char, int> times; //保存传入的字符串中每个字符出现的次数
HuffTree(const std::string &src)
{
//统计每个字符出现的次数
_InitTimes(src);
std::vector<TreeNode *> ArrayNode;
//先给所有节点开辟空间
std::unordered_map<char, int>::iterator pos = times.begin();
while (pos != times.end())
{
ArrayNode.push_back(new TreeNode(pos->first, pos->second));
pos++;
}
//循环创建哈夫曼树节点
//如果只有一个节点
if (ArrayNode.size() == 0)
{
root = ArrayNode[0];
}
else
{
for (int time = 0; time < ArrayNode.size() - 1; time++)
{
//找权值最小的和第二小的节点
int minIndex = 0;
int minSecIndex = 0;
// ArrayNode[minIndex] == nullptr证明这个节点已经建立过哈夫曼树了,需要跳过
while (ArrayNode[minIndex] == nullptr)
{
minIndex++;
}
for (int i = 0; i < ArrayNode.size(); i++)
{
if (ArrayNode[i] != nullptr && ArrayNode[i]->weight < ArrayNode[minIndex]->weight)
{
minIndex = i;
}
}
//找次小值
while (ArrayNode[minSecIndex] == nullptr || minIndex == minSecIndex)
{
minSecIndex++;
}
for (int i = 0; i < ArrayNode.size(); i++)
{
if (i != minIndex)
{
if (ArrayNode[i] != nullptr && ArrayNode[i]->weight < ArrayNode[minSecIndex]->weight)
{
minSecIndex = i;
}
}
}
// printf("出现次数最小的字符是%c,出现次数%d\n", ArrayNode[minIndex]->val, ArrayNode[minIndex]->weight);
// printf("出现次数次少的字符是%c,出现次数为%d\n", ArrayNode[minSecIndex]->val, ArrayNode[minSecIndex]->weight);
// printf("============\n");
//创建新节点,将这个节点插入到最小字符位置,次少节点位置处理过了置空.并将树结构构造好
root = new TreeNode(ArrayNode[minIndex]->weight + ArrayNode[minSecIndex]->weight);
root->left = ArrayNode[minIndex];
root->right = ArrayNode[minSecIndex];
ArrayNode[minIndex] = root;
ArrayNode[minSecIndex] = nullptr;
}
}
}
//打印编码
void PrintCode()
{
//遍历树,直到遍历到叶子节点,规定向左树走编码为0,向右树走编码为1
_PreDisplay(root);
//打印编码集合
auto pos = code.begin();
while (pos != code.end())
{
std::cout << pos->first << ":" << pos->second << std::endl;
pos++;
}
}
//解码
char DeCode(const std::string &src)
{
TreeNode *node = root;
for (int i = 0; i < src.size(); i++)
{
if (src[i] == '0')
node = node->left;
if (src[i] == '1')
node = node->right;
}
assert(node->left == nullptr && node->right == nullptr); // node一定走到了叶子节点
return node->val;
}
};
#include "hufftree.h"
int main(int argc, char const *argv[])
{
HuffTree tree("abandon");
tree.PrintCode();
std::cout << "010解码:" << tree.DeCode("010") << std::endl;
return 0;
}
这里构建的哈夫曼树如下图:
abandon中
a出现2次,b出现1次,n出现2次,d出现1次,o出现1次。次数作为整个节点的权值


需要注意的是,这里对其编码使用一个字符‘1’或‘0’进行编码,压缩效果不明显。
正式做项目时,可以选择树向左移动时,代表比特位0,向右移动时代表比特1。这样才可以真正达到压缩效果。
具体细节可以移步数据结构-压缩软件核心-C++(利用哈夫曼树进行编码,对文件进行压缩与解压缩)
代码位置Github