本博客参考：《python数学实验与建模 》

时间序列

时间序列数据是按照时间顺序排列的、随着时间变化且相互关联的数据序列，这类数据往往反映了某一事物、现象等随时间的变化状态或程度。
常用的时间序列预测方法有多种：移动平均法、加权序时平均数法、移动平均法、加权移动平均法、趋势预测法、指数平滑法、季节性趋势预测法、市场寿命周期预测法等等，本篇博客浅谈指数平滑法

指数平滑

指数平滑法实际上是一种特殊的加权移动平均法，与一次移动平均法相比，后者认为最近N期数据对于未来的值影响相同，即都加权$\frac{1}{N}$；并且N以前的数据对未来值没有影响，加权为0，即某一期的预测值为
$$y_t^p=\frac{1}{N}(y_{t-1}+....+y_{t-N})$$

二次移动平均法及更高次移动平均法的权数不是$\frac{1}{N}$，并且次数越高,权数的结构越复杂，但是永远保持对称的权数，即两端项权数小、中间项权数大，这种方法的缺点是预测值总是停留在过去的水平上而无法预计会导致将来更高或更低的波动，不符合一般系统的动态性
一般，历史数据对于未来值的影响是随时间间隔的增长而是递减的，下面我们对指数平滑法的原理进行简要说明

一次指数平滑

设原始时间序列为
$$y=[y_1,y_2,...,y_t]$$
设加权系数$\alpha$，$0<\alpha <1$

假设我们想要知道$y_{t+1}$的值，那么经过一次指数平滑预测，我们可以得到

$$\begin{array}{rlrl}{y}_{t+1}^p=& S_t^{(1)}& & \\ =& \alpha y_t+(1-\alpha )S_{t-1}^{(1)}& & \\ =& S_{t-1}^{(1)}+\alpha (y_t-S_{t-1}^{(1)})& & \\ =& y_t^p+\alpha (y_t-y_t^p)& & (y_t^p表示y_t的预测值)\end{array}\text{\hspace{1em}(1)}$$

1. $S_t^{(1)}$表示第t次的一次指数平滑值，将其展开
   $$\begin{array}{rl}{S}_t^{(1)}=& \alpha y_t+(1-\alpha )S_{t-1}^{(1)}\\ =& \alpha y_t+(1-\alpha )[\alpha y_{t-1}+(1-\alpha )S_{t-2}^{(1)}]\\ =& ..\\ =& \alpha \sum _{i=0}^{\infty }(1-\alpha {)}^i{y}_{t-i}\end{array}$$
   从上面的式子中我们会发现$S_t^{(1)}$的实质是全部原始数据的加权平均值
2. 加权系数$\alpha$规定了新数据和原数据所占比重的大小
   从式子（2）中我们可以看出，新的预测值是根据预测误差对原预测值进行修正得到的，加权系数的大小代表着修正幅度的大小，下面我们来看两种极端情况

$\alpha =0$表示下期预测值等于本期预测值，即不考虑任何新的信息
$\alpha =1$表示下期预测值等于本期预测值，即完全不相信过去的信息

上述情况对现实中的数据预测意义不大，因此我们要选择合适的加权系数使得$0<\alpha <1$，选取原则如下：
(1)时间序列波动不大且比较平稳，$\alpha$值应小一些，这样可以使得模型能够包含较长时间序列的信息
（2）时间序列具有迅速且明显的变动倾向，$\alpha$值应大一些，使得模型的预测值能够迅速跟上数据的变化
3. 关于初始指数平滑值$S_0^{(1)}$
(1)当时间序列的数据较多(n>20)，$S_0^{(1)}$对于后面的预测值影响很小，可取时间序列的初始值作为$S_0^{(1)}$，即$S_0^{(1)}=y_0$
(2)当时间序列的数据较少(n<20)，$S_0^{(1)}$对于后面的预测值影响较大，可以取最初m个时间序列数据的平均值作为$S_0^{(1)}$，即$S_0^{(1)}=\frac{y_0+y_1+...+y_m}{m}$

预测示例

已知美国1790-2000年每隔10年的人口数据，请对2010年的美国人口进行预测

年份	1790	1800	1810	1820	1830	1840	1850	1860	1870	1880	1890	1900	1910	1920	1930	1940	1950	1960	1970	1980	1990	2000
人口	3.9	5.3	7.2	9.6	12.9	17.1	23.2	31.4	38.6	50.2	62.9	76.0	92.0	106.5	123.2	131.7	150.7	179.3	104.0	226.5	251.4	281.4

（1）加权系数$\alpha$的确定
仅仅从初始数据，我们并不能看出数据特征，因此我们尝试选取不同的加权系数并查看各自的预测效果，我们将分别取$\alpha =0.2、0.5、0.8$

（2）取初始指数平滑值$S_0^{(1)}=y_0=5.3$
（3）根据预测模型：$y_{t+1}^p=y_t^p+\alpha (y_t-y_t^p)$进行预测

代码

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
y=np.array([3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,
           38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,
           150.7,179.3,204.0,226.5,251.4,281.4])
y.shape
>>> (22,)       
# 定义一次指数平滑函数
def expmove(y,alpha):
    n=len(y)
    M=np.zeros(n)# 生成空序列，用于存储指数平滑值M
    M[0]=y[0]# 初始指数平滑值的赋值
    for i in range(1,len(y)):
        M[i]=alpha*y[i-1]+(1-alpha)*M[i-1]# 开始预测
    return M   
# 使用三种alpha值查看预测效果
y_pred1=expmove(y,0.2)
y_pred2=expmove(y,0.5)
y_pred3=expmove(y,0.8)# 注意，此处的y_pred是一个预测序列，并非一个值
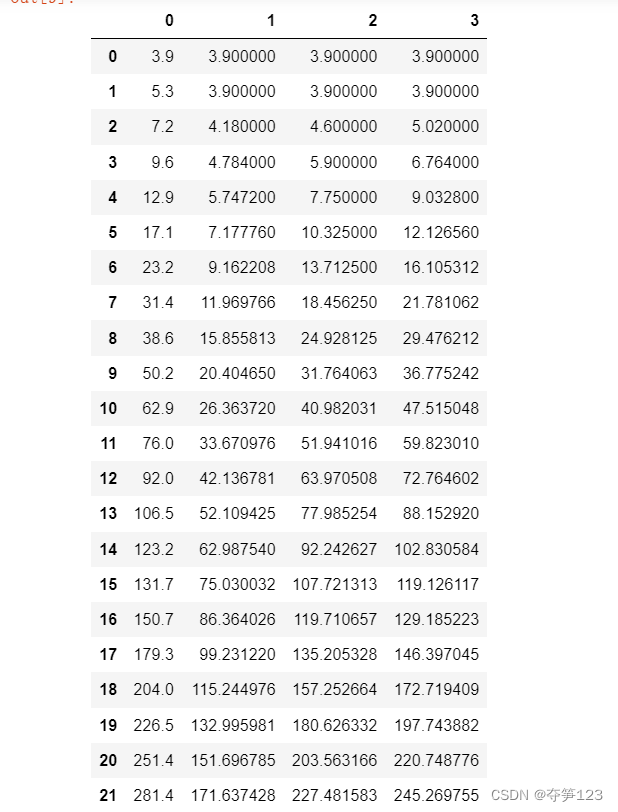
# 查看预测数据
d=pd.DataFrame(np.c_[y,y_pred1,y_pred2,y_pred3])
d

# 可视化查看预测值与真实值的对比
plt.figure(figsize=(12,8))
plt.plot(y,label='y')
plt.plot(y_pred1,label='y1')
plt.plot(y_pred2,label='y2')
plt.plot(y_pred3,label='y3')
plt.grid()
plt.legend()           

运行结果

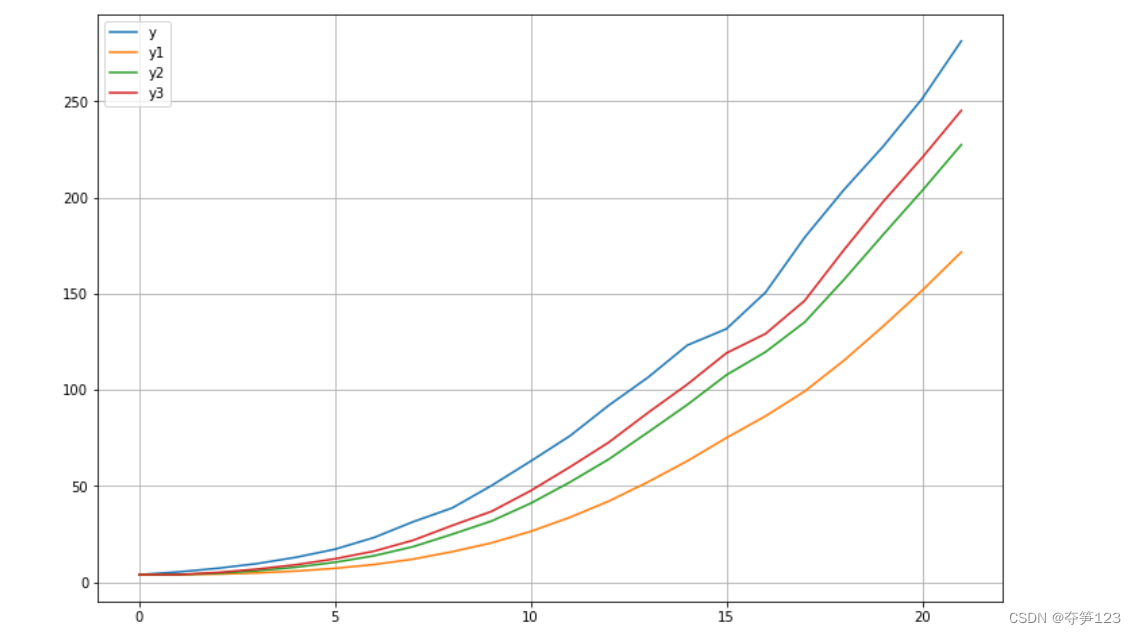
从上面的图像中我们看到$\alpha =0.8$的预测效果更好，我们使用$\alpha =0.8$预测时间序列的下一期数据

y_pred2010=0.8*y_pred3[-1]+(1-0.8)*y_pred3[-1]
y_pred2010
>>> 245.26975527147619

二次指数平滑

当时间序列的变动出现直线趋势时，一次指数平滑预测值存在明显的滞后偏差¹，因此需要将这种滞后误差加以修正，可以在一次指数平滑的基础上进行二次指数指数平滑

上面我们我们知道一次指数平滑值
$$S_t^{(1)}=S_{t-1}^{(1)}+\alpha (y_t-S_{t-1}^{(1)})\text{\hspace{1em}(1)}$$
那么二次指数平滑值
$$S_t^{(2)}=a{S}_t^{(1)}+(1-\alpha )S_{t-1}^{(2)}\text{\hspace{1em}(2)}$$
当时间序列$y_t$从某时期开始具有直线趋势，可用直线
$$y_{t+m}^p=a_t+b_{t}m（其中m表示待预测的第m期数据）\text{\hspace{1em}(3)}$$
进行趋势预测，截距和斜率的值如下²

$$\{\begin{array}{l}{a}_t=2S_t^{(1)}-S_t^{(2)}\\ b_t=\frac{\alpha }{1-\alpha }(S_t^{(1)}-S_t^{(2)})\end{array}$$

预测示例

已知某家具城近十年的销售额如下，请预测该家具城明、后两年的销售额

年份	2013	2014	2015	2016	217	2018	2019	2020	2021	2022
销售额	2828	2949	2995	3181	3220	3384	3497	3702	3813	3948

（1）加权系数$\alpha$的确定
根据上述数据我们可以看出数据的波动不大，基本呈线性趋势，因此我们可以将加权系数的值适当取小一些，取$\alpha =0.4$

（2）取初始指数平滑值$S_0^{(1)}=S_0^{(2)}=y_0=2828$
根据公式（1）（2）计算指数平滑值

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
alpha=0.4
# 定义指数平滑函数
def expmove(y,alpha=0.4):
    n=len(y)
    M=np.zeros(n)# 生成空序列，用于存储指数平滑值M
    M[0]=y[0]# 初始指数平滑值的赋值
    for i in range(1,len(y)):
        M[i]=alpha*y[i-1]+(1-alpha)*M[i-1]# 开始预测
    return M  
# 一次指数平滑序列
ss1=expmove(y)
# 二次指数平滑序列
ss2=expmove(ss1)

（3）根据公式（3）对时间序列的值进行预测

# 预测原时间序列
y_pred=np.zeros(len(y))
for i in range(1,len(y)):
    y_pred[i]=2*ss1[i-1]-ss2[i-1]+alpha/(1-alpha)*(ss1[i-1]-ss2[i-1])
# 2023
y_pred2023=2*ss1[-1]-ss2[-1]+alpha/(1-alpha)*(ss1[-1]-ss2[-1])*1
# 2024
y_pred2024=2*ss1[-1]-ss2[-1]+alpha/(1-alpha)*(ss1[-1]-ss2[-1])*2
y_pred2023,y_pred2024
>>>(4128.513034240001, 4335.155486720001)
# 查看预测数据
d=pd.DataFrame(np.c_[y,ss1,ss2,y_pred])
d

运行结果

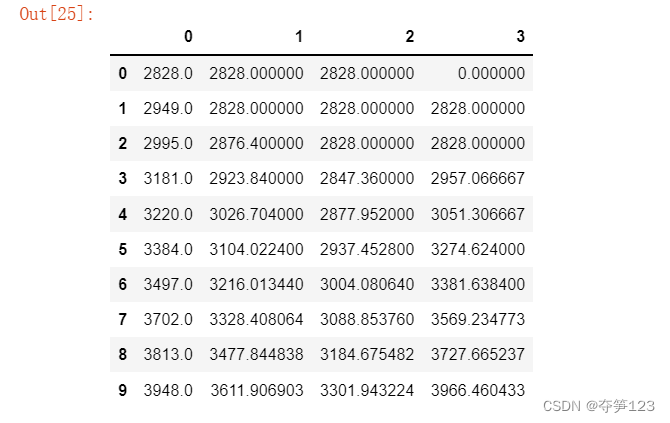
# 对预测数据进行简单的处理
y_pred=np.append(y_pred,[y_pred2023,y_pred2024])
y_pred[0]=y[0]
# 可视化查看预测值与真实值的对比
plt.figure(figsize=(12,8))
plt.plot(y,label='y')
plt.plot(ss1,label='ss1')
plt.plot(ss2,label='ss2')
plt.plot(y_pred,label='y_pred')
plt.grid()
plt.legend() 

运行结果

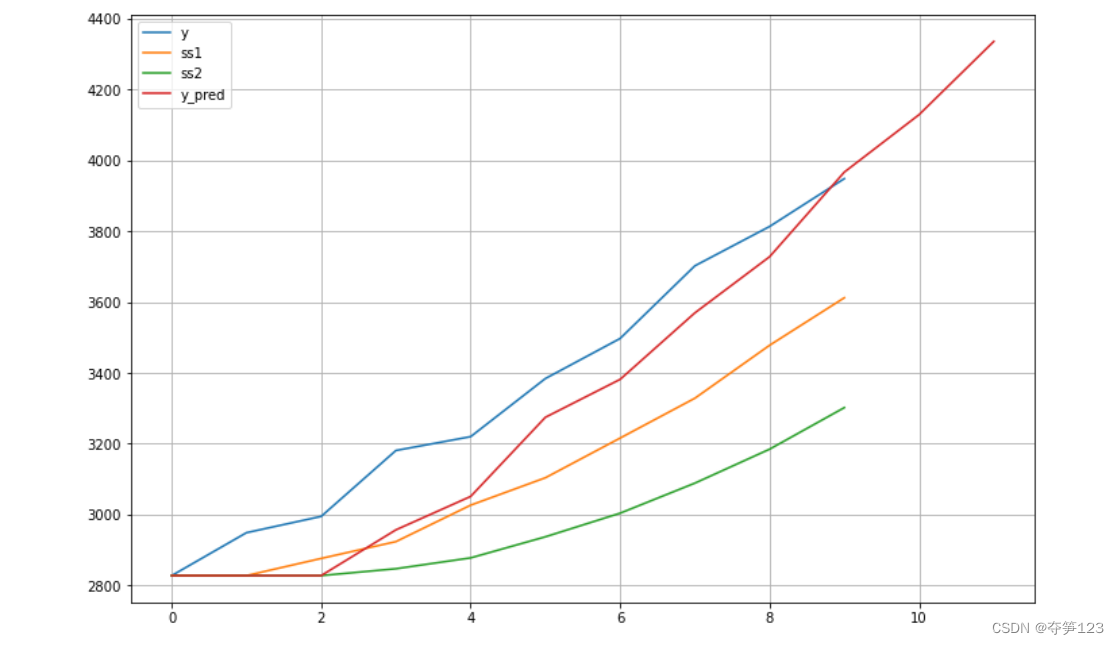
三次指数平滑

To be continued

---

1. 这里应该是需要推导一下的 ↩︎

2. 这里应该也需要推导一下 ↩︎