全文目录

• 🤔一维差分
• • 😕差分数组的构建
• 🤔二维差分
• • 😕差分矩阵的构建

---

🤔一维差分

首先来了解一下差分的性质，差分是前缀和的逆运算，如果说前缀和是：S = f(n) ，那么差分就是 D = f^-1(n) ，也就是说，原数组是差分数组的前缀和。

原数组：a[i]，差分数组：b[i]

差分数组满足：

a[0 ]= 0;

b[1] = a[1] - a[0];

b[2] = a[2] - a[1];

b[3] = a[3] - a[2];
...
b[i] = a[i] - a[i - 1];

原数组满足：

a[i] = b[1] + b[2] + ... + b[i];

差分数组一般用来将原数组中的一段区间加上或减去一个值。

---

差分数组的特性：

因为原数组是差分数组的前缀和，所以我们可以通过差分数组来求原数组。

那么，当差分数组中的某个位置 b[i] 发生了改变，通过差分数组求出来的原数组 a[i] 及之后的全部元素都会发生对应的变化。

但是如果只是对一段区间 [l, r] 的数据进行操作的话，上述操作会导致 r 后面的数据也发生了变化，所以需要对 b[r + 1] 进行反操作，来弥补这个问题。

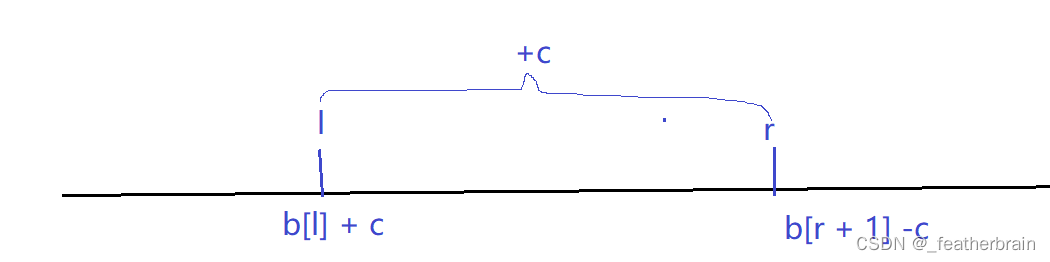
代码：

b[l] += c;
b[r + 1] -= c;

😕差分数组的构建

在构建差分数组的时候，可以将原数组看作全是 0 的数组，原数组中的每一个元素都是可以看作是新插入的元素，也就是对 [i, i] 这个区间进行了插入 a[i] 的操作。

---

🤔二维差分

原数组 a[][] ， 差分数组 b[][]

二维差分与一维差分的性质一样，只是作用范围有些不同，但是同样满足：

1. 原矩阵a[][] 是差分矩阵b[][] 的前缀和数组，

2. 通过差分矩阵来求原矩阵时，对差分矩阵中的某个元素 b[i][j] 进行 +- c，原矩阵中包括 a[i][j] 在内，右下角的全部元素都会 +- c

例：对差分数组进行 b[x1][y1] +- c，受影响的就是原数组中标绿的元素

二维差分的应用跟二维前缀和很相似，就是对原矩阵中的一个子矩阵插入一个值，如对以 x1, y2 为左上角， x2, y2 为右下角的矩阵插入一个值，就是对绿色部分的值插入一个值：

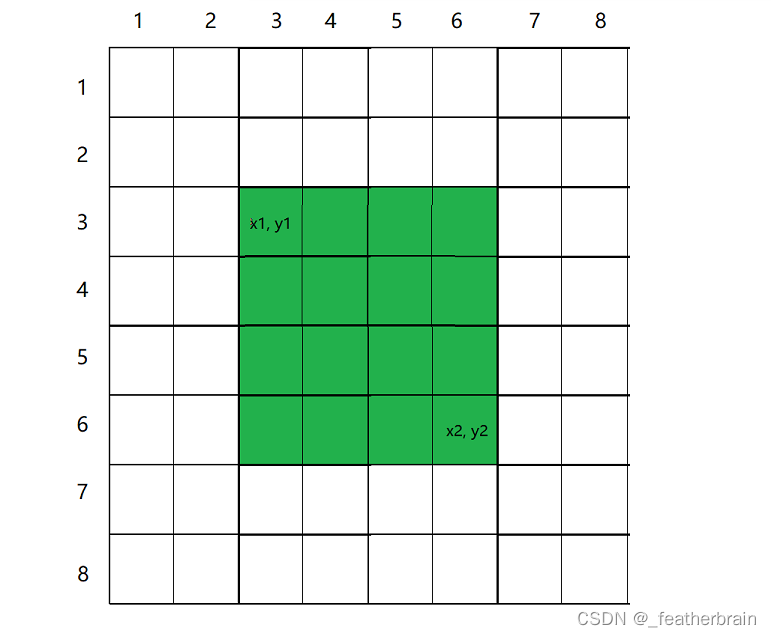
这个插入操作可以类比二维前缀和求和的操作，将多余的部分减去，再将多减去的部分加上，只不过，因为差分是前缀和的逆运算，所以前缀和是影响左上角，差分影响的是右下角。

插入代码：

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

根据二维差分的影响范围来说，可以利用画图来加深一下理解：

b[x1][y1] += c;

b[x1][y1] += c;
b[x1][y2 + 1] -= c;

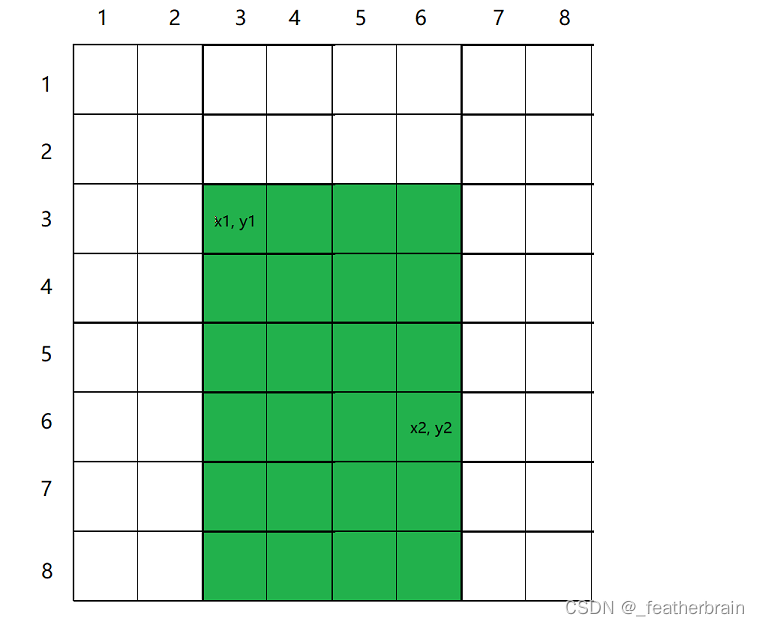
b[x1][y1] += c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y1] -= c;

// 红色表示多减去的部分，下一步需要加上

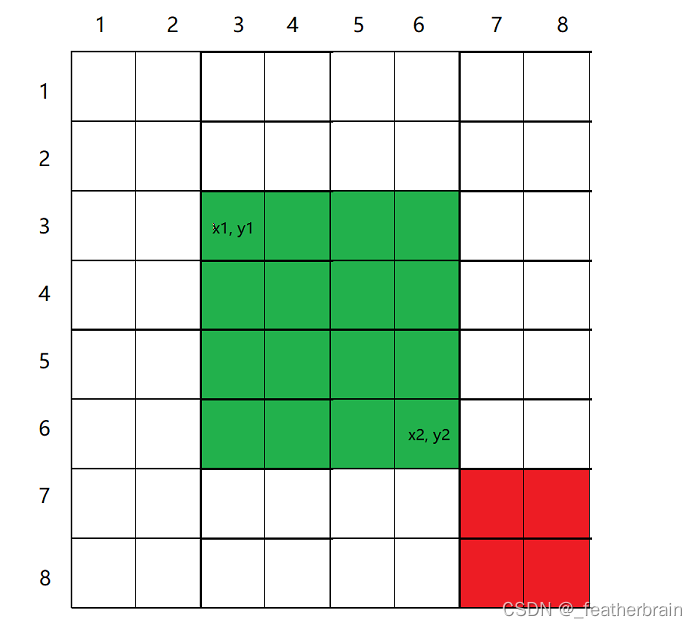
b[x1][y1] += c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y1] -= c;
b[x2 + 1][y2 + 1] += c;

这样，通过差分矩阵来求原数组的时指定的子矩阵就在 O(1) 的时间内得到了相应的操作。

😕差分矩阵的构建

我们可以想象原数组a[][]中全是0，那么对应的，它的差分矩阵b[][] 也是全是0。对于 a[][]中的每一个元素，我们就可以想象成是插入了以 c(c == a[i][j])，也就是对每个x1 == x2 == i, y1 == y2 == j的小矩阵进行了插入操作。

当 b[i][j]矩阵中全部插入了对应的 a[i][j]时，差分矩阵就构建完成了。

---

完结散花🌈🌈🌈