神经网络的损失函数

1.损失函数的引入

    在之前的学习中，我们建立神经网络时总是先设定好w与b的值,或者由我们调用的PyTorch类帮助我们随机生成权重向量,接着通过加和求出z ,再在z上嵌套sigmoid或者softmax函数，最终获得神经网络的输出。
 神经网络的计算是从左侧向右侧计算的.这是神经网络的正向传播过程。但这并不是神经网络算法的全流程，这个流程虽然可以输出预测结果，但却无法保证神经网络的输出结果与真实值接近。
  此时,我们就要训练神经网络,求解一组最适合的w和b,令神经网络的输出结果与真实值接近,这就是神经网络模型训练的目标.

2.损失函数

    比如我们做了一个预测房价的实验,预测的房价和真正的房价之间肯定存在差异.当真实值与预测值差异越大时，我们就认为神经网络学习过程中丢失了许多信息，丢失的这部分称为”损失“，因此评估真实值与预测值差异的函数被我们称为“损失函数.

损失函数   1.在数学上，表示为以需要求解的权重向量ω为自变量的函数L(ω)。   2.衡量真实值与预测结果的差异，评价模型学习过程中产生的损失的函数。   3.如果损失函数的值很小,则说明模型预测值与真实值很接近,模型训练得很好

    我们希望损失函数越小越好,以此,我们将问题转变为求解函数L(ω)的最小值所对应的自变量ω.

3.回归：误差平方和SSE

SSE误差平方和:

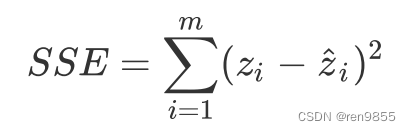
    其中z_i(公式的前者)是样本i的真实值,而z_ihat(公式的后者)是样本i的预测值。对于全部样本的平均损失,则可以写作:

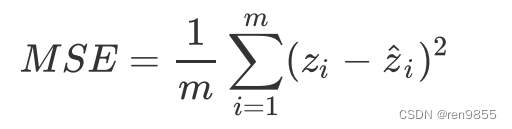
3.1 MSE的使用

# 按照MSE的公式,pytorch已经写好了函数,直接调用就行

import torch
from torch.nn import MSELoss 

yhat=torch.randn(size=(50,),dtype=torch.float32)
y=torch.randn(size=(50,),dtype=torch.float32)

criterion=MSELoss() 
loss = criterion(yhat,y)
loss

输出结果:

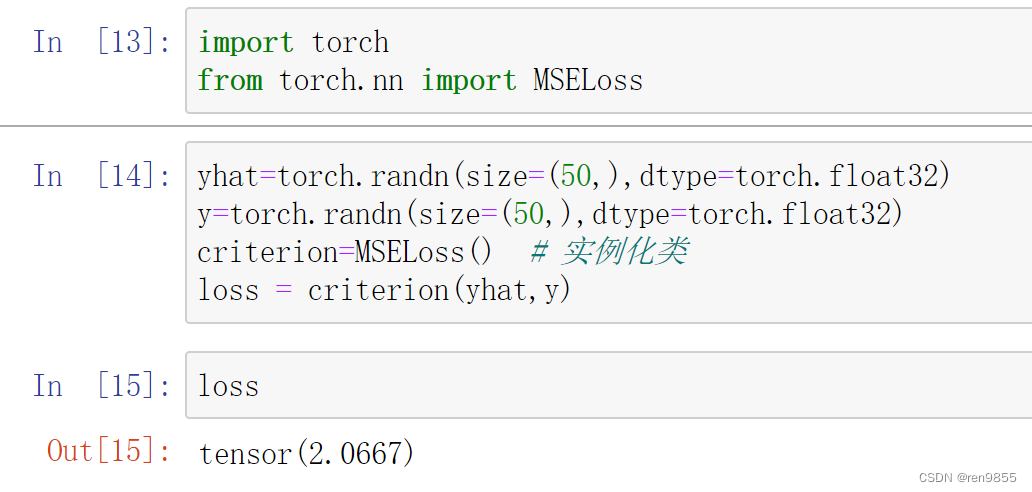
3.2 二分类交叉熵损失函数

    在这一节中，我们将介绍二分类神经网络的损失函数：二分类交叉熵损失函数,也叫做对数损失.
 大多数时候，除非特殊声明为二分类，否则提到交叉熵损失，我们会默认算法的分类目标是多分类.
 二分类交叉熵损失函数是由极大似然估计推导出来的，对于有m个样本的数据集而言，全部样本上的平均损失写作：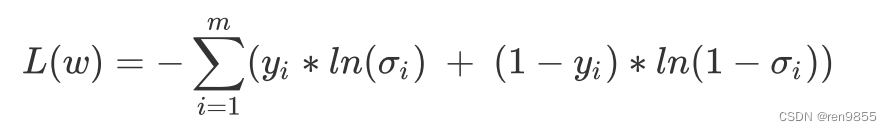
单个样本损失:

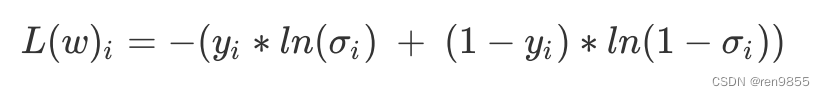
    在公式中,ln是以自然底数为底的对数函数,ω表示求解出来的一组权重(ω在σ里),m是样本的个数,y_i是样本i上真实的标签,σ_i是样本i上基于参数计算出来的sigmoid函数的返回值,x_i是样本i各个特征的取值。

3.3 极大似然估计推导二分类交叉熵损失

    极大似然估计,如果一个事件的发生概率很大，那这个事件应该很容易发生。
 寻找相应的权重ω,使得目标事件的发生概率最大,就是极大似然估计的基本方法。

---

    二分类神经网络的标签是[0,1],样本i在由特征向量x_i和权重向量ω组成的预测函数中，样本标签被预测为1的概率为：

---

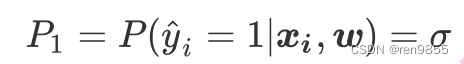
    样本i在由特征向量 和权重向量 组成的预测函数中，样本标签被预测为0的概率为：

---

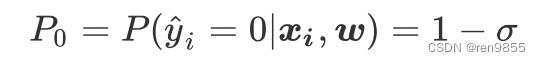
    当P₁的值为1的时候，代表样本i的标签被预测为1，当P₀的值为1的时候，代表样本i的标签被预测为0。P₁与P₀ 相加是一定等于1的.

将两种概率联合:
单个的概率:

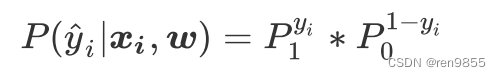
将P₁和P₂替换,加上符号得到所有样本的概率:

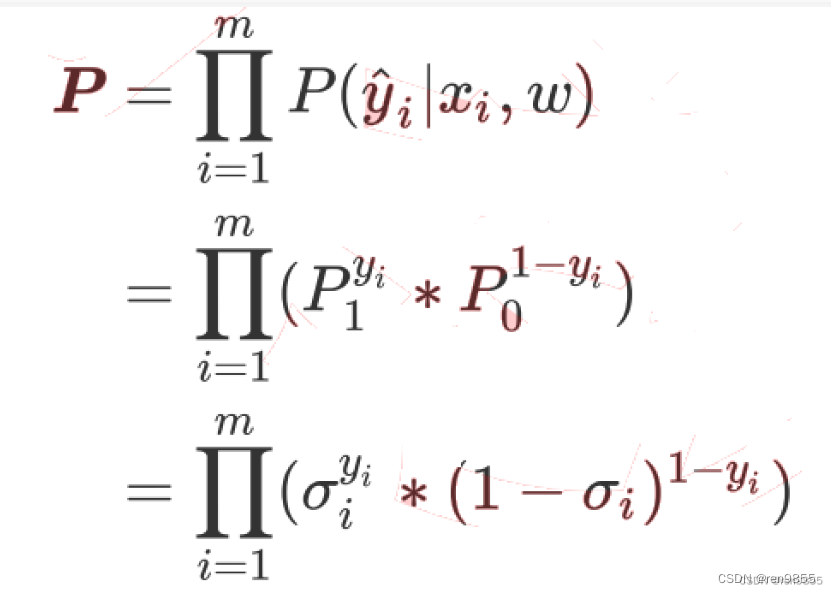
对该概率P取以e为底的对数:

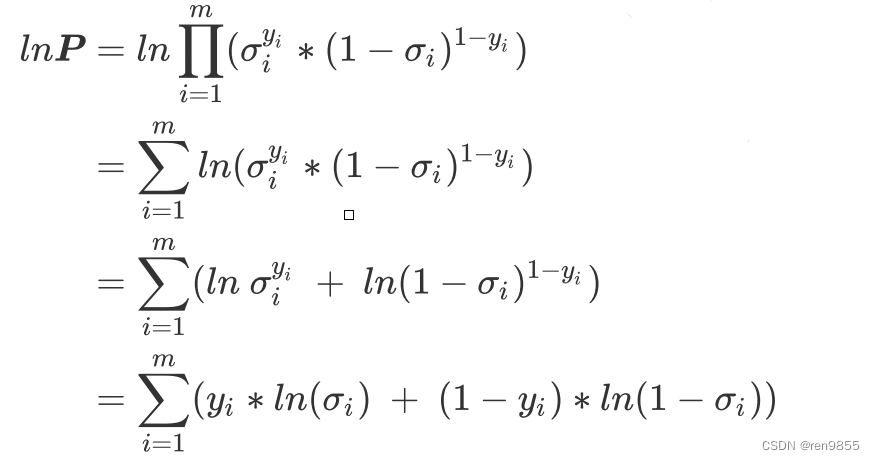
我们将极大值转换为极小值,因此我们对lnP取负:

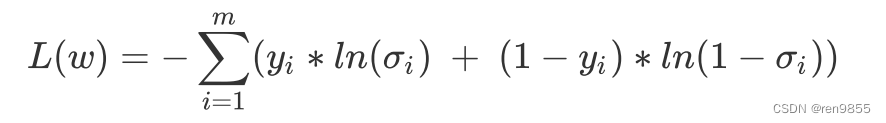
3.4 用tensor实现二分类交叉熵损失

import torch
import time

N = 3*pow(10,3)
torch.random.manual_seed(420)
X = torch.rand((N,4),dtype=torch.float32)
w = torch.rand((4,1),dtype=torch.float32,requires_grad=True)
y = torch.randint(low=0,high=2,size=(N,1),dtype=torch.float32)
zhat = torch.mm(X,w)
sigma = torch.sigmoid(zhat)
Loss = -(1/N)*torch.sum((1-y)*torch.log(1-sigma)+y*torch.log(sigma))

4.多分类交叉熵损失函数

    对于多分类的状况而言，标签不再服从伯努利分布（0-1分布），因此我们可以定义，样本i在由特征向量和权重向量组成的预测函数中，样本标签被预测为类别k的概率为:

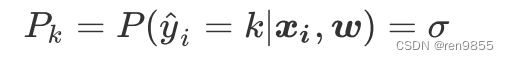
   对于多分类算法而言,σ就是softmax函数返回的对应类别的值。

    假设样本的真实标签为1,我们就希望 P₁最大,同理,如果样本的真实标签为其他值，我们就希望其他值所对应的概率最大。二分类可以使用0和1来分类,如果多分类的标签也可以使用0和1来表示就好了,这样我们就可以继续使用真实标签作为指数的方式,如下图方式进行改变

  原本的真实标签y是含有[1, 2, 3]三个分类的列向量,现在我们把它变成了标签矩阵,每个样本对应一个向量.

---

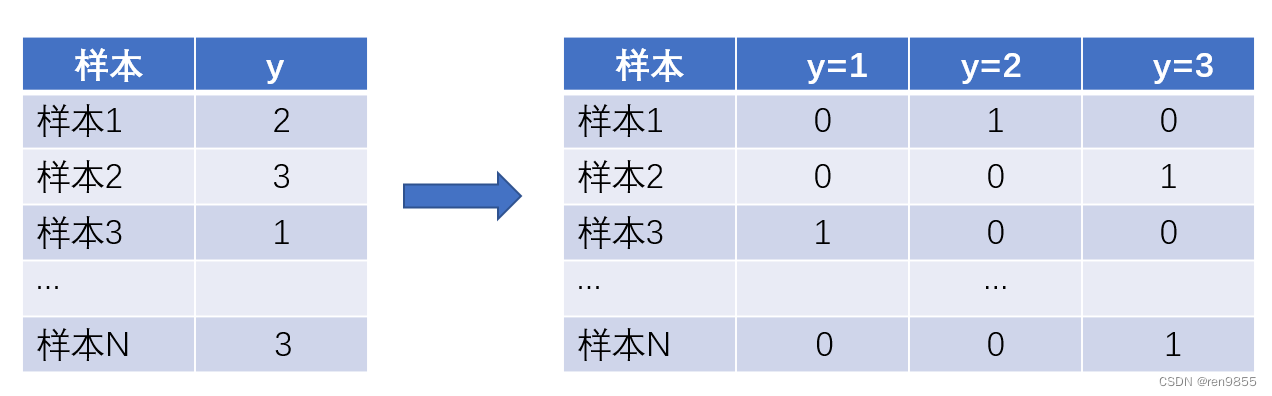
  当我们把标签整合为标签矩阵后,我们就可以将单个样本在总共K个分类情况整合为以下的似然函数

---

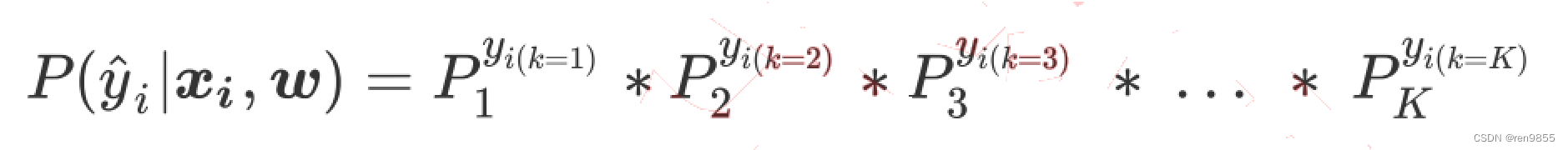
公式简写为:

所有可能的的概率P求和为:

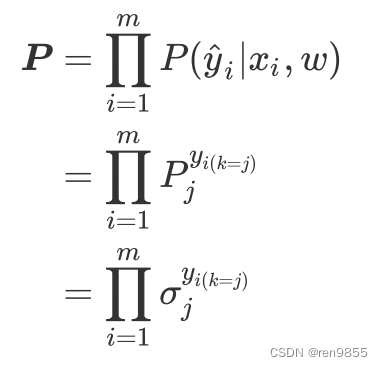
  再对整个公式取负，就得到了多分类状况下的损失函数

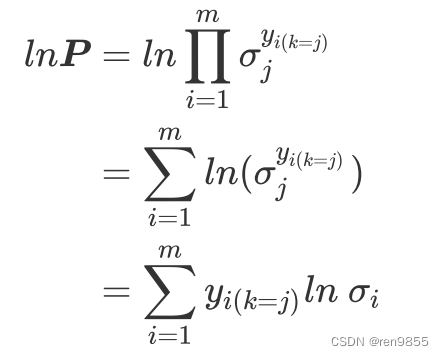
4.1 实现多分类交叉熵损失

import torch
import torch.nn as nn
N = 3*pow(10,2)
torch.random.manual_seed(420)
X = torch.rand((N,4),dtype=torch.float32)
w = torch.rand((4,3),dtype=torch.float32,requires_grad=True)

y = torch.randint(low=0,high=3,size=(N,),dtype=torch.float32)
zhat = torch.mm(X,w)
#从这里开始调用softmax和NLLLoss
logsm = nn.LogSoftmax(dim=1) #实例化
logsigma = logsm(zhat)
criterion = nn.NLLLoss() #实例化
criterion(logsigma,y.long())

输出结果: