目 录
摘 要 I
ABSTRACT II
1绪论 1
1.1选题背景及意义 1
1.2国内外研究现状 1
1.3微积分发展概述 2
1.3.1微积分学的创立 2
1.3.2微积分诞生的重要意义 3
1.3.3微积分理论内容介绍 3
1.3研究主要内容 4
2微积分在金融投资中的应用 5
2.1导数在金融投资中的应用 5
2.1.1导数在金融投资边际分析部分的应用 5
2.1.2导数在弹性理论中的应用 11
2.2极限在金融投资中的应用 14
2.2.1极限解决连续复利问题 14
2.2.2极限在弹性求法中的应用 15
2.3积分在金融投资中的应用 15
2.3.1利用积分性质用来求原函数 16
2.3.2利用积分性质计算消费者剩余 16
3总结 19
参考文献 20
1.3研究主要内容
本文采用数学的思维对拟解决的主要问题进行分析,采用微积分的方式对各个主要问题进行研究。复利与连续复利,债券的价格风险(凸性、久期及修正久期),商品的需求弹性、价格弹性,在公司金融中的边际效应,投资组合中的最优选择,在教学实践中培养学生的建模思想,有助于提高学生的学习积极性。只有学好微积分知识,我们才能对现实中纷繁复杂的经济现象进行剖析与研究,在国家宏观和企业微观的不同层面提出经济政策建议,从而对社会更好的进行服务。
2微积分在金融投资中的应用
微积分在经济领域中的应用,主要是研究在这一领域中出现的一些函数关系,因此必须了解一些经济分析中常见的函数。导数在金融投资中的应用是十分广泛的,因为在金融投资中很多函数里面都有导数的存在才能去进行一些定量分析进而得出最优化的结果。根据导数的一些性质可以为大家解释一些金融投资函数图像的走向问题,为何会出现此种走向等等。同样的在极限的概念基础上面,很多微积分的概念理论得到发展,很多金融投资的知识也得到有效的解决。像一些复利问题,还有用极限方法解决弹性计算问题。积分的应用是由人们在生产生活活动中,为了解决复杂和动态过程的量化累积而引入的。在日常经济活动中,积分的应用也非常广泛,比如求总值(如总成本和总利润等),包括其他变量时间累计的总量等。这些经济活动内容涉及到很多个领域,且函数表达方式都有所不同,但它们的原理都是一样的。这些都是微积分在金融投资中的广泛应用。






微积分在金融投资的应用
news2026/2/12 22:44:07
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/27544.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
Springboot疫苗接种管理系统-JAVA.JSP【数据库设计、源码、开题报告】
摘 要
预防预接种工作实行网络信息化管理,是我国免疫规划工作发展的需要。接种信息实行网络信息化不仅是预防接种工作步入了一个新的台阶,更重要的是解决了多年疫苗接种过程种,免疫接种剂次不清,难以全程有效接种的问题ÿ…
SpringBoot + openFeign实现远程接口调用
SpringBoot服务之间通过openFeign实现远程接口调用
现在的微服务项目不少都使用的是springbootspring cloud构建的项目,微服务之间的调用都离不开feign来进行远程调用。那么我们一个服务需要调用第三方的服务的时候,我们常常可能使用httpclient或者rest…
正大国际期货:2022正大期货在国际市场热度不减的几点原因
2022年国际期货是金融行业重点关注的对象,从今年市场数据中可以看出,正大国际期货之所以还能一如既往领跑,每年交易量都在递增,和正大后台的实力雄厚,坚守合作互赢的理念重大相关,接下来重点说说正大国际越…
【ML-SVM案例学习】svm实现手写数字识别
文章目录前言一、源码分步解析1.引入库2. 设置属性防止中文乱码3.加载数字图片数据4.获取样本数量,并将图片数据格式化5.模型构建6.测试数据部分实际值和预测值获取7.进行图片展示8.把预测错的值的 x值 y值 和y的预测值取出9.通过enumerate,分别拿出x值 …
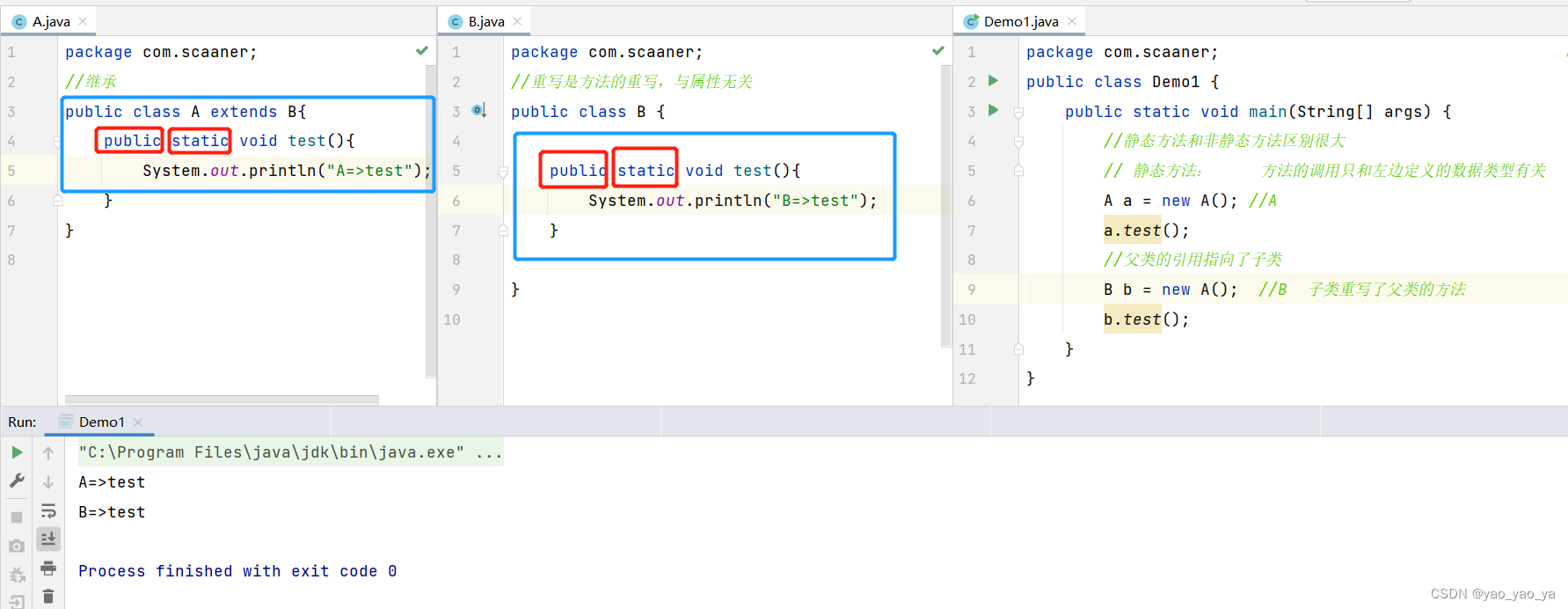
Java的三大特性之继承
封装详见:Java的三大特性之封装 多态详见:Java的三大特性之多态 1.认识继承
继承的本质是对某一批类的抽象,从而实现对显示世界更好的建模。
extends “扩展” 子类是父类的扩展,子类继承了父类,就会有父类的全部方法…
强推这款键盘利器(Keychron),这次我彻底入坑了
嗨喽,大家好。还记得我今年五月份的时候,发布了一篇关于自己使用键盘的文章——>程序猿必备键盘推荐(Keychron),实用炫酷两不误,这篇文章发布后引起了强烈的反响。身边的同学、朋友,包括一些…
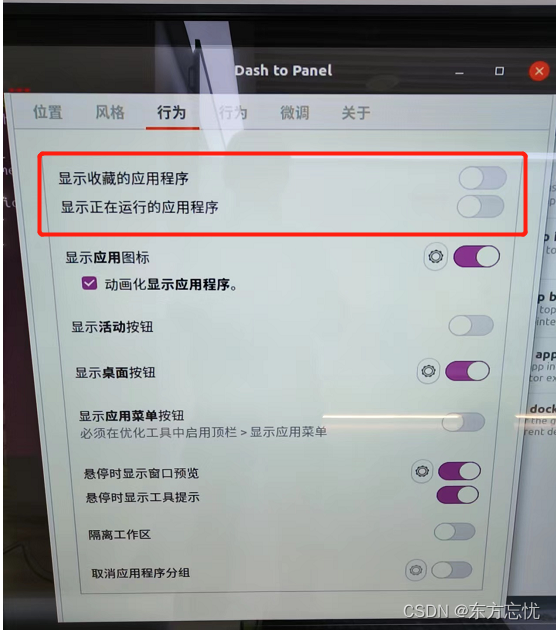
Ubuntu20.4系统隐藏顶栏
注:Ubuntu20.4以上版本安装gnome-tweak-tool可以实现隐藏顶栏了,但20.4还需要安装一下扩展模块,教程如下:
在Ubuntu中有两个扩展工具都支持隐藏顶栏。 1、安装autohidetopbar。
sudo apt install gnome-shell-extension-autohid…
【web】JavaScript——Web APIs笔记小结 dom 样式属性(自定义属性+节点操作部分)
期中考完回来更新了 感觉进度真的好慢T^T,已经摸了快一个月的鱼了qwq!!!
来源:JavaScript基础语法-dom-bom-js-es6新语法-jQuery-数据可视化echarts
目录
⑦H5自定义属性
V.节点操作
①节点层级
※※父级节点
※…
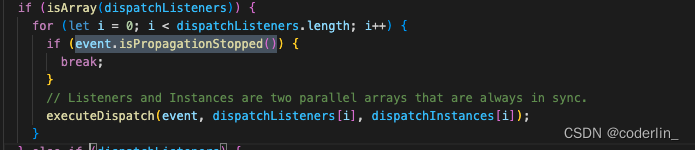
react事件系统(新老版本)
带着问题阅读探索
React 为什么有自己的事件系统?什么是事件合成 ?如何实现的批量更新?事件系统如何模拟冒泡和捕获阶段?如何通过 dom 元素找到与之匹配的fiber?为什么不能用 return false 来阻止事件的默认行为&…
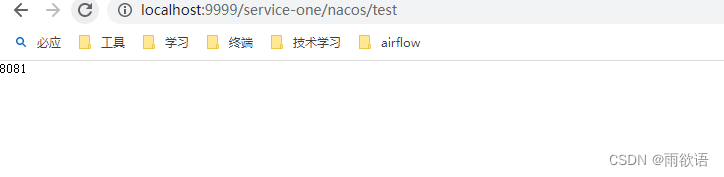
SpringCloudGateway--自动路由映射
目录
一、GateWay项目创建
二、子项目创建
三、测试调用 一、GateWay项目创建 首先启动本地nacos,具体可参考:Nacos Windows安装_雨欲语的博客-CSDN博客 新建工程项目spring_cloud_test,pom引入依赖:
<parent><groupId>org.s…
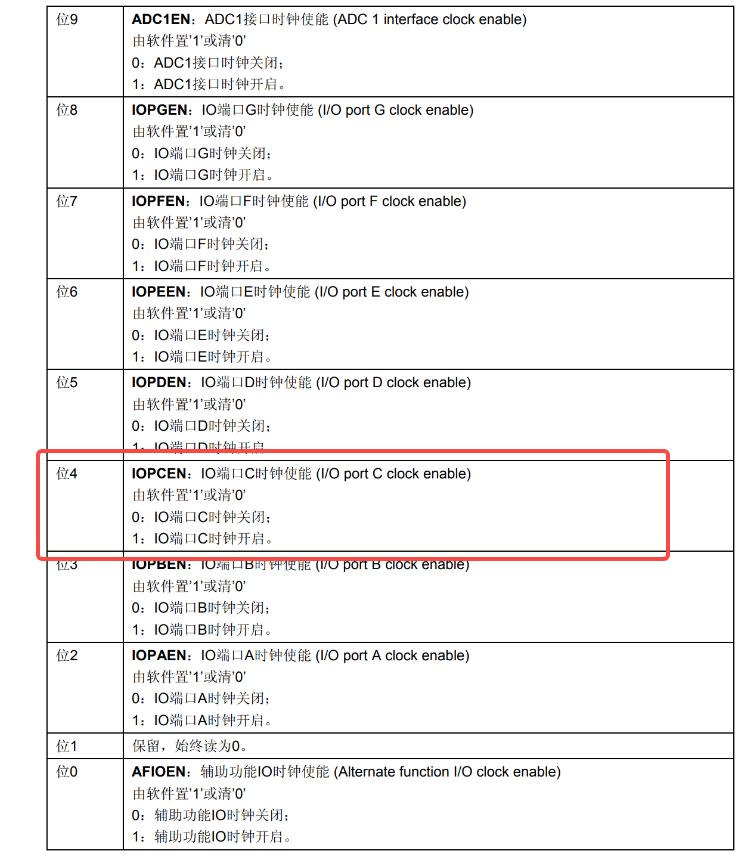
单片机只会调库和复制别人的代码是什么水平?
单片机只会调库和复制别人的代码是什么水平?前言什么是调库?如何不调库点亮一个LED调库与不调库的区别为什么要操作寄存器结语前言 相信对于学习过单片机的同学对于调库这个操作都不陌生,大家都是从调别人的库阶段过来的,今天看到…
便捷记账本小程序+后台管理系统-JAVA【数据库设计、源码、开题报告】
第一章 绪 论
1.1选题背景
互联网是人类的基本需求,特别是在现代社会,个人压力增大,社会运作节奏高,随着互联网的快速发展,用户的需求也越来越高,用户也将越来越多依靠互联网而不是自己获取信息ÿ…
Go:进度条工具库 vbauerster/mpb 简介
文章目录简介核心能力示例单进度条渲染多进度条渲染小结简介
mpb是一个在终端进行进度条渲染的工具库
核心能力
支持多进度条 Multiple Bars: Multiple progress bars are supported支持动态设置进度条总值 Dynamic Total: Set total while bar is running支持动态增加 / 删…
【Unity Shader】屏幕后处理4.0:基于高斯模糊的Bloom
原本打算写高斯模糊和双重模糊两个实现Bloom方法的对比,但两个加在一起篇幅过长,于是拆成两篇文章来进行。
学习前建议应先搞清楚的几个概念
HDRLDRToneMapping几种模糊算法1 高斯模糊实现Bloom
最近一直在学习Unity Shader实现各种后处理效果&#x…
c++ - 第13节 - c++中的继承
1.继承的概念及定义 面向对象三大特性:封装、继承、多态注:面向对象不止这三个特性,还有其他特性,比如反射(Java中的概念)、抽象等封装的理解:(1)将c设计的stack类&#…
记一次艰难的上班历程
我是卢松松,点点上面的头像,欢迎关注我哦!
以下事件均为卢松松真实经历:
早上7点,小区又被静默了,几百号人堵在小区门口。
我不顾病毒传染的风险挤到了小区门口,问原因。
看门的说到&#x…
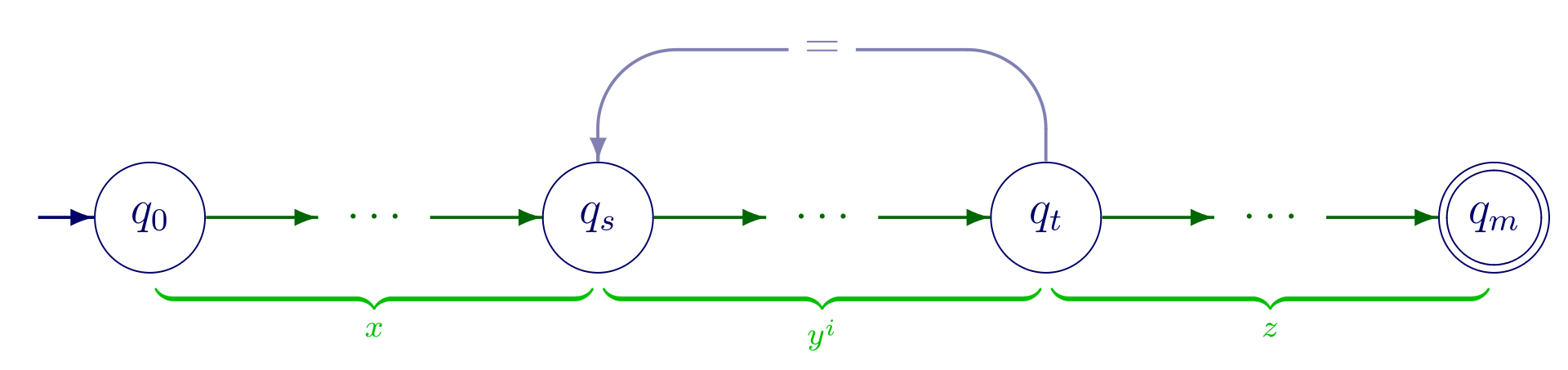
pumping lemma
正规语言版本 LLL是正规语言,则存在整数p≥1p\ge 1p≥1 对于任意长度大于等于ppp的字符串w∈Lw\in Lw∈L,wxyzwxyzwxyz,满足下面3个条件 ∣y∣≥1\left|y\right|\ge 1∣y∣≥1 ∣xy∣≤p\left|xy\right|\le p∣xy∣≤p ∀n≥0,xynz∈L\forall n\ge 0,xy^nz\in L∀n≥…
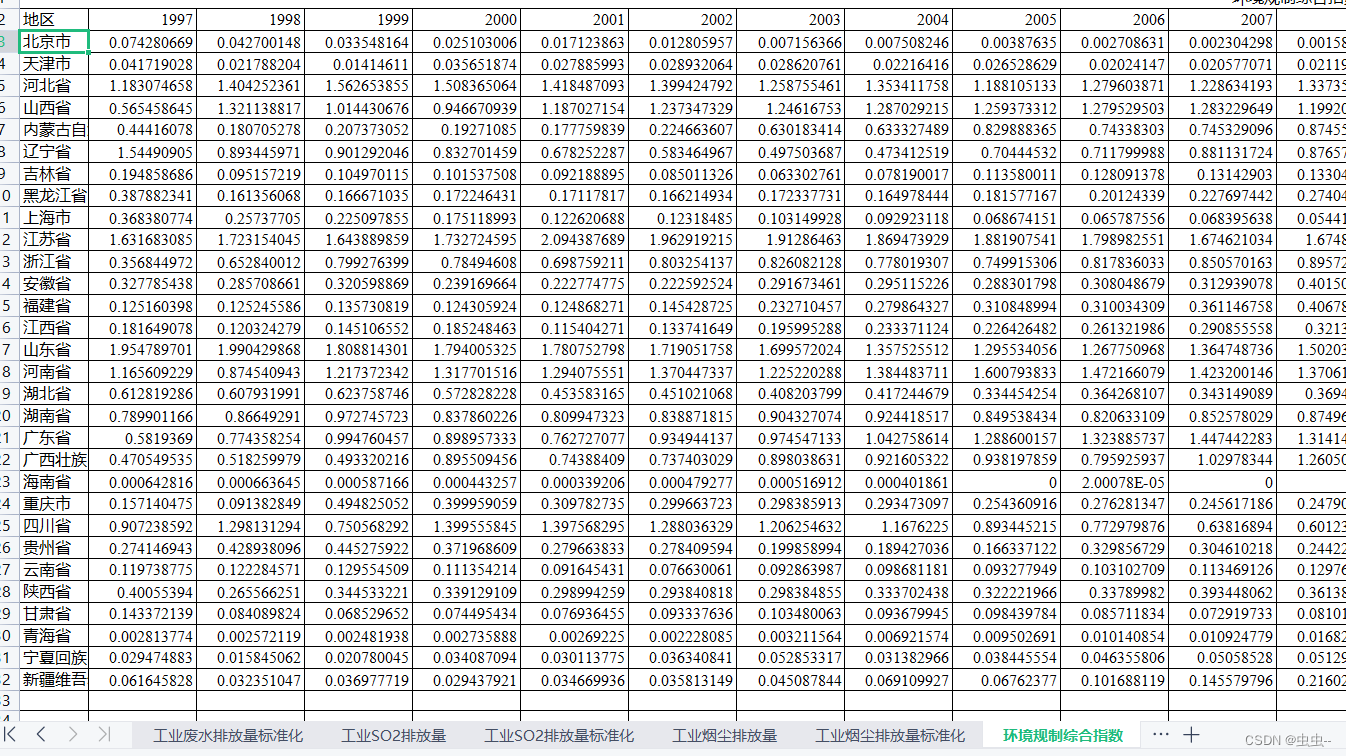
1997-2020年各省三废排放量和熵值法计算的环境规制综合指数(无缺失值)
1997-2020年各省三废排放量和环境规制综合指数
1、包括:30个省份
2、指标包括:工业二氧化硫排放量、工业烟尘排放量和工业废水排放量
环境规制综合指数是由工业废水排放量、工业 SO2 排放量以及工业烟尘排放量计算而来
(表格中有详细的三…
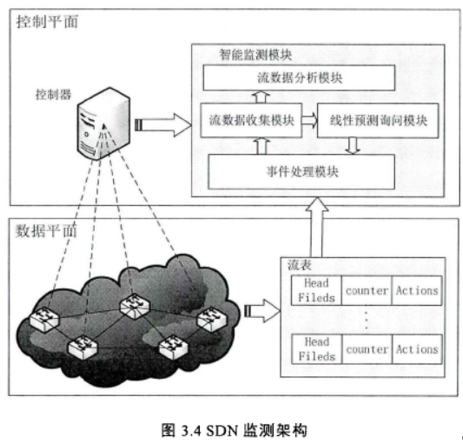
网络流量监测与调度技术研究
网络流量监测与调度技术研究网络流量监测与调度技术研究学习目标:流量监测学习内容:流量监测流量监测的设计框架框架一框架二框架三申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计…
零基础上手unity VR开发【Oculus账号体系准备】
📌个人主页:个人主页 🧀 推荐专栏:Unity VR 开发成神之路 --【着重解决VR项目开发难,国内资料匮乏的问题。从零入门,一步一个脚印,带你搞定VR开发! 😻😻】 Ὅ…