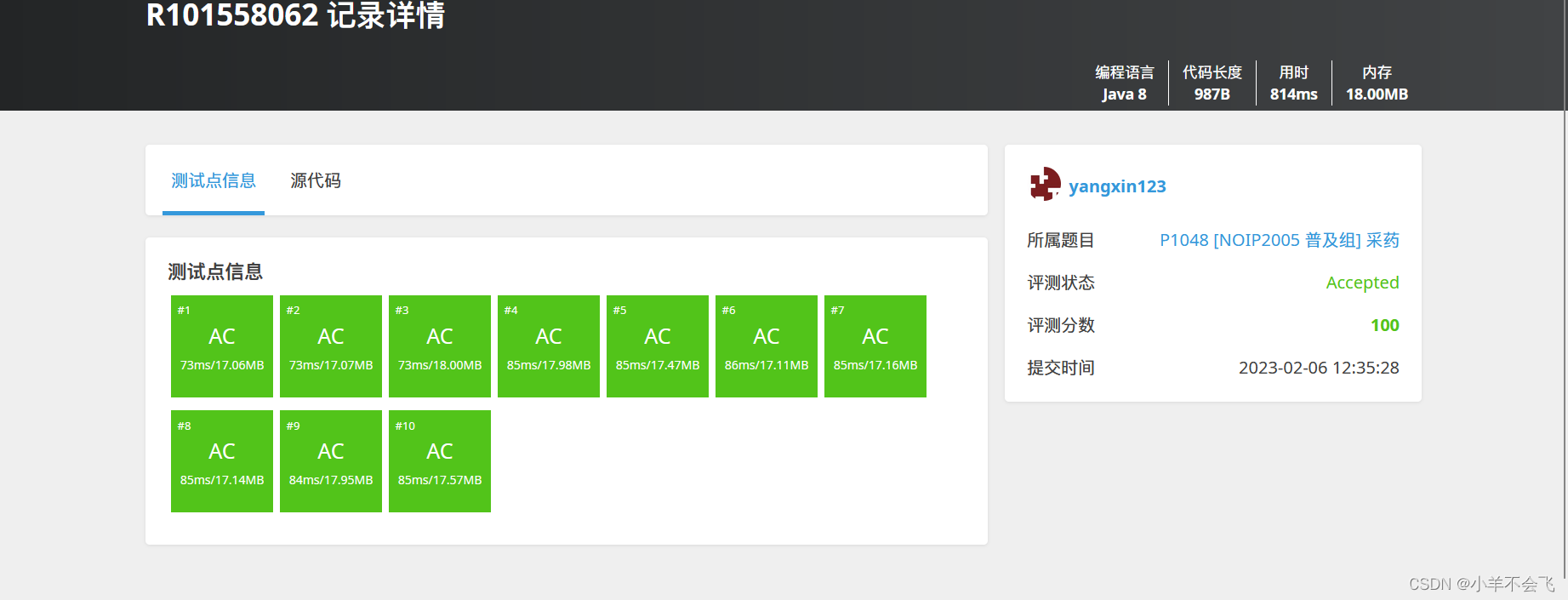
T1：P1048 [NOIP2005 普及组] 采药 - 洛谷

代码：

1、二维Dp：

package 蓝桥算法两周训练营__普及组.Day2_dp;

import java.util.Scanner;

/**
 * @author yx
 * @date 2023-02-05 13:16
 */
public class t1 {
    //    P1048 [NOIP2005 普及组] 采药 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int T=scanner.nextInt();
        int M=scanner.nextInt();
        int[] values=new int[M+1];
        int[] times=new int[M+1];
        for (int i = 1; i <= M; i++) {
            times[i]=scanner.nextInt();
            values[i]=scanner.nextInt();
        }
        int[][] dp=new int[T+1][M+1];
        for (int i = 1; i <= T ; i++) {
            for (int j = 1; j <= M ; j++) {
                if(i<times[j]){
                    //不采第j个草药
                    dp[i][j]=dp[i][j-1];
                }else {
                    //可以不采第j个草药，也可以采，选择最大价值的方案
                    dp[i][j]=Math.max(dp[i][j-1],dp[i-times[j]][j-1]+values[j]);
                }
            }
        }
        System.out.println(dp[T][M]);
    }
}

分析1：

时间T其实对应于背包问题中的总体积T，M对应于物品个数

思路：

1、先依次遍历从背包容量为i（1<=i<=T）开始

2、在不超过背包容量i的前提基础上(i>=times[j])，尽可能地往背包里塞东西

3、如何判断是否要装入物品j呢？我们可以判断不装物品j（dp[i][j-1]）与装入物品j（dp[i-times[j][j-1]]+values[j]）进行比较，取最优的解

2、一维Dp：

package 蓝桥算法两周训练营__普及组.Day2_dp;

import java.util.Scanner;

/**
 * @author yx
 * @date 2023-02-06 16:39
 */
public class t1_01背包_一维 {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int T=scanner.nextInt();
        int M=scanner.nextInt();
        //背包总容量T
        int[] dp=new int[T+1];
        int[] times=new int[M+1];
        int[] values=new int[M+1];
        //背包的体积和价值
        for (int i = 1; i <= M; i++) {
            times[i]=scanner.nextInt();
            values[i]=scanner.nextInt();
        }
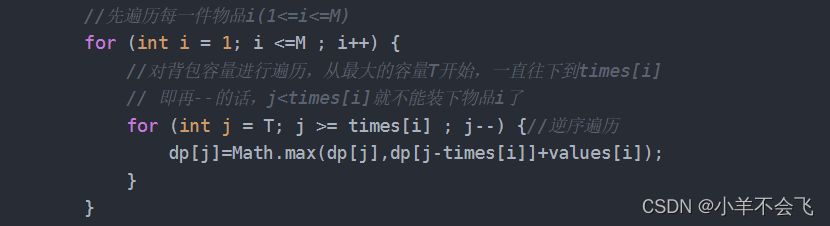
        //先遍历每一件物品i(1<=i<=M)
        for (int i = 1; i <=M ; i++) {
            //对背包容量进行遍历，从最大的容量T开始，一直往下到times[i]
            // 即再--的话，j<times[i]就不能装下物品i了
            for (int j = T; j >= times[i] ; j--) {//逆序遍历
                dp[j]=Math.max(dp[j],dp[j-times[i]]+values[i]);
            }
        }
        System.out.println(dp[T]);
    }
}

分析2：

让我假设现在的背包的容量是 C=10；

物品编号：1   2   31   2   3

物品重量：5   6   45   6   4

物品价值：20 10 1220 10 12

---

直接分析dp数组：

dp：0 0 0 0 0 0 0 0 0 0

i=1:
dp[10] = max(dp[5]+20, dp[10]);
dp[9] = max(dp[4]+20, dp[9]);
dp[8] = max(dp[3]+20, dp[8]);
dp[7] = max(dp[2]+20, dp[7]);
dp[6] = max(dp[1]+20, dp[6]);
dp[5] = max(dp[0]+20, dp[5]);

dp: 0 0 0 0 20 20 20 20 20 20

i=2:
dp[10] = max(dp[6]+4, dp[10]);
dp[9] = max(dp[3]+10, dp[9]);
dp[8] = max(dp[2]+10, dp[8]);
dp[7] = max(dp[1]+10, dp[7]);
dp[6] = max(dp[0]+10, dp[6]);

dp: 0 0 0 0 20 20 20 20 20 20 //看到了没，选10的都被之前的20压下去了

i=3:
dp[10] = max(dp[6]+12, dp[10]);
dp[9] = max(dp[5]+12, dp[9]);
dp[8] = max(dp[4]+12, dp[8]);
dp[7] = max(dp[3]+12, dp[7]);
dp[6] = max(dp[2]+12, dp[6]);
dp[5] = max(dp[1]+12, dp[5]);
dp[4] = max(dp[0]+12, dp[4]);

dp: 0 0 0 12 20 20 20 20 32 32

dp[10] 就是背包容量为 10 的时候的最大价值，就是要求的值了，可以看到，容量大的时候的值取决于容量小的时候的值，从而不断被正确更新，所以用一维 dp 的时候，j 的循环必须是从大到小逆序开始的，逆序，就防止了一个物品放入多次！！！否则...........

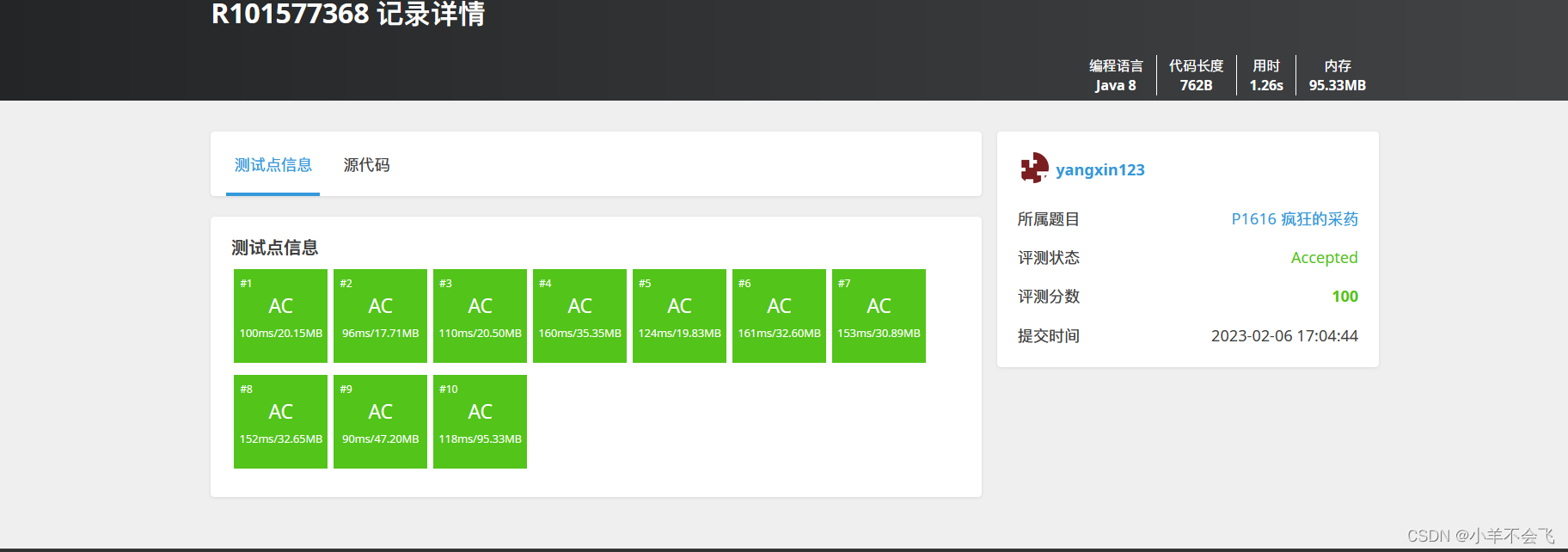
T2：P1616 疯狂的采药 - 洛谷

代码：

package 蓝桥算法两周训练营__普及组.Day2_dp;

import java.util.Scanner;

/**
 * @author yx
 * @date 2023-02-05 13:16
 */
public class t2_完全背包 {
//    ​P1616 疯狂的采药 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)​
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int T=scanner.nextInt();
        int M=scanner.nextInt();
        int[] times=new int[M+1];
        int[] values=new int[M+1];
        //十年IO一场空，不开long long 见祖宗
        long[] dp=new long[T+1];
        for (int i = 1; i <= M; i++) {
            times[i]=scanner.nextInt();
            values[i]=scanner.nextInt();
        }
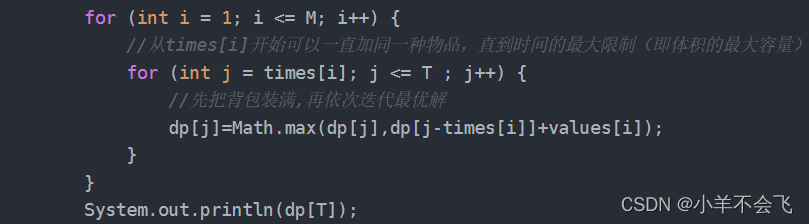
        for (int i = 1; i <= M; i++) {
            //从times[i]开始可以一直加同一种物品，直到时间的最大限制（即体积的最大容量）
            for (int j = times[i]; j <= T ; j++) {
                //先把背包装满,再依次迭代最优解
                dp[j]=Math.max(dp[j],dp[j-times[i]]+values[i]);
            }
        }
        System.out.println(dp[T]);
    }
}

分析：

递推式：

思想：先把背包尽可能装满，再依次迭代最优解

首先dp数组初始化全为0：给定物品种类有4种，包最大体积为5，数据来源于题目的输入
v[1] = 1, w[1] = 2
v[2] = 2, w[2] = 4
v[3] = 3, w[3] = 4
v[4] = 4, w[4] = 5

i = 1 时： j从v[1]到5
dp[1] = max(dp[1],dp[0]+w[1]) = w[1] = 2 (用了一件物品1）
dp[2] = max(dp[2],dp[1]+w[1]) = w[1] + w[1] = 4（用了两件物品1）
dp[3] = max(dp[3],dp[2]+w[1]) = w[1] + w[1] + w[1] = 6（用了三件物品1）
dp[4] = max(dp[4],dp[3]+w[1]) = w[1] + w[1] + w[1] + w[1] = 8（用了四件物品1）
dp[5] = max(dp[3],dp[2]+w[1]) = w[1] + w[1] + w[1] + w[1] + w[1] = 10（用了五件物品）

i = 2 时：j从v[2]到5
dp[2] = max(dp[2],dp[0]+w[2]) = w[1] + w[1] = w[2] =  4（用了两件物品1或者一件物品2）
dp[3] = max(dp[3],dp[1]+w[2]) = 3 * w[1] = w[1] + w[2] =  6（用了三件物品1，或者一件物品1和一件物品2）
dp[4] = max(dp[4],dp[2]+w[2]) = 4 * w[1] = dp[2] + w[2] =  8（用了四件物品1或者，两件物品1和一件物品2或两件物品2）
dp[5] = max(dp[5],dp[3]+w[2]) = 5 * w[1] = dp[3] + w[2] =  10（用了五件物品1或者，三件物品1和一件物品2或一件物品1和两件物品2）

i = 3时：j从v[3]到5
dp[3] = max(dp[3],dp[0]+w[3]) = dp[3] = 6 # 保持第二轮的状态 
dp[4] = max(dp[4],dp[1]+w[3]) = dp[4] = 8 # 保持第二轮的状态 
dp[5] = max(dp[5],dp[2]+w[3]) = dp[4] = 10 # 保持第二轮的状态

i = 4时：j从v[4]到5
dp[4] = max(dp[4],dp[0]+w[4]) = dp[4] = 10 # 保持第三轮的状态
dp[5] = max(dp[5],dp[1]+w[4]) = dp[5] = 10 # 保持第三轮的状态

总结：

一维01背包：

从最大容量T开始到第i件物品容量times[i]，逆序遍历，没有重复，是01背包

一维完全背包：

从第i件物品容量times[i]开始到最大容量T，正序遍历，有重复，是完全背包

课后习题

T3：1015. 摘花生 - AcWing题库

T4：P1077 [NOIP2012 普及组] 摆花 - 洛谷