电子技术——IC偏置-电流源、电流镜、电流舵

IC偏置设计基于恒流源技术。在IC中的一个特定的区域，会生成一个精确的DC电流，这称为 参考电流 ，之后通过电流镜复制到各个所需支路，并且通过电流舵进行电流转向。这项技术为IC的多级放大器提供了稳定精确的电流。

基本MOSFET恒流源

下图展示了一个MOSFET恒流源：

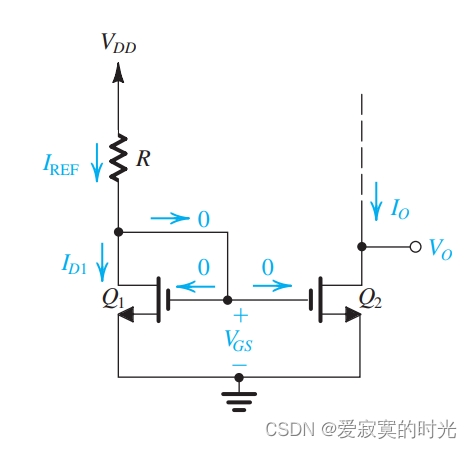
图中关键的部件是晶体管 $Q_1$ ，它的漏极和栅极相连。因此 $Q_1$ 是永远工作在饱和区的，因此饱和电流为：

$$I_{D1}=\frac{1}{2}{k}_n^{\prime }(W/L{)}_1(V_{GS}-V_{tn}{)}^2$$

$Q_1$ 通过 $V_{DD}$ 和 $R$ 提供电压，电压源和电阻通常处在IC之外。因为栅极电流为零，因此：

$$I_{D1}=I_{REF}=\frac{V_{DD}-V_{GS}}{R}$$

通过上述两个式子，通过条件 $R$ 的阻值就可以获得想要的参考电流。

现在考虑晶体管 $Q_2$ 它和 $Q_1$ 具有相同的 $V_{GS}$ ，如果我们假设 $Q_2$ 处在饱和模式下，则输出电流为：

$$I_O=I_{D2}=\frac{1}{2}{k}_n^{\prime }(W/L{)}_2(V_{GS}-V_{tn}{)}^2$$

参考电流和输出电流存在比例关系：

$$\frac{I_O}{I_{REF}}=\frac{(W/L{)}_2}{(W/L{)}_1}$$

这是一个有趣的结果，输入输出电流只和晶体管的尺寸比例有关系，也就是说，IC设计师可以自由设计MOS的尺寸比例，来进行缩放电流，获得不同的恒定电流。在两个晶体管完全相同的情况下，输入输出电流相等。因此这个电路也称为 电流镜 。

下图展示了电流镜更一般的情况：

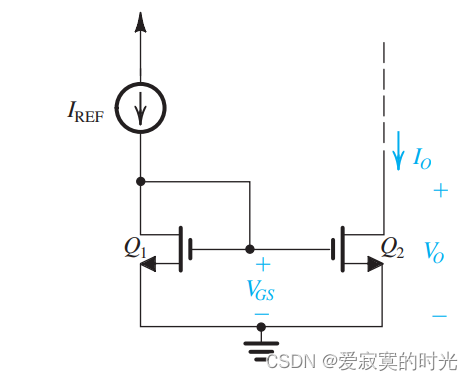
输入电流为 $I_{REF}$ 输出电流通过晶体管尺寸比例调节。晶体管管尺寸比例也称为 电流增益 或是 电流传导比 。

在上述的描述中， $Q_2$ 处在饱和区是电流镜生效的必要条件，为了保证这个条件，必须满足：

$$V_O\ge V_{GS}-V_{tn}$$

换句话说：

$$V_O\ge V_{OV}$$

这里 $V_{OV}$ 是 $Q_1$ 的过驱动电压。

如果我们将MOS的沟道长度调制效应考虑进来，也就是电阻 $r_o$ 。考虑下面的情况，假设 $Q_1$ 和 $Q_2$ 完全相同，那么只有在电压 $V_O=V_{GS}$ 的时候，电流 $I_O=I_{REF}$ 否则随着 $V_O$ 的增加，电流 $I_O$ 也会增加。如图：

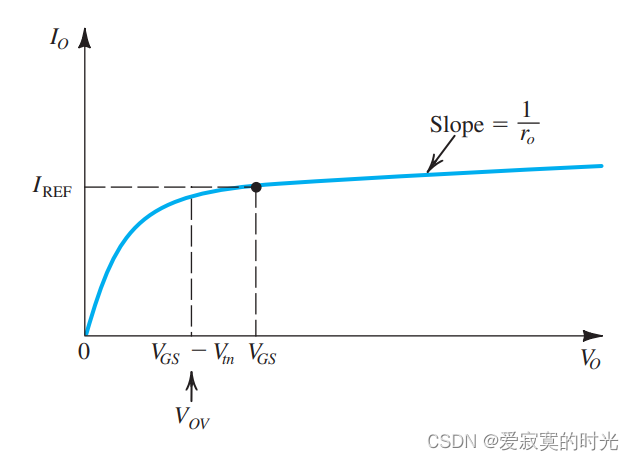
此时 $Q_2$ 表现出有限的输出阻抗：

$$R_O\equiv \frac{\Delta V_O}{\Delta I_O}=r_{o2}=\frac{V_{A2}}{I_O}$$

通常情况下 $V_{A2}$ 即厄尔利电压，与沟道的长度成正比，因此想要获取较大的输出阻抗，就要增大MOS的沟道的长度。最终，输出电流的公式为：

$$I_O=\frac{(W/L{)}_2}{(W/L{)}_1}{I}_{REF}(1+\frac{V_O-V_{GS}}{V_{A2}})$$

MOS 电流舵电路

我们之前提到过，一旦基准电流被生成，电流镜通过拷贝电流给不同的IC元件。电流镜本身就可以实现电流舵功能。如图：

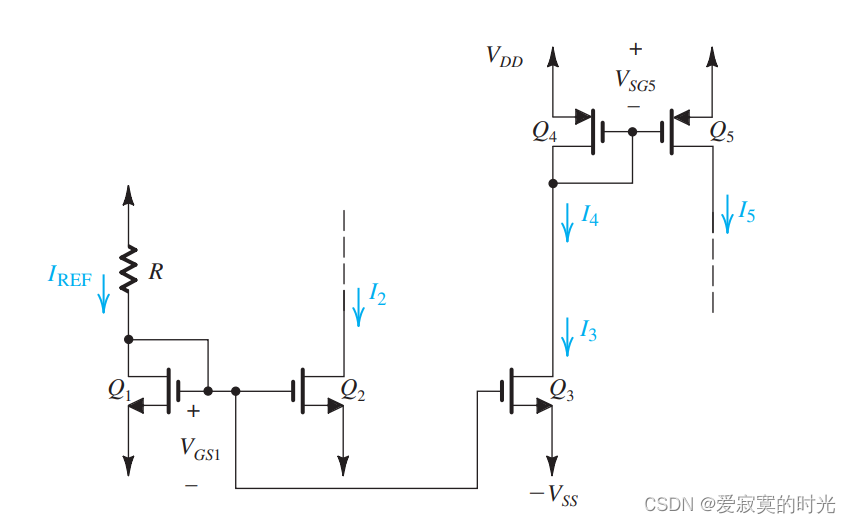
晶体管 $Q_1$ 负责对基准电流进行采样。晶体管 $Q_2$ 和 $Q_3$ 分别是电流镜的两个输出端。

观察这个电路，由 $Q_3$ 生成的电路 $I_3$ 继续供给PMOS电流镜 $Q_4$ 和 $Q_5$ 。

由 $Q_2$ 生成的电流可以给源极跟随器提供偏置，如下图：

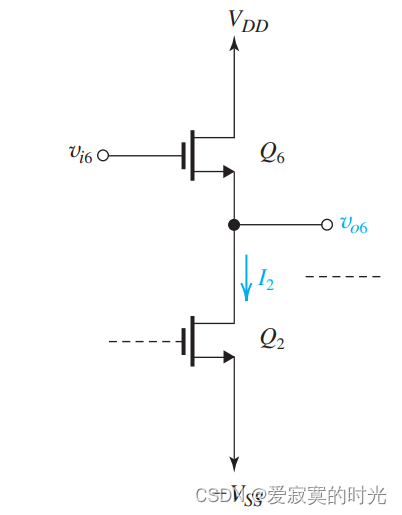
由 $Q_5$ 提供的电流可以给共源极放大器提供偏置，如图：

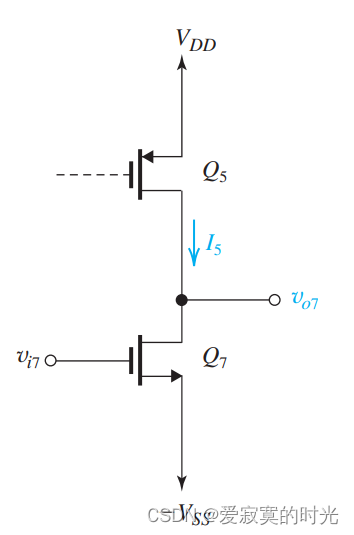
最终，根据电流不同的方向，我们发现，晶体管 $Q_2$ 的作用是从外拉电流到电压源。而晶体管 $Q_5$ 的作用是从电压源往出推电流。我们根据电流源能提供电流的方向，称 $Q_2$ 为 电流阱 而称 $Q_5$ 为 电流源 。在IC设计中，两种电流源都会交替使用，以适应不同的放大器偏置。

下图是两种电流源的抽象表示：

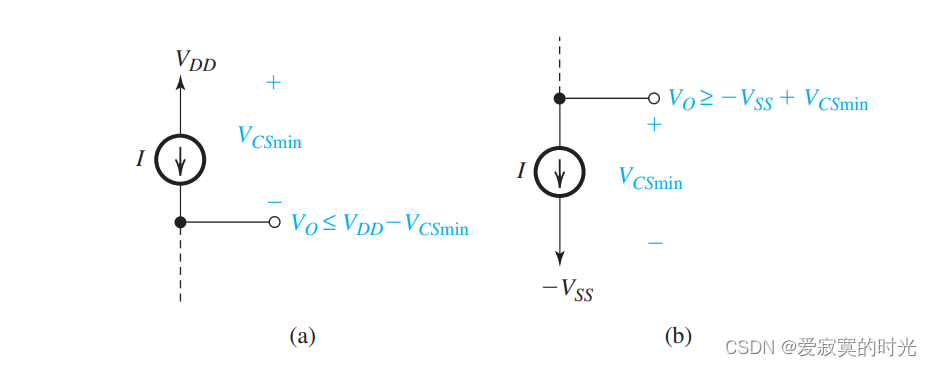
其中 $V_{CSmin}$ 是电流源生效的极限条件。

BJT电路

基本的BJT电流镜如下图所示：

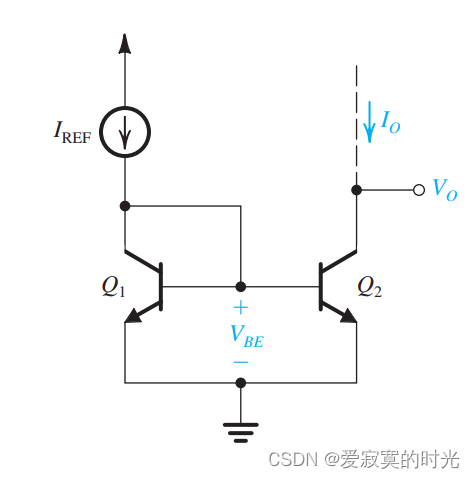
这个电路很像MOS电流源，因为BJT的基极电流不在是零，因此电流的传导特性会与MOS有些不同。

首先我们假设 $\beta$ 足够大基极电流为零的情况，此时 $Q_1$ 永远工作在主动模式下，假设 $Q_2$ 也工作在主动模式下， $Q_1$ 和 $Q_2$ 具有相同的 $V_{BE}$ ，假设 $Q_1$ 和 $Q_2$ 完全匹配，更进一步的，两个晶体管的EBJ截面积完全相同，此时 $I_S$ 相同，可以保证 $I_O=I_{R}EF$ 。

为了获得一般情况下的电流的传导比，记为 $m$ ，也就是：

$$I_O=m{I}_{REF}$$

电流传导比由下面的方程给出：

$$\frac{I_O}{I_{REF}}=\frac{I_{S2}}{I_{S1}}=\frac{S_{Q2}}{S_{Q1}}$$

其中 $\frac{S_{Q2}}{S_{Q1}}$ 是两个晶体管的EBJ的截面积之比，另外，如果 $m$ 是整数，则可以将 $Q_2$ 看做是 $m$ 个 $Q_1$ 并联组成 $Q_2$ 的输出端。

接下来我们考虑有限 $\beta$ 对电流传导比造成的影响。为了方便分析，我们假设 $Q_1$ 与 $Q_2$ 完美匹配，如图：

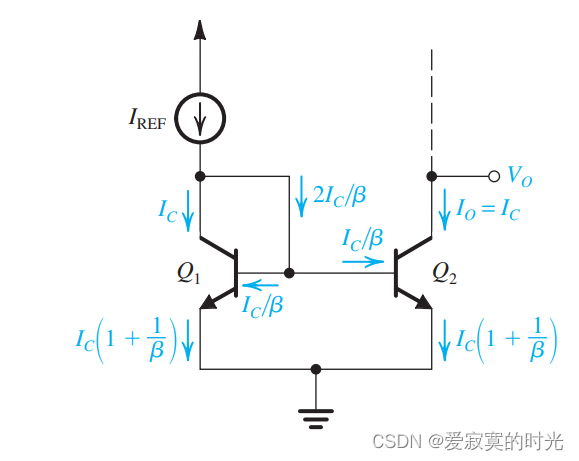
关键是一点是，因为 $Q_1$ 与 $Q_2$ 完美匹配，所以具有相同的 $V_{BE}$ ，也就具有相同的基极电流，则如图所示，参考电流的关系为：

$$I_{REF}=I_C+2I_C/\beta =I_C(1+\frac{2}{\beta })$$

因为 $I_O=I_C$ 所以电流传导比为：

$$\frac{I_O}{I_{REF}}=\frac{I_C}{I_C(1+\frac{2}{\beta })}=\frac{1}{1+2/\beta }$$

当 $\beta$ 趋于无穷大的时候，电流传导比无限接近于一。因此，基极电流或者说是 $\beta$ 是BJT电流镜误差的主要原因。若引入 $m$ 的话，则电流传导比变为：

$$\frac{I_O}{I_{REF}}=\frac{m}{1+(m+1)/\beta }$$

读者可以自行证明。与MOS相同，BJT也存在 $R_O$ ：

$$R_O\equiv \frac{\Delta V_O}{\Delta I_O}=r_{o2}=\frac{V_{A2}}{I_O}$$

考虑所有以上因素，最终的输出电流公式为：

$$I_O=I_{REF}\frac{m}{1+(m+1)/\beta }(1+\frac{V_O-V_{BE}}{V_{A2}})$$

接下来，我们可以构建基于BJT的一个简易电流源，如下图：

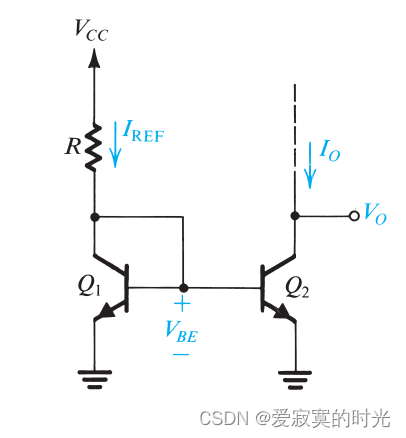
参考电流为：

$$I_{REF}=\frac{V_{CC}-V_{BE}}{R}$$

这里 $V_{BE}$ 是理想BJT中EBJ电压，通常带入 0.7V 。输出电流为：

$$I_O=I_{REF}\frac{1}{1+2/\beta }(1+\frac{V_O-V_{BE}}{V_{A2}})$$

输出阻抗为：

$$R_O=r_{o2}\simeq \frac{V_A}{I_O}\simeq \frac{V_A}{I_{REF}}$$

同样BJT也有相同的电流舵结构，如图：

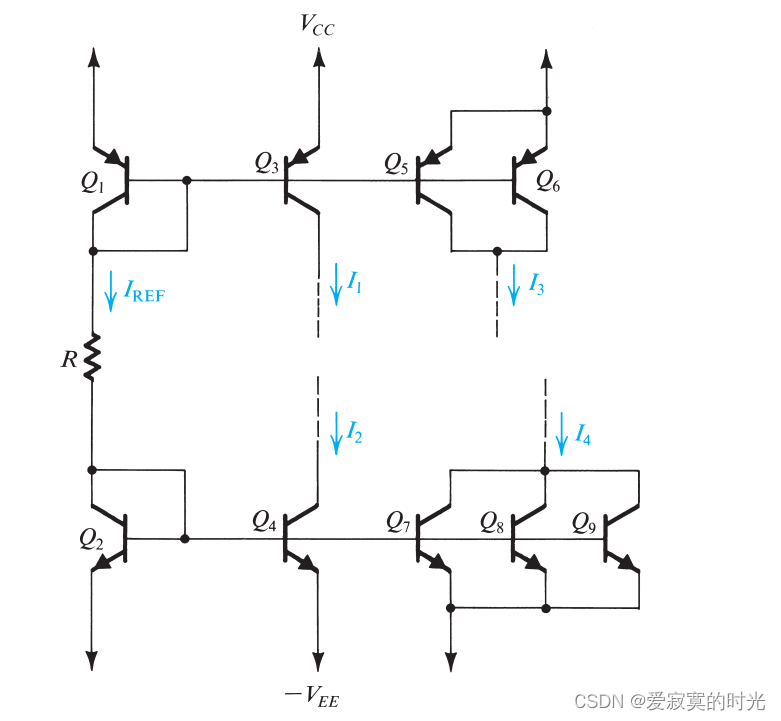
电阻 $R$ 被电流镜 $Q_1$ 和 $Q_2$ 共同作用，因此参考电流为：

$$I_{REF}=\frac{V_{CC}+V_{EE}-V_{EB1}-V_{EB2}}{R}$$

为了方便分析，我们忽略基极电流以及厄尔利电压的作用，以及各个晶体管都是完美匹配的。晶体管 $Q_3$ 作为电流源向外从电压源推电流 $I_1$ ，只要保证集电极电压 $V_C$ 小于 $V_{CC}-0.3V$ ，否则电流镜会失效。

为了生成两倍的 $I_{REF}$ ，我们可以并联两个晶体管 $Q_5$ 和 $Q_6$ ，此时 $I_3=2I_{REF}$ ，这等效于一个EBJ面积是 $Q_1$ 两倍的的BJT。

$Q_4$ 是电流阱，其中集电极电压不低于 $-V_{EE}+0.3V$ 。另外 $I_4=3I_{REF}$ 。

最后一点，由于基极电流是BJT电流镜的主要误差因素，我们可以想办法降低基极电流的大小，这种方案被称为 基极电流补偿 。如下图的电路：

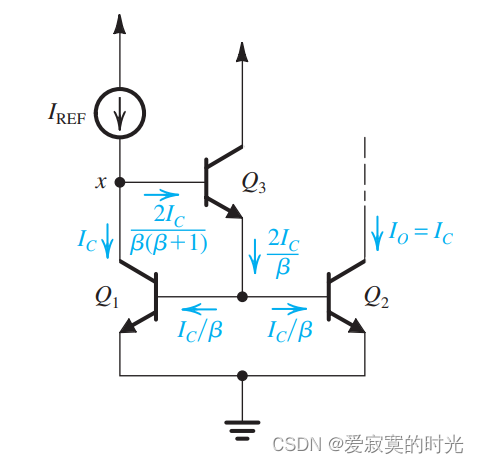
我们在 $Q_1$ 的基极和集电极直接引入BJT $Q_3$ 。此时流向基极的总电流如图所示为：

$$I_{B3}=\frac{2I_C}{\beta (\beta +1)}$$

此时参考电流的关系为：

$$I_{REF}=I_C[1+\frac{2}{\beta (\beta +1)}]$$

电流的传导比为：

$$\frac{I_O}{I_{REF}}=\frac{1}{1+2/({\beta }^2+\beta )}\simeq \frac{1}{1+2/{\beta }^2}$$

这表明， $\beta$ 从原来变为了 ${\beta }^2$ 这是一个巨大的改进。但不幸的是，输出电阻还是原来的 $r_o$ 并没有得到改进。最后一点，如果要手动生成参考电流，可以将 $x$ 端通过电阻 $R$ 接入电压源 $V_{CC}$ 此时：

$$I_{REF}=\frac{V_{CC}-V_{EB1}-V_{BE3}}{R}$$

电流镜的小信号模型

电流镜除了为放大器提供偏置，有时候也作为电流放大器使用，此时我们就需要探究电流镜在小信号下的情况。

下图是一个MOS小信号电流放大器，信号电流 $i_i$ 叠加在 $I_{D1}$ 上。

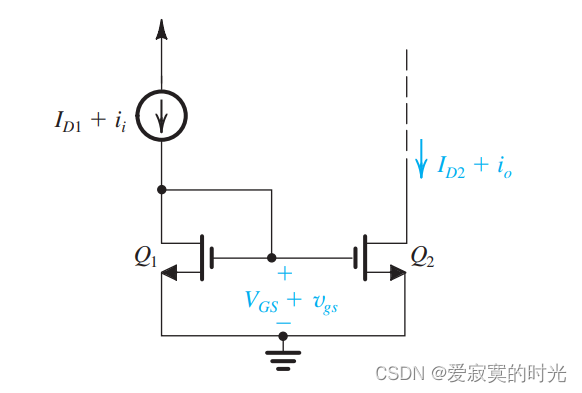
将两个MOS使用混合 $\pi$ 模型等效替代后得到：

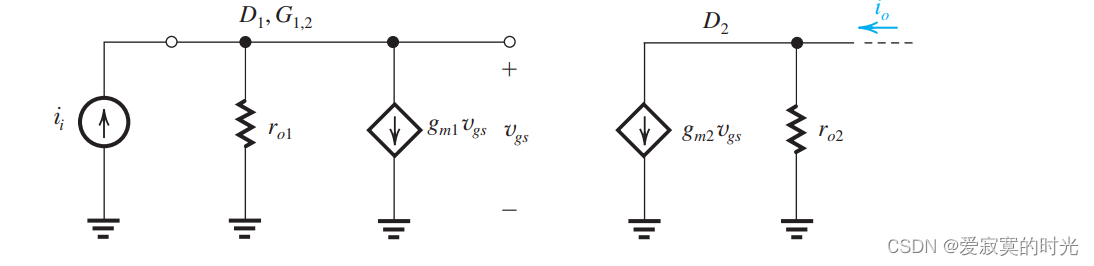
观察到控制电压 $v_{gs}$ 直接作用在受控源 $g_{m1}{v}_{gs}$ 因此，可以使用等效电阻替换 $Q_1$ 得到：

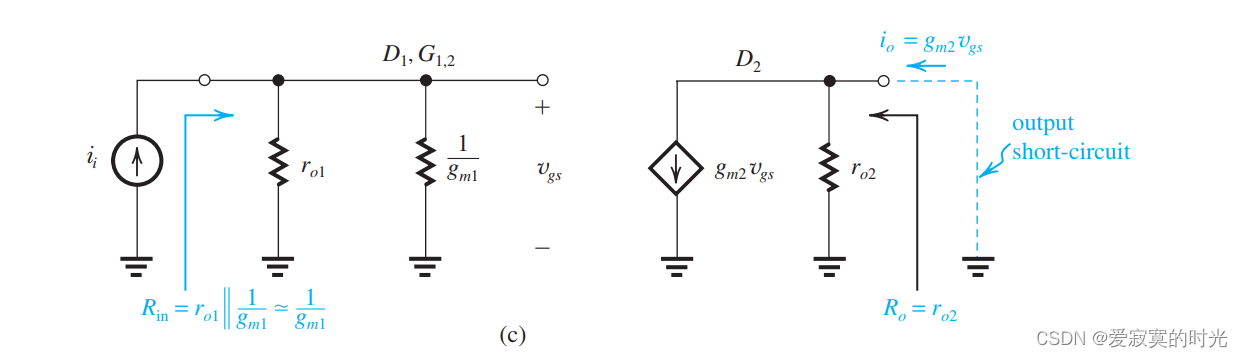
通过这个电路我们可以得到：

$$R_{in}=r_{o1}||\frac{1}{g_{m1}}\simeq \frac{1}{g_{m1}}$$

$$R_o=r_{o2}$$

电流增益为：

$$A_{is}\equiv \frac{i_o}{i_i}{|}_{v_{d2}=0}=\frac{g_{m2}{v}_{gs}}{i_i}\simeq \frac{g_{m2}{i}_i/g_{m1}}{i_i}=\frac{g_{m2}}{g_{m1}}$$

带入 $g_m={\mu }_n{C}_{ox}(W/L)V_{OV}$ ，假设两端拥有 $V_{OV}$ 相同的偏置条件，因此：

$$A_{is}=\frac{(W/L{)}_2}{(W/L{)}_1}$$

与DC的电流传导比一致，这说明，DC操作和小信号操作保持一致，这证明了MOS电流镜的绝佳的线性性质。

MOS电流镜是一个非常不错的电流放大器，他具有相对低的输入阻抗 $1/g_{m1}$ 和一个相对高的输出阻抗 $r_{o2}$ ，并且放大系数只由MOS本身长宽比决定而和DC偏置无关。

同样的分析方法适用于BJT电流放大器分析。