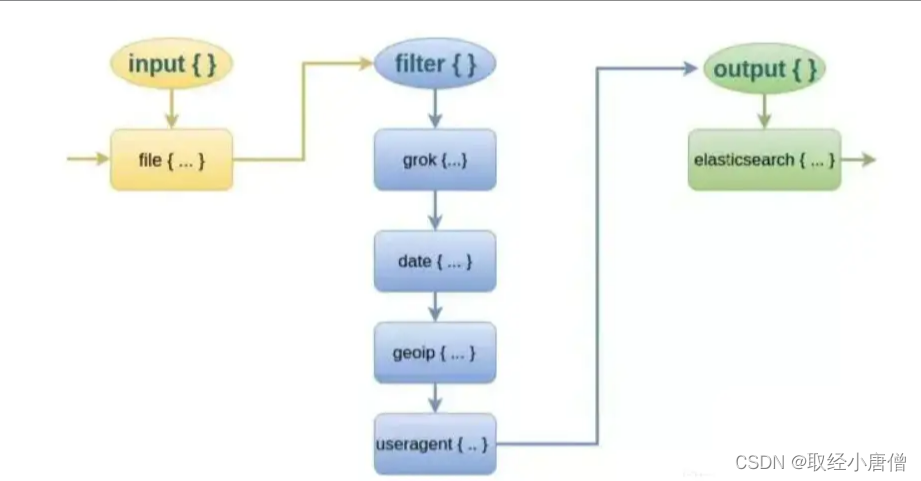
此文转自知乎的jinjin 傅里叶变换的四种形式 - 知乎

       傅里叶变换是信号的一种描述方式，通过增加频域的视角，将时域复杂波形表示为简单的频率函数，获得时域不易发现的与信号有关的其他特征。

       根据时间域信号x自变量的不同，可以将信号分为连续信号x(t)和离散序列x[n]，根据信号周期性不同，又可以将信号分为周期性和非周期性的，所以待分析的信号类型有四种形式，也就产生了四种不同形式的傅里叶变换。

	连续	离散
周期	第一类	第三类
非周期	第二类	第四类

1.周期性连续信号——傅里叶级数Fourier Series（FS）

2.非周期性连续信号——傅里叶变换Fourier Transform（FT）

3.周期性离散信号——离散傅里叶级数（Discrete Fourier Series）DFS

4.非周期性离散信号——离散时域傅里叶变换（Discrete Time Fourier Transform）DTFT

1.连续信号的傅里叶分析

1.1傅里叶级数（FS）

傅里叶级数是将周期连续信号用一组谐波函数表示出来。（一个小结论，周期性导致另一个域的离散型）

对于下面这个谐波函数 x(t)=∑k=−∞∞X(kΩ0)ejkΩ0t ，可以解出 X(kΩ0)=1T∫tt+Tx(t)e−jkΩ0tdt

这里 X(kΩ0) 被称为傅里叶系数（第k次谐波的系数），代表某一谐波分量所占权重，反应第k次谐波幅度的大小，所以在频率坐标轴上 X(kΩ0) 是离散的，间隔是 Ω0 。

1.2傅里叶变换（FT）

傅里叶级数是针对周期函数的，为了可以处理非周期函数，需要傅里叶变换。(主要思路：周期函数可以通过傅里叶级数画出频谱图，增大周期，频率图变得越来越密，当周期区域无穷时（也就是周期延拓的方法），得到傅里叶变换，频谱图变成连续的曲线。)

对于非周期信号 x(t)=12π∫−∞∞X(jΩ)ejΩtdΩ ，傅里叶变换后 X(jΩ)=∫−∞∞x(t)e−jΩtdt （ X(jΩ) 物理意义：频谱密度函数）

2离散信号的傅里叶分析

离散信号的傅里叶分析思路平行于连续信号的傅里叶分析。

2.1离散时域傅里叶变换（DTFT）

在离散系统中，假如x(t)为连续系统信号，要转换成离散系统，需要进行采样，采样频率为fs，采样时间间隔为Ts=1/fs

冲击采样序列为 δs(t)=∑n=−∞∞δ(t−nTs) ，

采样之后的信号为 xs(t)=∑n=−∞∞x(t)δ(t−nTs) .

连续信号的傅里叶变换定义为 X(ω)=∫−∞∞x(t)e−iωtdt ，

则采样后的傅里叶变换为 Xs(ω)=∫−∞∞(∑n=−∞∞x(t)δ(t−nT))e−iωtdt ，

交换积分求和顺序 Xs(ω)=∑n=−∞∞∫−∞∞x(t)δ(t−nTs)e−iωtdt

由于冲激函数的筛选性 ∫−∞+∞f(x)δ(x−x0)dx=f(x0)

得 Xs(ω)=∑n=−∞∞x(nTs)e−iωTs

采样信号是一个序列，第n个采样时间t=nTs，

所以将连续信号傅里叶变换写成这个形式 Xs(ω)=∑n=−∞∞x(n)e−iωTs ,这个式子称为离散时域傅里叶变换。

2.2离散傅里叶级数（DFS）

这里先说一个结论：一个域是周期的则另一个域是离散的，一个域是离散的则另一个域是周期的。

对于周期为N的离散信号x[n]，x[n]=x[n+N]，这是一个周期序列，根据上一行的结论，因为x(n)是离散的，故频谱是周期的，因为x(n)是周期的，故频谱是离散的，所以x(n)得频谱是离散的且是周期的。

对FS: X~(t)=∑k=−∞∞X(kΩ0)ejkΩ0t 进行离散化（ Ω0 =2 π /T，t=nTs，T=NTs，Ω0 =2 π /NTs， tΩ0=2 nπ /N）（其中Ts为采样周期，N为一个周期的采样数）得出

x~(nTs)=∑kX~(kΩ0)ejk2πNTsnTs=∑kX~(kΩ0)ej2πNnk

Ωs=2π/Ts=2πN/T=NΩ0

N=ΩsΩ0=2πfs2π/T=2πfs2πf=fsf=TTs=N

由以上分析可知： x~(nTs) 是离散的，周期为N，间隔是Ts， X~(kΩ0) 是离散的，周期为N，间隔是 Ω0 ,

所以各取一个周期求和，有 X(k)=∑n=0N−1x(n)e−j2πNnkk=−∞∼∞x(n)=1N∑k=0N−1X(k)ej2πNnkn=−∞∼∞ 这个就是离散傅里叶级数（DFS）。

3小结