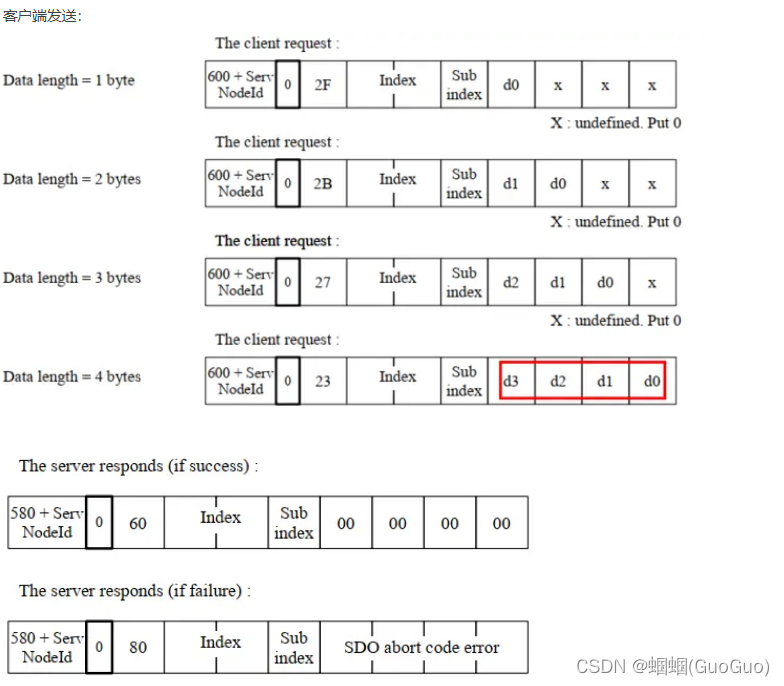
文章目录
- 前言
- 一、如何估计参数
- 二、二分类原生代码实现
- 三、sklearn实现模型
- 总结
前言
-
学习笔记
-
学习视频:https://www.bilibili.com/video/BV1rB4y1v7dA/?spm_id_from=333.788&vd_source=af83080eba7b379d3fda36e341bdb195
-
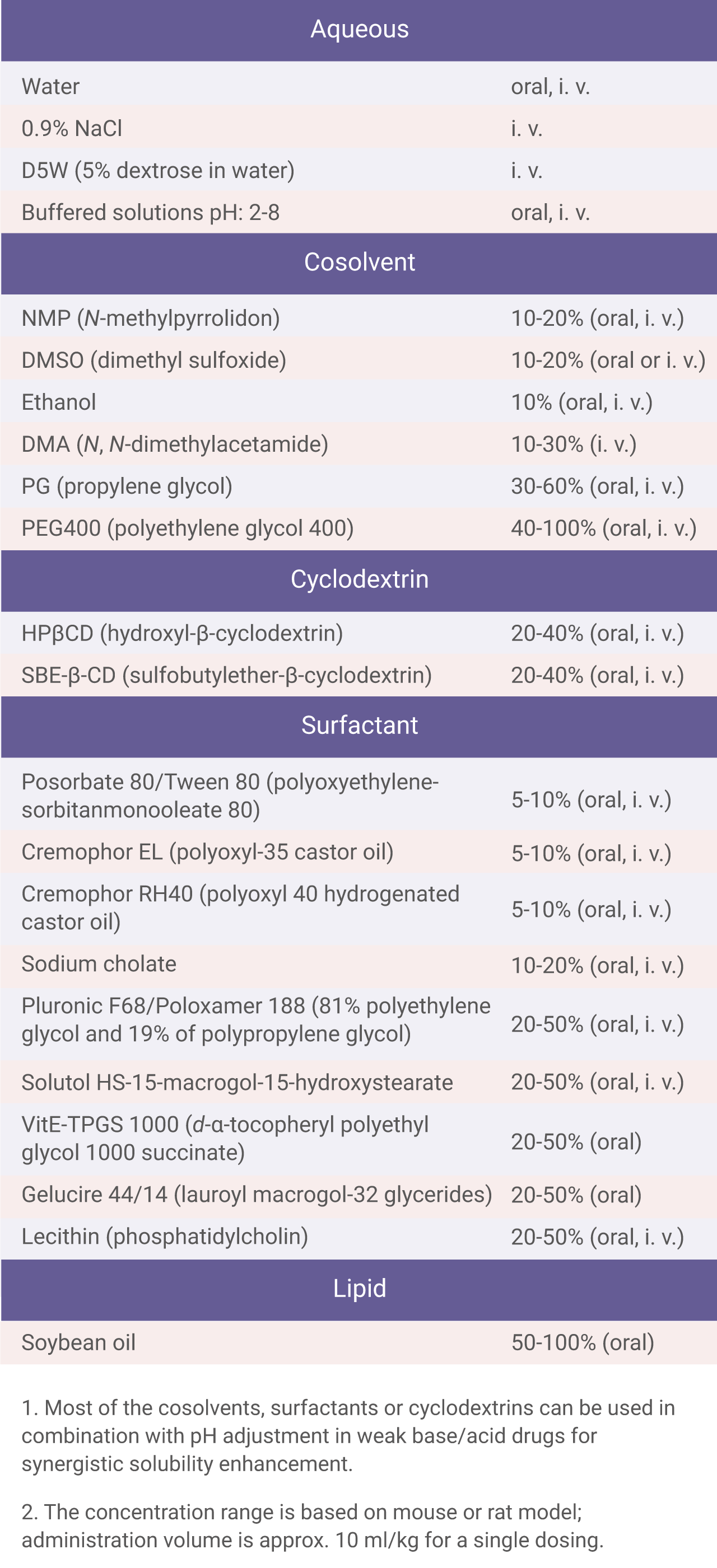
使用高斯混合模型的原因:
-
模型可能总体不属于高斯模型分布
-
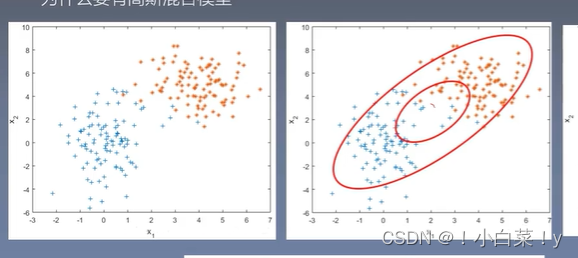
将数据分为两个高斯模型 再将他们混合起来
-
- 混合公式:

其中:
Π 该不同高斯模型对于整个模型所占的权重
N(μ,σ) 不同的高斯模型
-
单个模型公式:
-
一维特征

其中:
μ 是已知数据集的均值
σ 是已知数据集的方差 -
多维特征
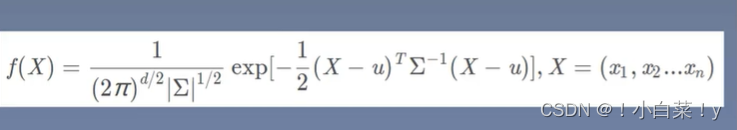
其中:
d 的值为确定的维度(n)
∑ 是斜方差(nxn的矩阵)
μ 是均值(n维向量)
-
-
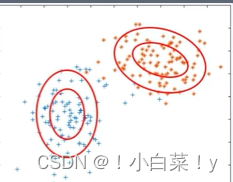
图像
- 一维特征
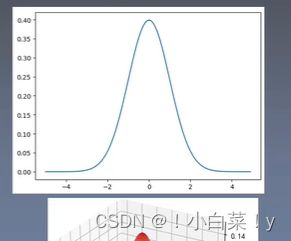
- 多维特征
- 一维特征
一、如何估计参数
-
我们所需的参数:
- Π
- μ
- σ
- 计算公式:
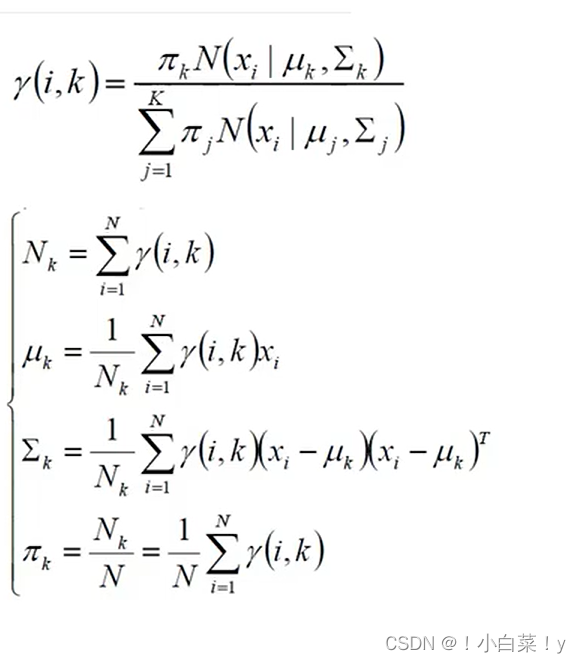
-
计算过程:
- 例子:已知一部分身高 求这一部分身高的男女分布
| x1 | x 2 | x 3 | x 4 |
|---|---|---|---|
| 1.58 | 1.78 | 1.62 | 1.81 |
-
- 假设
| 男 | μ1 = 1.71 | σ1 = 0.31 | Π1 = 0.5 |
|---|---|---|---|
| 女 | μ2= 1.62 | σ2 = 0.26 | Π2 = 0.5 |
-
- 求(相当于归一化)
- r(1,1) =Π1xN(x1|μ1,σ1) / (Π1xN(x1|μ1,σ1) +Π2xN(x1|μ2,σ2) )
- 其中:N(x1|μ1,σ1) 将数据带入高斯模型公式
- 依次求得 r(2,1) , r(3,1) , r(4,1) , r(1,2) , r(1,3) ,r(1,4)
- 求N
- N1=∑r(i,1) N2=∑r(i,2)
- 求新的Π
- Π1 = N1/N(N = 样本个数) Π2 =N2/N
- 求新的μ
- μ1= 1/N1 x (∑r(i,1) x xi)
- μ2= 1/N2 x (∑r(i,2) x xi)
- 求新的σ
- σ1 = 1/N1 x (∑r(i,1) x (xi-μ1)^2)
- σ2 = 1/N2 x (∑r(i,2) x (xi-μ2)^2)
- 其中: 平方那里如果是多维 就是改为乘以矩阵转置
- 更新之前的所有权重,迭代到一定次数最后达到收敛
二、二分类原生代码实现
import numpy as np
#随机种子
np.random.seed(0)
#假设男生的身高均值是1.71 标准差为 0.056
man_mean = 1.71
man_sigma = 0.056
#数据个数
num =10000
#男生数据
rand_data_man = np.random.normal(man_mean,man_sigma,num)
#标签 设男生的标签为1
y_man = np.ones(num)
#女生的身高均值1.58 标准差 0.051
np.random.seed(0)
women_mean = 1.58
women_sigma = 0.051
rand_data_women = np.random.normal(women_mean,women_sigma,num)
y_women = np.zeros(num)
#将数据混合
data = np.append(rand_data_man,rand_data_women)
data = data.reshape(-1,1)
# print(data)
y = np.append(y_man,y_women)
# print(y)
#聚类 用于两个类别
from scipy.stats import multivariate_normal
#迭代次数
num_iter = 1000
n,d = data.shape #n多少个数据 d维度
# print(n,d)
#初始化参数
mu1 = data.min(axis=0) #取最小的值 axis=0返回每列最小值
mu2 = data.max(axis=0)
sigma1 = np.identity(d) #identity创建方阵
sigma2 = np.identity(d)
# print(sigma2)
pai = 0.5
for i in range(num_iter):
#计算r --gamma
#计算N(x|mu,sigma)
norm1 = multivariate_normal(mu1,sigma1)
norm2 = multivariate_normal(mu2,sigma2)
tau1 = pai*norm1.pdf(data)
tau2 = (1-pai)*norm2.pdf(data)
r1 = tau1/(tau2+tau1)
r2 = 1-r1
#计算新的mu
mu1 = np.dot(r1, data) / np.sum(r1)
mu2 = np.dot(r2, data) / np.sum(r2)
#计算新的sigma
sigma1 = np.dot(r1 * (data - mu1).T, data - mu1) / np.sum(r1)
sigma2 = np.dot(r2 * (data - mu2).T, data - mu2) / np.sum(r2)
#pai
pai = np.sum(r1)/n
print('均值',mu1,mu2)
print('方差',sigma1,sigma2)
print(pai)
三、sklearn实现模型
#数据
# 随机种子
np.random.seed(0)
# 假设男生的身高均值是1.71 标准差为 0.056
man_mean = 1.71
man_sigma = 0.056
# 数据个数
num = 10000
# 男生数据
rand_data_man = np.random.normal(man_mean, man_sigma, num)
# 标签 设男生的标签为1
y_man = np.ones(num)
# 女生的身高均值1.58 标准差 0.051
np.random.seed(0)
women_mean = 1.58
women_sigma = 0.051
rand_data_women = np.random.normal(women_mean, women_sigma, num)
y_women = np.zeros(num)
# 将数据混合
data = np.append(rand_data_man, rand_data_women)
data = data.reshape(-1, 1)
# print(data)
y = np.append(y_man, y_women)
# print(y)
#模型
from sklearn.mixture import GaussianMixture
#n_components 有多少种类 max_iter迭代多少次
model = GaussianMixture(n_components=2,max_iter=1000)
model.fit(data)
print('pai:',model.weights_[0])
print('mean:',model.means_)
print('方差:',model.covariances_)
#预测
from sklearn.metrics import accuracy_score
y_pred = model.predict(data)
print(accuracy_score(y,y_pred))





![[附源码]java毕业设计校园闲置物品交易](https://img-blog.csdnimg.cn/8ed8c15106b443578755db2db1d59dde.png)