颜色模型

1.1 什么是RGB颜色模型

不知道你有没有近距离看过各种电子显示屏。若非常近距离的观察电子显示屏，可以发现屏幕居然是由

一个一个的红色、绿色、蓝色的小点组成。

红色的字母R(Red)，为一系列红色的点组成。
绿色的字母G(Green)，为一系列绿色的点组成。
蓝色的字母B(Blue)，为一系列蓝色的点组成。

rgb

用 RGB(红色的份数，绿色的份数，蓝色的份数) 。

例如

134份红色 + 172份绿色 + 242份蓝色 = 天空蓝，

RGB(134, 172, 242)

使用十六进制份数表示色值时，常常在前面加一个#号

 RGB(134, 172, 242)，134为十六进制的86，172为十六进制的ac，242为十六进制的f2。色值可以
写成 #86acf2 。

把背景设置天蓝色

#include <stdio.h>
#include <easyx.h>
int main(void)
{
    initgraph(800, 600);
    // 设置背景颜色为RGB(134, 172, 242)
    setbkcolor(RGB(134, 172, 242));
    cleardevice();
    getchar();
    closegraph();
    return 0;
}

hsv

是一个色环 0 到120 红色到绿色过渡 120到240 是绿色到蓝色过渡

240到360 是蓝色到红色过渡

其次自每个角度下 存在着饱和度和亮度

饱和度就是这个色彩的鲜艳 0%为白色 不饱和 100%最饱和

亮度 就是色彩的明暗 0%位黑色最暗 100%最亮

hsv转换为rgb

因为电脑不支持hsv 所以需要把hsv 转为rgb

COLORREF HSVtoRGB(
    float H,//Hue(色相) 分量，0 <= H < 360
    float S,//Saturation(饱和度) 分量，0 <= S <= 1
    float V//Value(明度) 分量，0 <= V <= 1
);

// 设置背景颜色为HSV(219°, 45%, 95%)
setbkcolor(HSVtoRGB(219, 0.45, 0.95));

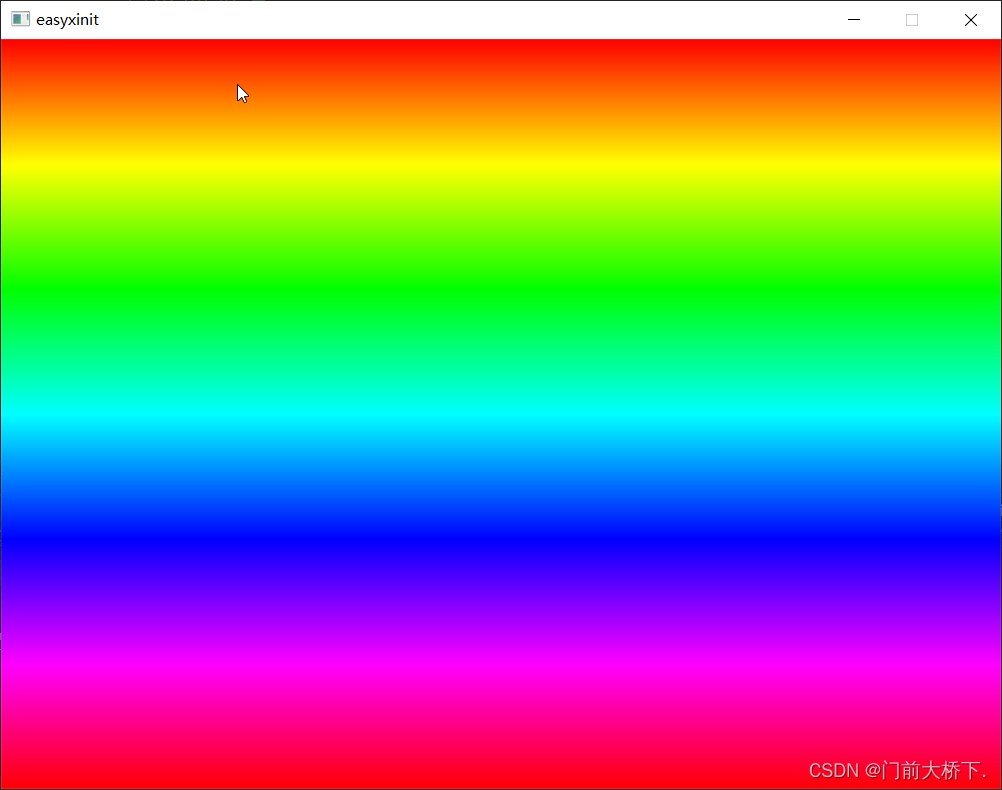
案例 绘制彩虹窗体

#include <easyx.h>
#include <stdio.h>
int main() {
	//创建画布
	initgraph(800, 600);
	
	//把画布分成600份  每份就是一个线条 线条的颜色根据hsv的角度变换
	//,每次变动的角度
	float delt = 360.0 / 600.0;
	float h=0;
	//600个线条
	for (int i = 0; i < 600; i++)
	{
		//设置颜色
		setlinecolor(HSVtoRGB(h, 1, 1));

		//在画布上绘制线条
		line(0,i,800,i);
		//变换角度
		h += delt;
	}

	//关闭前拦截一下 
	getchar();
	//关闭画布
	closegraph();
	return 0;
}

方案二

#include <easyx.h>
#include <stdio.h>
int main() {
	//创建画布
	initgraph(800, 600);
	
	//把画布分成600份  每份就是一个线条 线条的颜色根据hsv的角度变换

	//600个线条
	for (int i = 0; i < 600; i++)
	{
		//,每次变动的角度
		float delt = 360.0 / 600.0;

		//设置颜色
		setlinecolor(HSVtoRGB(i * delt, 1, 1));

		//在画布上绘制线条
		line(0,i,800,i);
	}

	//关闭前拦截一下 
	getchar();
	//关闭画布
	closegraph();
	return 0;
}

案例 绘制天空和彩虹画面

#include <easyx.h>
#include <stdio.h>

int main() {
	//创建画布
	initgraph(800, 600);
	
	//把画布分成600份  每份就是一个线条 线条的颜色根据hsv的角度变换

	//600个线条
	for (int i = 0; i < 600; i++)
	{
		//,每次变动的饱和度
		float delt = 1.0 / 600.0;

		//设置颜色
		setlinecolor(HSVtoRGB(240, 1- i * delt, 1));

		//在画布上绘制线条
		line(0,i,800,i);

	}

	//绘制彩虹
	//获得圆心
	//变换的色彩度数
	float ch = 360.0 / 100.0;
	for (int i = 0; i < 100; i++)
	{
		//绘制线条样式
		setlinecolor(HSVtoRGB(ch*i,1,1));
		circle(400, 600, 300-i);
	}

	//关闭前拦截一下 
	getchar();
	//关闭画布
	closegraph();
	return 0;
}