目录
1.定义和影响
1.1自相关性产生的原因
1.2自相关的后果
2.减小影响方法
2.1如何判断数据存在自相关性
a.用相关计量软件
b.Durbin-Watson Statistics(德宾-瓦特逊检验)
c.Q-Statistics 以(box-pierce)- Eviews(7th version第七版本)为例子
2.2如何减弱模型的自相关性
a.GLS or FGLS
b.HAC:Heteroscedasticity Autocorrelation consistent
自相关性是指随机误差项的各期望值之间存在着相关关系,称随机误差项之间存在自相关性(autocorrelation)或序列相关,于1972年提出。
1.定义和影响
对于模型:
如果随机误差项的各期望值之间存在着相关关系,即:
这时,称随机误差项之间存在自相关性(autocorrelation)或序列相关。
随机误差项的自相关性可以有多种形式,其中最常见的类型是随机误差项之间存在一阶自相关性或一阶自回归形式,即随机误差项只与它的前一期值相关: 或者
,则称这种关系为一阶自相关。
p阶自相关性可以表示为:
是满足回归模型基本要求的随机误差项。我们称之为p 阶自回归形式,或模型存在 p 阶自相关。
由于无法观察到误差项,只能通过残差项
来判断
的行为。如果
或
呈现出图1(a)-(d)形式,则表示
存在自相关,如果
或
呈现图1中(e)形式,则表示
不存在自相关。
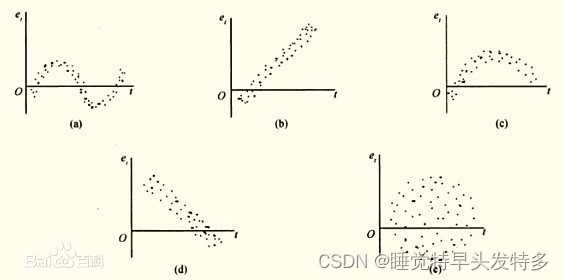
线性回归模型中的随机误差项的序列相关问题较为普遍,特别是在应用时间序列资料时,随机误差项的序列相关经常发生。
1.1自相关性产生的原因
线性回归模型中随机误差项存在序列相关的原因很多,但主要是经济变量自身特点、数据特点、变量选择及模型函数形式选择引起的。
1.经济变量惯性的作用引起随机误差项自相关;
2.经济行为的滞后性引起随机误差项自相关;
3.一些随机因素的干扰或影响引起随机误差项自相关;
4.模型设定误差引起随机误差项自相关;
5.观测数据处理引起随机误差项序列相关。
1.2自相关的后果
线性相关模型的随机误差项存在自相关的情况下,用OLS(普通最小二乘法)进行参数估计,会造成以下几个方面的影响。
从高斯——马尔可夫定理的证明过程中可以看出,只有在同方差和非自相关性的条件下,OLS估计才具有最小方差性。当模型存在自相关性时,OLS估计仍然是无偏估计,但不再具有有效性。这与存在异方差性时的情况一样,说明存在其他的参数估计方法,其估计误差小于OLS估计的误差;也就是说,对于存在自相关性的模型,应该改用其他方法估计模型中的参数。
1.自相关不影响OLS估计量的线性和无偏性,但使之失去有效性;
2.自相关的系数估计量将有相当大的方差;
3.自相关系数的T检验不显著;
4.模型的预测功能失效。
2.减小影响方法
2.1如何判断数据存在自相关性
a.用相关计量软件
比如说E-VIEWS检查残差的分布。 如果残差分布具有明显和圆润的线性分布图像, 说明自相关性存在的可能性很高。反之, 无规则波动大的分布图像显示出相关性微弱。比如,以下图片,左边较为圆润的分布就显示出自相关性的存在,右边波动大的则反之。
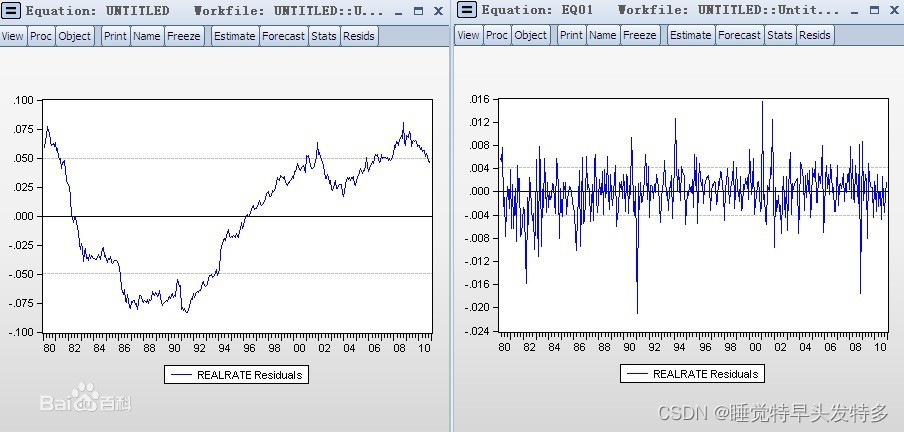
b.Durbin-Watson Statistics(德宾-瓦特逊检验)
假设time series模型存在自相关性,我们假设误差项可以表述为 Ut=ρ*Ut-1+ε. 利用统计检测设立假设,如果ρ=o.则表明没有自相关性。Durbin-Watson统计量(后面简称DW统计量)可以成为判断正、负、零(无)相关性的工具。 DW统计量: d=∑(Ut-Ut-1)^2/∑ut^2≈2*(1-ρ).如果d=2则基本没有自相关关系,d靠近0存在正的相关关系,d靠近4则有负的相关关系。
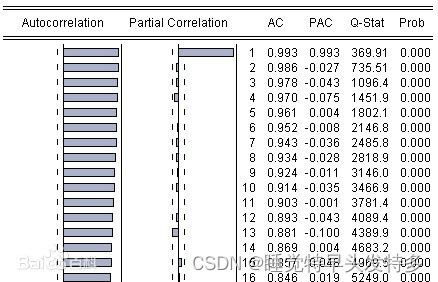
c.Q-Statistics 以(box-pierce)- Eviews(7th version第七版本)为例子
很多统计计量软件软件提供Q test来检测,这里用Eviews为例子。 Q的统计量(test statistics)为 Q=n*∑ρ^2. 零假设null hypothesis H0=0和方法2的含义一样。如果零假设证明失败,则对立假设ρ≠0成立,意味着有自相关性。下图中的Q-test就显示出相关性。
2.2如何减弱模型的自相关性
a.GLS or FGLS
假设存在自相关性的模型,误差项之间的关系为:Ut=ρ*Ut-i+ε(ε为除了自相关性的误差项),i.i.d~(0,σ). t时期的模型为 yt=βxt+Ut, t-1时期则为 ρ*yt-1=ρ*βxt-1+ρ*Ut-1。用t时期的减去t-1时期的可得出yt-yt-1=β(xt-xt-1)+(Ut-Ut-1).已知 Ut-Ut-1=ε。经过整理后新的模型满足Gauss-Makov的假设和,White noise condition(同方差性或者等分散),没有自相关性。
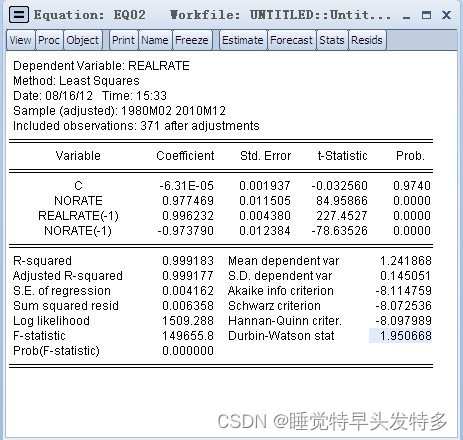
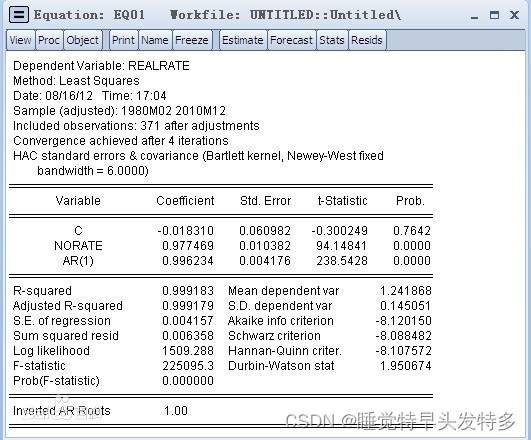
b.HAC:Heteroscedasticity Autocorrelation consistent
以Eviews为例子,在分析模型时选择HAC,在模型中逐渐添加time lag的数目,来校正DW统计量达到正常值减少自相关性。
自相关性_百度百科