矩阵分析:特征值分解
- 前置知识
- 空间变换
- 伸缩
- 旋转
- 对称矩阵
- 对称矩阵对角化
- 正交矩阵
- 向量的基
- 基变换
- 不同基下的向量变换
- 逆矩阵
- 不同基下的空间变换
- 内积的几何意义
- 特征值、特征向量
- 特征值分解
- 代码
前置知识
空间变换
伸缩
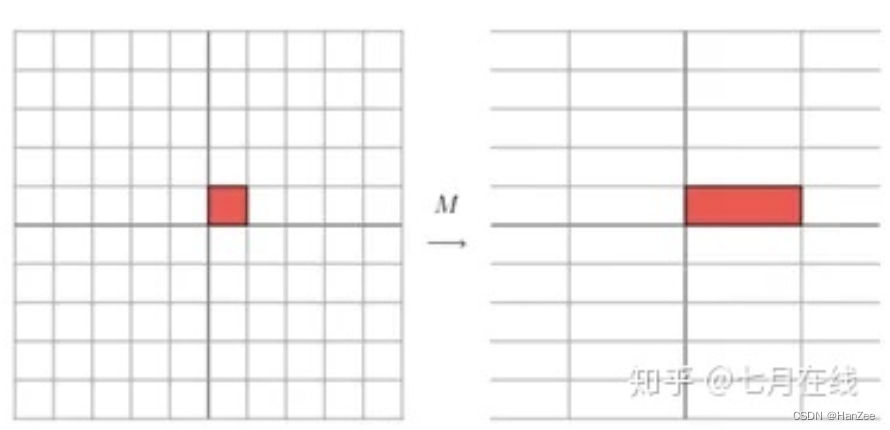
一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵:
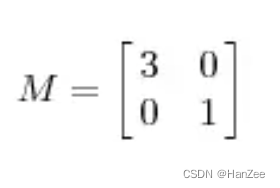
因为这个矩阵M乘以一个向量(x,y)的结果是:

旋转
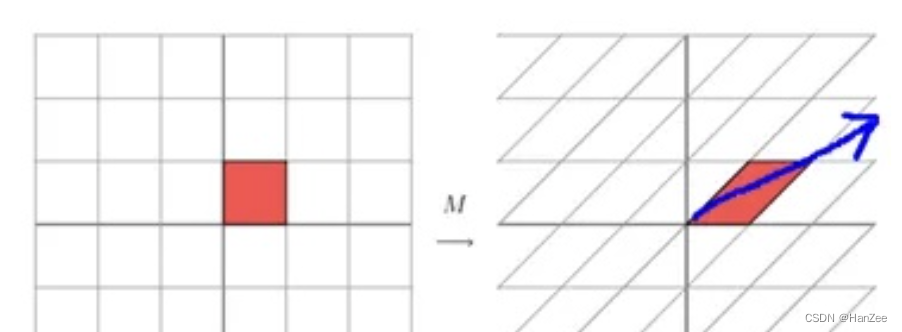
除了伸缩变换,也可以进行旋转变换。
上面的矩阵是对称的,所以这个变换是一个对x,y轴的方向一个拉伸变换(每一个对角线上的元素将会对一个维度进行拉伸变换,当值>1时,是拉长,当值<1时时缩短),当矩阵不是对称的时候,假如说矩阵是下面的样子:
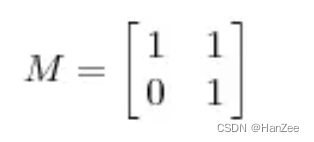
对称矩阵
对称矩阵(Symmetric Matrix)是指元素以主对角线为对称轴对应相等的矩阵,例如:
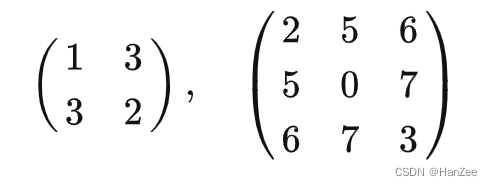
他的转置等于它本身。
对称矩阵对角化
如果一个对称矩阵是实对称矩阵,就会存在正交矩阵P,与对角矩阵满足下列等式:
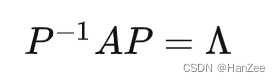
然后我们对等式两边左乘P,右乘P的逆矩阵,就会得到:
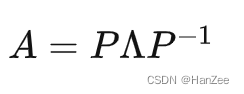
又因为正交矩阵的转置=它的逆矩阵,所以对称矩阵的对角化如下:

正交矩阵

- 正交矩阵的每一个行向量与其他行向量相互垂直(内积=0),每一个列向量与其他列向量相互垂直。
- 行向量或者列向量他与本身的内积=1,也就是长度=1(单位向量)。
- 正交矩阵的逆矩阵=它的转置矩阵
向量的基
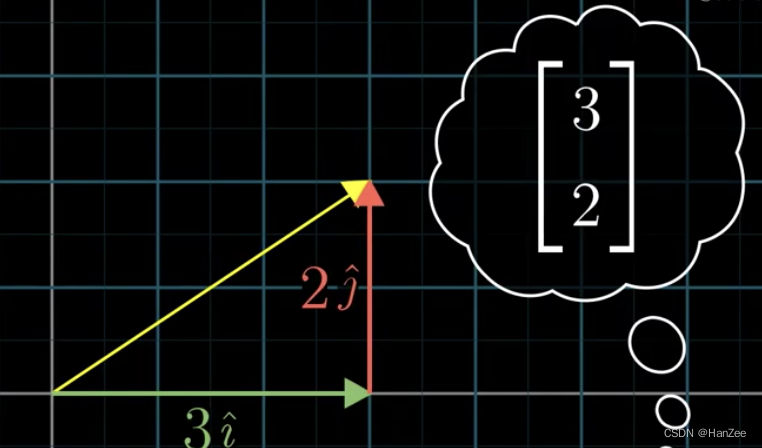
假设有一个列向量A:=[3,2],如下图:

我们假设图中每个蓝色方格的单位为1,那么即使图中没有标注黄色向量是谁,我们也可以脱口而出他就是[3,2]。那么为什么我们可以直接看出他是谁呢?
答案也很简单,因为我们根据有一个参考依据,那就是坐标系(笛卡尔坐标系)。然而,这个二维坐标系他其实是由两个基向量:i ,j所组成的空间,其中:
i
=
[
1
,
0
]
T
,
j
=
[
0
,
1
]
T
i=[1,0]^T ,j=[0,1]^T
i=[1,0]T,j=[0,1]T
我们可以把A看成在i向量扩大三倍,j扩大2倍,然后让他们作向量加法:
A → = 3 ⋅ i → + 2 j → = 3 [ 1 0 ] + 2 [ 0 1 ] = [ 1 0 0 1 ] [ 3 2 ] = [ 3 2 ] \begin{aligned}\overrightarrow{A}=3\cdot \overrightarrow{i}+2\overrightarrow{j}=3\begin{bmatrix} 1 \\ 0 \end{bmatrix}+2\begin{bmatrix} 0 \\ 1 \end{bmatrix}\\ =\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} 3 \\ 2 \end{bmatrix}\\ =\begin{bmatrix} 3 \\ 2 \end{bmatrix}\end{aligned} A=3⋅i+2j=3[10]+2[01]=[1001][32]=[32]
基变换
假设有两个人,小泽,小乐,他们看待问题的‘角度’不认同,也、也就是基不同,其中小泽的基向量为:
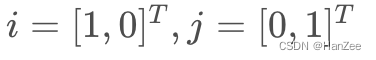
而小乐的基向量为为:b1 ,b2,b1b2这两个向量在小乐看来数值就是
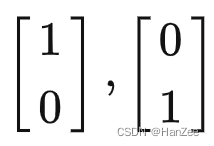
然而在小泽看来b1,b2数值为:
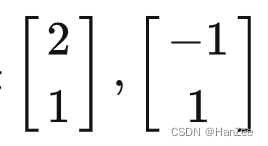
上面的向量A,在小泽的角度来看,就是[3,2],然而在小乐的角度看就变成了:[5/3,1/3]。

它们之所以认为这个向量是不同的,因为它们看待问题的角度不同,‘横看成岭侧成峰,远近高低各不同’,也就是基向量不同。
不同基下的向量变换
假设小泽角度下的向量B:
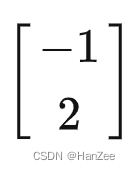
现在我们知道小泽与小乐的基向量,还知道了向量B在小泽中的数值表示,那么我们如果把小泽角度看的向量B,用小乐的角度表示,计算公式应该为:
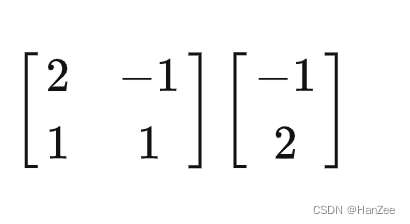
于是,我们就把小泽角度下的向量B,转换成了小乐角度的向量。
逆矩阵
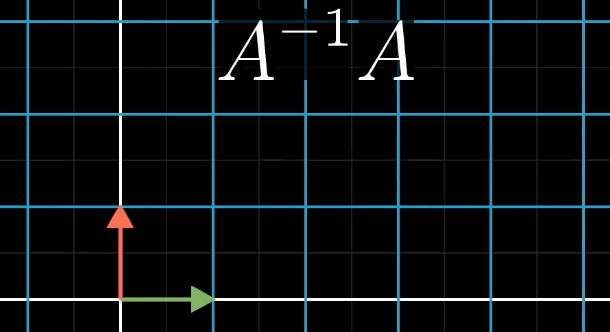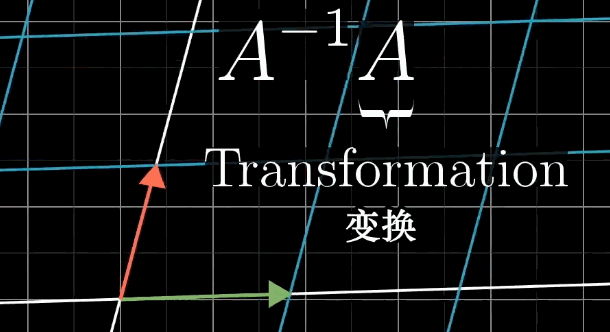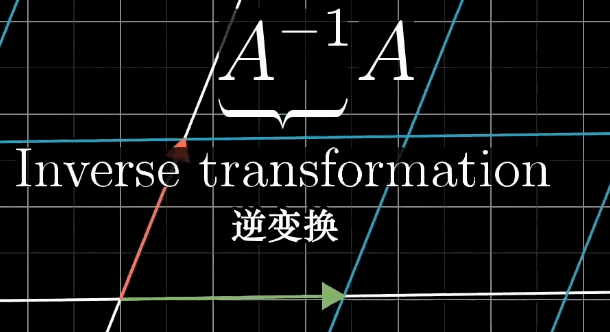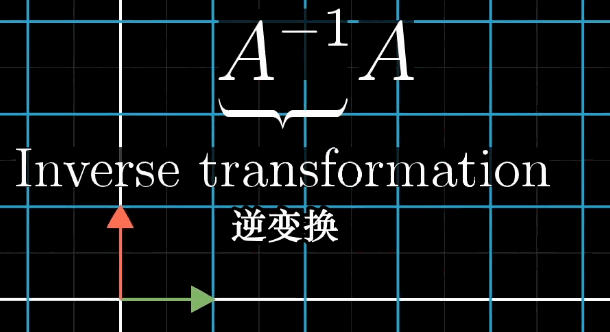
A的逆矩阵代表的含义就是A变换的逆过程。
求解 Ax =b的几何意义,就是找到一个向量x使得在A的变换下,x被映射为b。如果A为满秩矩阵,则有唯一解
x
=
A
−
1
b
x=A^{-1}b
x=A−1b ,也就是对b施加逆变换即可找到x。
在上面我们说在小泽的眼中,小乐的基向量b1,b2就是:
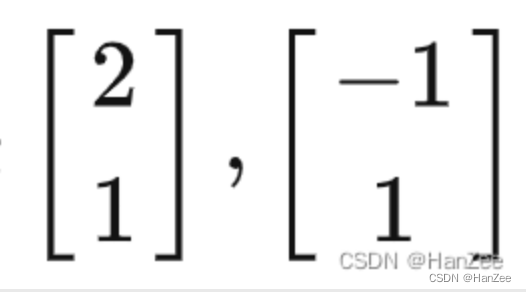
那么在小乐的眼中(以b1,b2为基向量),小泽的基向量i,j 如何表示呢?
这时候就用到了逆矩阵,把小泽的视角下的小乐的基向量的表示切换到小乐的视角小泽基向量的表示,需要用到上图矩阵做变换,那么我们反过来,就得到:

不同基下的空间变换
在上面我们已经介绍了什么是不同基下如何转换向量,下面我们介绍我们在不同基下的空间变换。
在小泽的视角中,我们如果想把坐标系逆时针旋转90度,如下图:
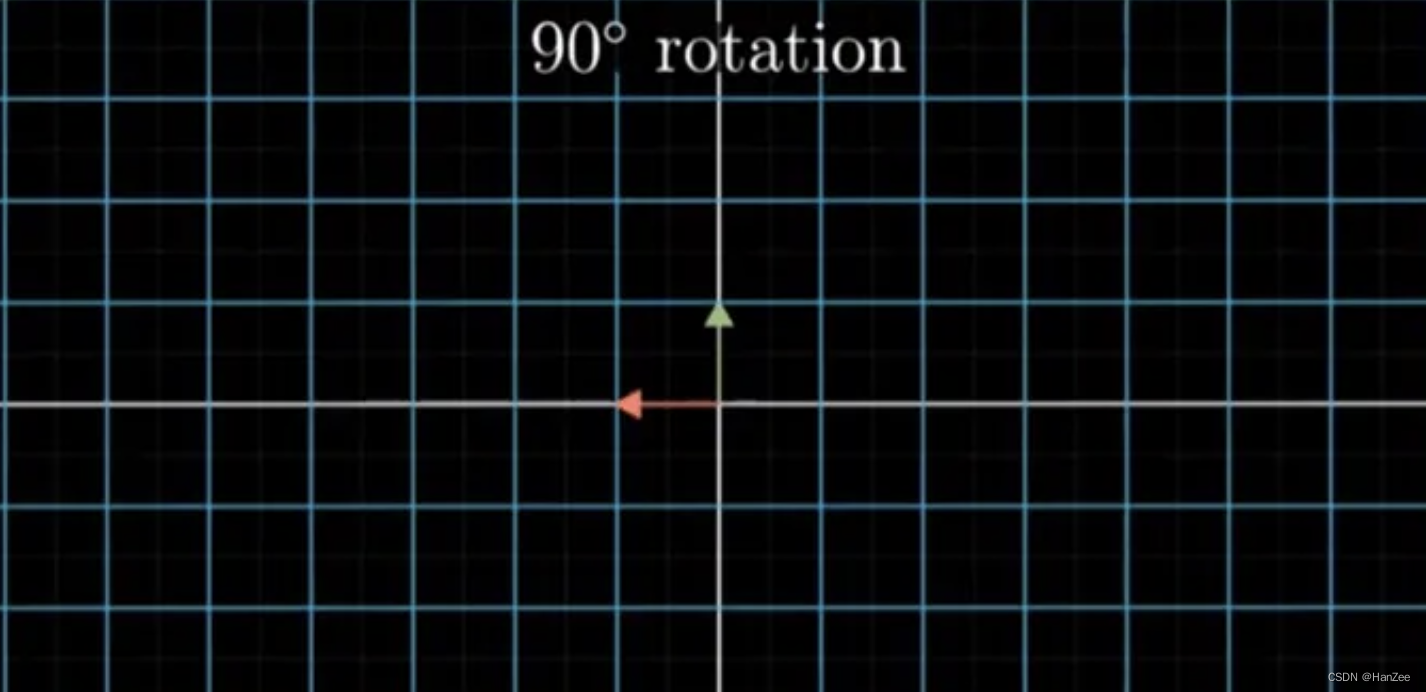
这个变换在小泽的视角下用矩阵A表示则是:
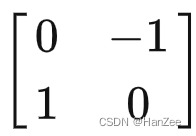
那么我们想做的就是知道:在小乐的视角下这个变换矩阵怎么表示呢?
现在我们已经有的是:二者的基向量,小泽的旋转矩阵。
我们的流程是:
- 在小乐的视角下找到一组向量
- 把这组向量用小泽的视角表示
- 然后把这向量通过旋转矩阵得到旋转后的向量
- 把旋转后的向量通过逆矩阵返回到小乐的视角
其中P为小乐视角下小泽基向量的表示,A为旋转矩阵,P的逆矩阵是小泽视角下小乐基向量的表示。
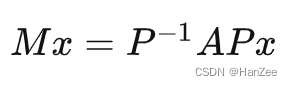
其中M就是我们要的小乐视角下的旋转矩阵,这就表示了不同基向量下的相同变换的相互转化。
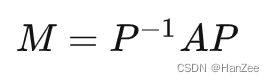
内积的几何意义
向量与基向量的内积,就是向量在基向量方向上的投影坐标。
点乘(Dot Product)的结果是点积,又称数量积或标量积(Scalar Product)。在空间中有两个向量:
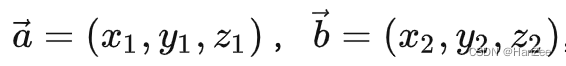
从代数角度看,点积是对两个向量对应位置上的值相乘再相加的操作,其结果即为点积。
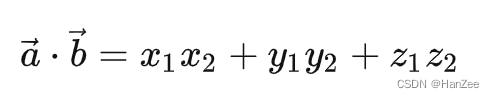
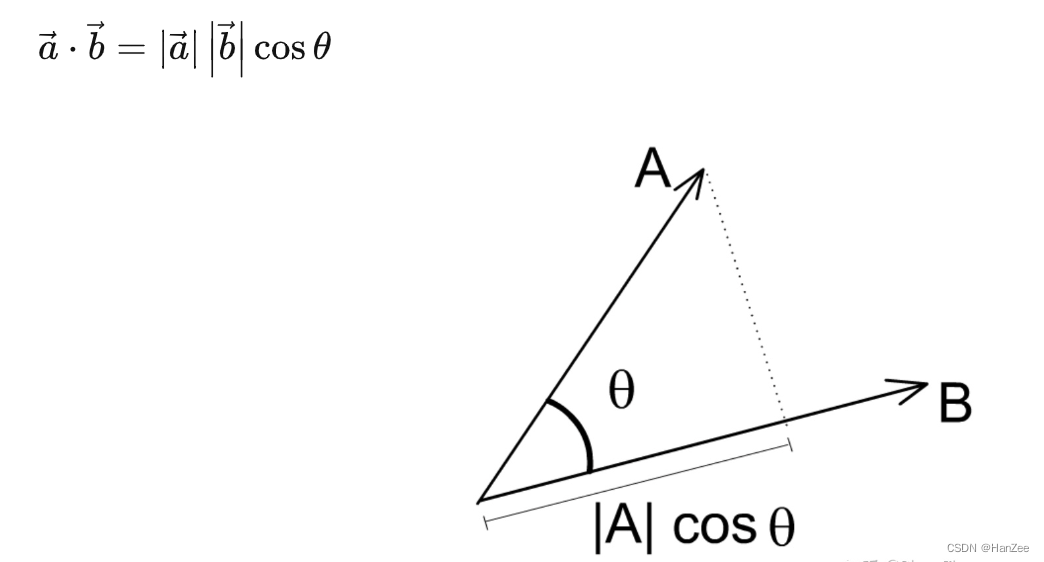
从几何角度看,点积是两个向量的长度与它们夹角余弦的积。
特征值、特征向量

向量x1,x2在矩阵A的作用下进行了空间变换,x1–>Ax1 , x2–> Ax2
其中Ax2与x2的方向一直,说明矩阵A只对x2起到了伸缩作用,我们把Ax2写成大小与方向的表达式,
λ
x
2
\lambda x_2
λx2:
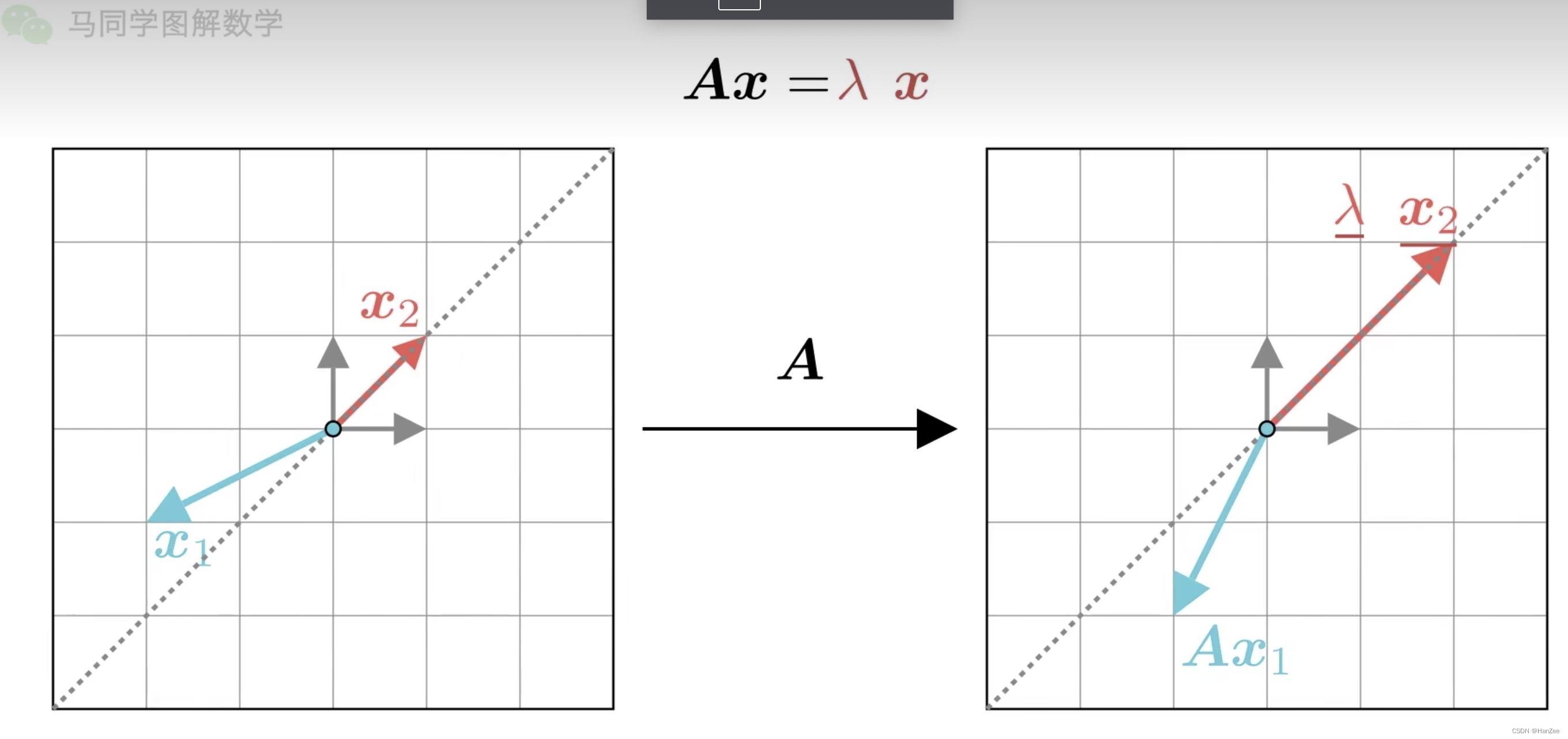
于是我们就是:lambda 为变换矩阵A的特征值,x2为变换矩阵A lambda这个特征值对应的特征向量。
特征值分解
特征值分解可以得到特征值与特征向量,特征值表示的是这个特征到底有多重要,而特征向量表示这个特征的方向。
如果说一个向量v是一个方阵A的特征向量,将一可以表示成下面形式
A
v
=
λ
v
Av=\lambda v
Av=λv
λ
\lambda
λ为特征向量v的特征值,特征值分解是将一个矩阵分解为如下形式:
A
=
Q
∑
Q
−
1
A=Q\sum Q^{-1}
A=Q∑Q−1
其中Q是这个矩阵A的特征向量所组成的矩阵,
∑
\sum
∑是一个对角矩阵,每一个对角线元素就是一个特征值,里面的特征值有大到小排列,这些特征值所对应的特征向量就是描述这个矩阵变化方向,(从主要的变化到次要的变化排序)。也就是说矩阵A的信息可以由其特征值和特征向量表示。
对于矩阵为高纬的情况下,那么这个矩阵就是高维空间下的一个线性变换,可以想像,这个变化也同样有很多的变换方向,我们通过特征值分解得到的前N个特征向量,那就对应了这个矩阵最主要的N个变化方向,我们利用这前N个变化方向,就可以近似这个矩阵(变换)。
代码
import numpy as np
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
V, U = np.linalg.eig(A)
print(V)
print(U)
# 特征值分解的应用
1. PCA
2. SVD
3. 图像压缩
4. 控制系统