目录
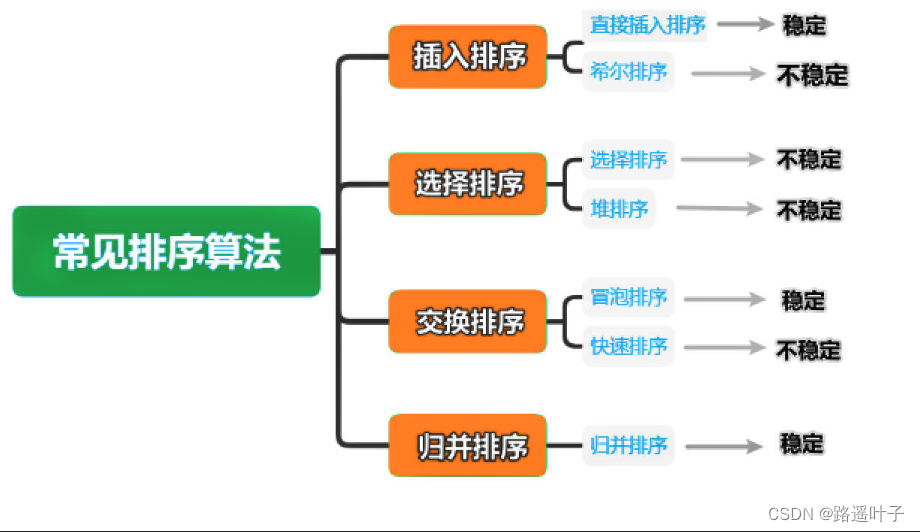
一、插入排序:直接插入排序【稳定排序方法】
二、插入排序:希尔排序【不稳定排序方法】
三、选择排序:直接选择排序【不稳定排序方法】
四、选择排序:堆排序【不稳定排序方法】
五、交换排序:冒泡排序【稳定排序方法】
六、交换排序:快速排序【不稳定排序方法】
七、归并排序:归并排序【稳定排序方法】
前言
排序是计算机程序设计中的一种重要操作,其功能是对一个数据元素集合或序列重新排列成一个按数据元素某个相知有序的序列。排序分为两类:内排序和外排序。
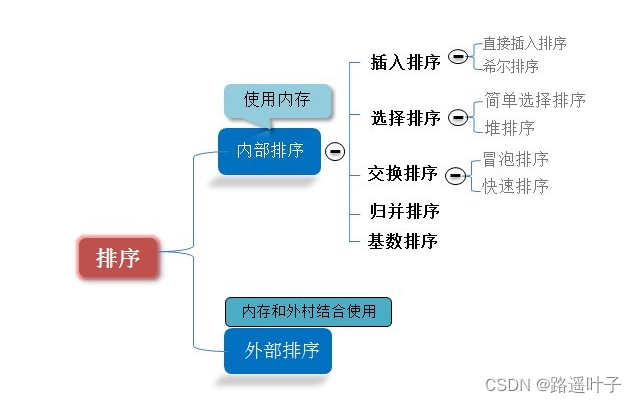
今天为大家总结一下,常见的七大排序:
一、插入排序:直接插入排序【稳定排序方法】
1.概述
1.1 插入排序,一般也被称为直接插入排序。
1.2 插入排序:每次将一个待排序的记录,按其关键字的大小插入到前面已排序好的记录序列中的适当位置,直到全部记录插入完成为止。
1.3 直接插入排序是一种最简单的排序方法,其基本操作是将一条记录插入到已排好的有序表中,从而得到一个新的、记录数量增1的有序表。

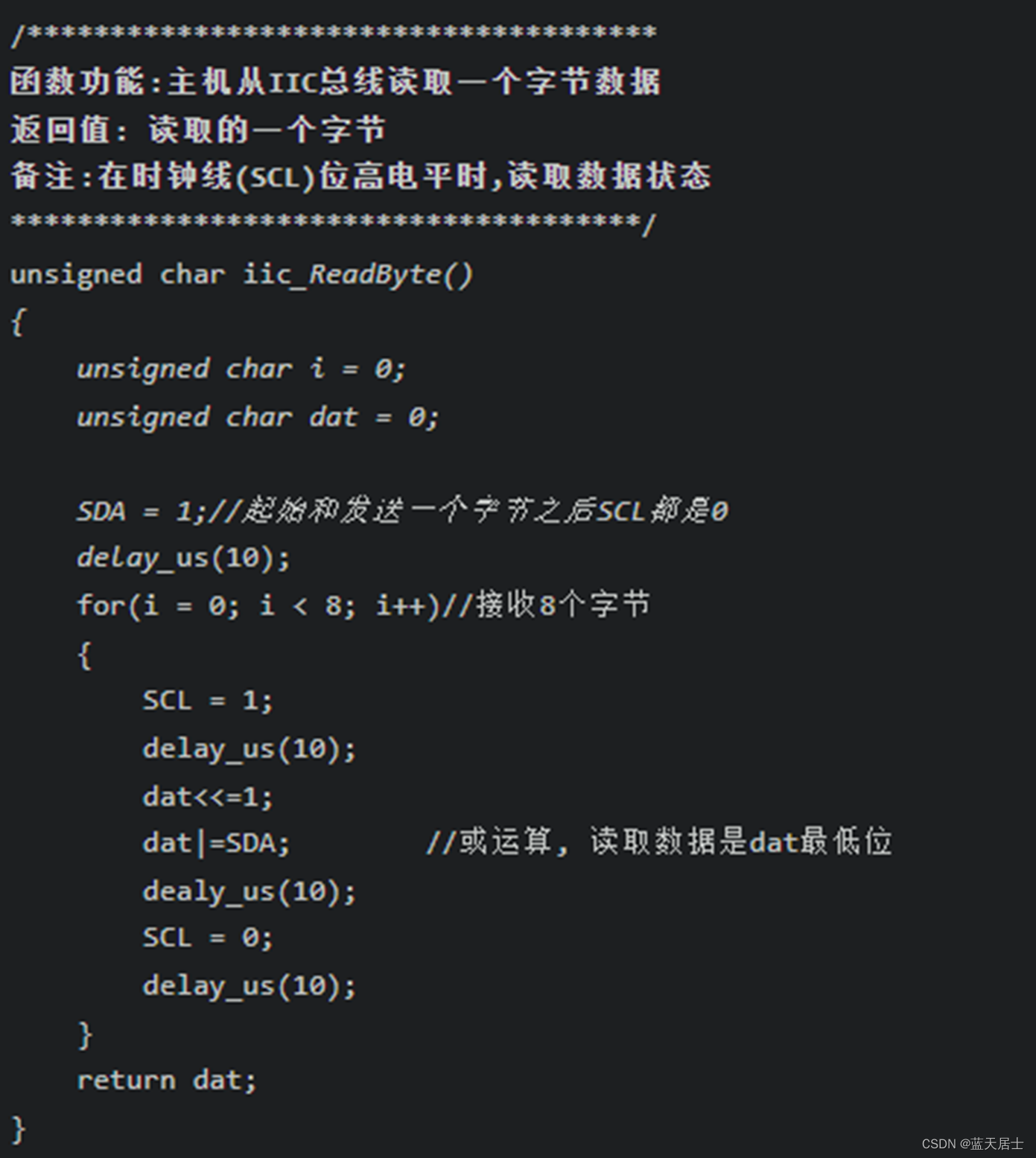
2. 算法实现:
2.1不带监视哨
//【算法1】 不带监视哨的直接插入排序算法
public void insertSort() {
RecordNode temp;
int i, j;
for (i = 1; i < this.curlen; i++) { // n-1趟扫描
temp = r[i]; // 将待插入的第i条记录暂存在temp中
for (j = i - 1; j >= 0 && temp.key.compareTo(r[j].key) < 0; j--) {
r[j + 1] = r[j]; // 将前面比r[i]大的记录向后移动
}
r[j + 1] = temp; // r[i]插入到第j+1个位置
//System.out.print("第" + i + "趟: ");
//display();
}
}2.2带监视哨
//【算法2】带监视哨的直接插入排序算法
public void insertSortWithGuard() {
int i, j;
// System.out.println("带监视哨的直接插入排序");
for (i = 1; i <this.curlen; i++) { //n-1趟扫描
r[0] = r[i]; //将待插入的第i条记录暂存在r[0]中,同时r[0]为监视哨
for (j = i - 1; r[0].key.compareTo(r[j].key) < 0; j--) { //将前面较大元素向后移动
r[j + 1] = r[j];
}
r[j + 1] = r[0]; // r[i]插入到第j+1个位置
System.out.print("第" + i + "趟: ");
display(9);
}
}二、插入排序:希尔排序【不稳定排序方法】
1.概述
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。
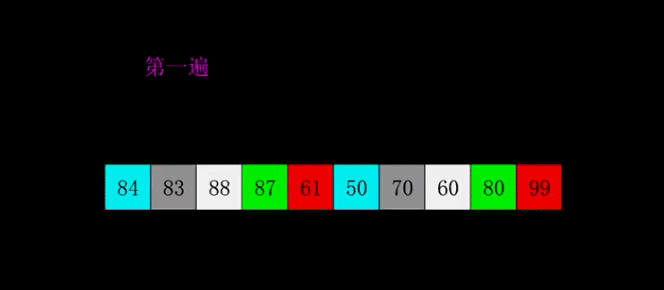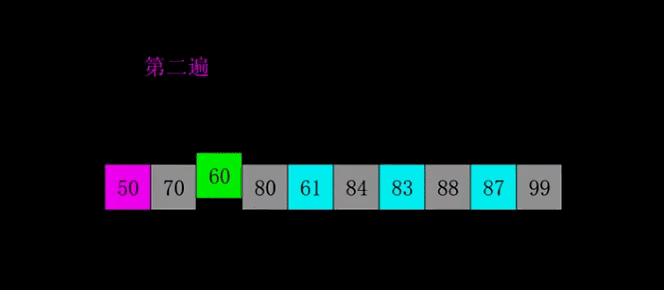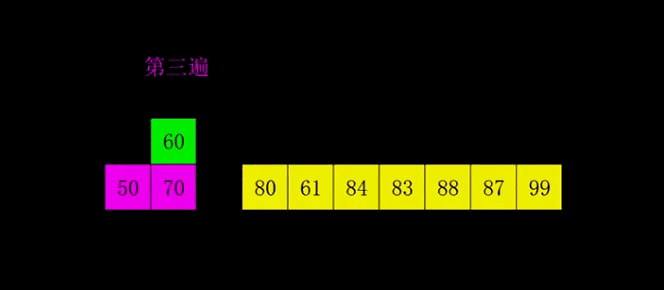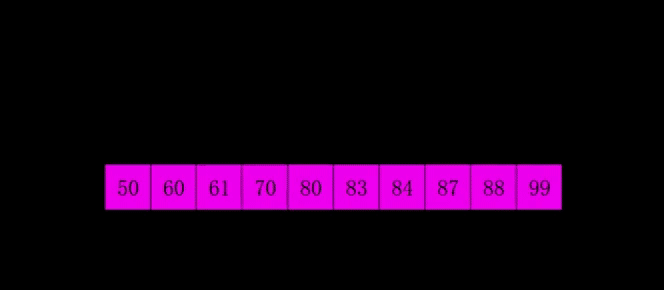
2. 算法实现
//【算法3】希尔排序算法
public void shellSort(int[] d) { //d[]为增量数组
RecordNode temp;
int i, j;
System.out.println("希尔排序");
//控制增量,增量减半,若干趟扫描
for (int k = 0; k < d.length; k++) {
//一趟中若干子表,每个记录在自己所属子表内进行直接插入排序
int dk = d[k];
for (i = dk; i < this.curlen; i++) {
temp = r[i];
for (j = i - dk; j >= 0 && temp.key.compareTo(r[j].key) < 0; j -= dk) {
r[j + dk] = r[j];
}
r[j + dk] = temp;
}
System.out.print("增量dk=" + dk + " ");
display();
}
}三、选择排序:直接选择排序【不稳定排序方法】
1.概述
-
首先在所有记录中选出关键字值最小的记录,把它与第一个记录进行位置交换,
-
然后在其余的记录中再选出关键字值次小的记录,与第二个记录进行位置交换。
-
依次类推,直到所有记录排好序。
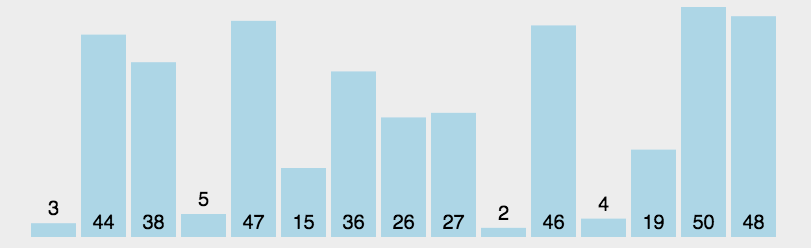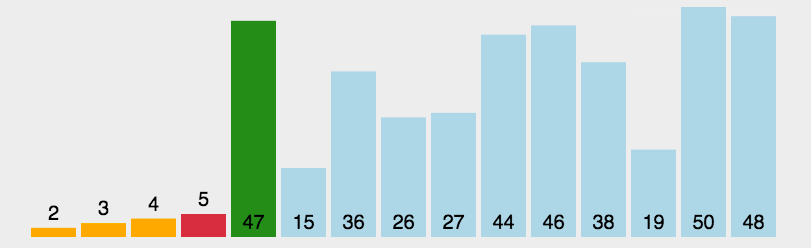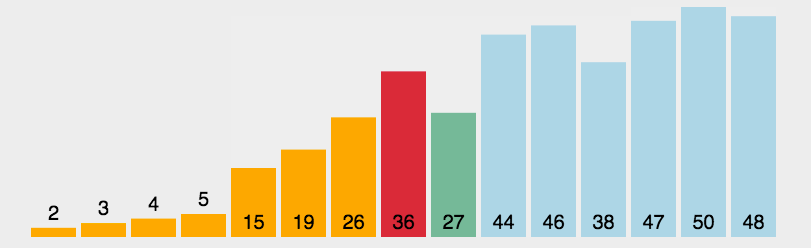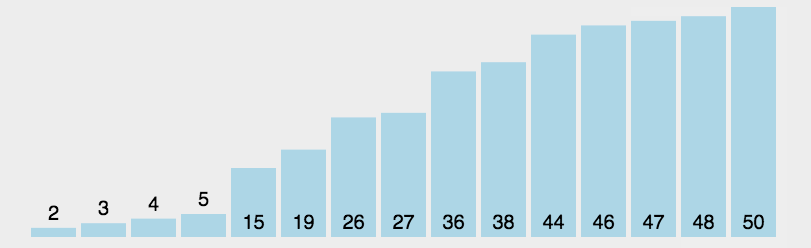
2. 算法实现
//【算法】直接选择排序
public void selectSort() {
// System.out.println("直接选择排序");
RecordNode temp; //辅助结点
for (int i = 0; i < this.curlen - 1; i++) {//n-1趟排序
//每趟在从r[i]开始的子序列中寻找最小元素
int min = i; //设第i条记录的关键字最小
for (int j = i + 1; j < this.curlen; j++) {//在子序列中选择关键字最小的记录
if (r[j].key.compareTo(r[min].key) < 0) {
min = j; //记住关键字最小记录的下标
}
}
if (min != i) { //将本趟关键字最小的记录与第i条记录交换
temp = r[i];
r[i] = r[min];
r[min] = temp;
}
System.out.print("第" + (i + 1) + "趟: ");
display();
}
}四、选择排序:堆排序【不稳定排序方法】
1.概述
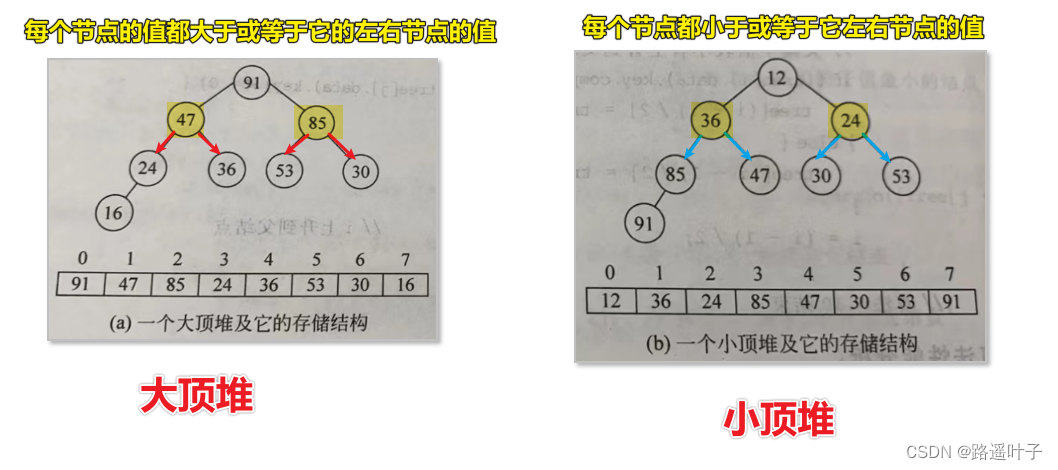
堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
-
大顶堆:每个节点的值都大于或者等于它的左右子节点的值。
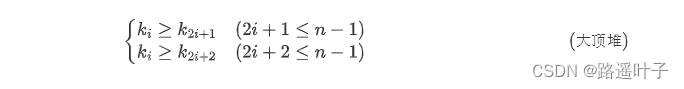
-
小顶堆:每个节点的值都小于或者等于它的左右子节点的值。
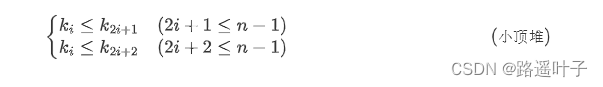
-
一般升序采用大顶堆,降序采用小顶堆
2.示意图
3.算法实现
基本思想:
1. 首先将这n条记录按关键字值的大小建立堆(称为初始堆),将堆顶元素r[0]与r[n-1]交换
2. 然后,将剩下的{r[0]..r[n-2]}序列调整成堆
3. 再将 r[0]与r[n-2]交换,再将剩下的{r[0]..r[n-3]}序列调整成堆
4. 如此反复,直到整个序列有序。
5. 这个过程称为堆排序
3.1 筛选法调整堆:算法
//【算法】将以筛选法调整堆算法
//将以low为根的子树调整成小顶堆,low、high是序列下界和上界
public void sift(int low, int high) {
int i = low; //子树的根
int j = 2 * i + 1; //j为i结点的左孩子
RecordNode temp = r[i];
while (j < high) { //沿较小值孩子结点向下筛选
if (j < high - 1 && r[j].key.compareTo(r[j + 1].key) > 0) {
j++; //数组元素比较,j为左右孩子的较小者
}
if (temp.key.compareTo(r[j].key) > 0) { //若父母结点值较大
r[i] = r[j]; //孩子结点中的较小值上移
i = j;
j = 2 * i + 1;
} else {
j = high + 1; //退出循环
}
}
r[i] = temp; //当前子树的原根值调整后的位置
// System.out.print("sift " + low + ".." + high + " ");
// display();
}3.2堆排序:算法
//【算法】 堆排序算法
public void heapSort() {
// System.out.println("堆排序");
int n = this.curlen;
RecordNode temp;
// 从最后一个非叶子节点开始调整堆,直到根结点
for (int i = n / 2 - 1; i >= 0; i--) {//创建堆
sift(i, n);
}
System.out.println("堆构建完成");
for (int i = n - 1; i > 0; i--) {//每趟将最小值交换到后面,再调整成堆
// 第一个元素和无序中的最后一个交换
temp = r[0];
r[0] = r[i];
r[i] = temp;
sift(0, i);
}
}五、交换排序:冒泡排序【稳定排序方法】
1.概述
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
将待排序的数组看成从上到下的存放,把关键字较小的记录看成较轻的,关键字较大的记录看成较重的。
较小关键字值的记录,好像水中的气泡一样,向上浮;
较大关键字值的记录,好像水中的石块一样,向下沉;
当所有的气泡都浮到了相应的位置,并且所有的石块都沉到了水中,排序就结束了
2.算法实现
//【算法】 冒泡排序算法
public void bubbleSort() {
// System.out.println("冒泡排序");
RecordNode temp; // 辅助结点
boolean flag = true; // 是否交换的标记
for (int i = 1; i < this.curlen && flag; i++) { // 有交换时再进行下一趟,最多n-1趟
flag = false; // 假定元素未交换
for (int j = 0; j < this.curlen - i; j++) { // 一次比较、交换
if (r[j].key.compareTo(r[j + 1].key) > 0) { // 逆序时,交换
temp = r[j];
r[j] = r[j + 1];
r[j + 1] = temp;
flag = true; //如果发生交换,记录
}
}
System.out.print("第" + i + "趟: ");
display();
}
}六、交换排序:快速排序【不稳定排序方法】
1.概述
快速排序:Quick Sort
通过一趟排序将要排序的记录分割成独立的两个部分,其中一部分的所有记录的关键字值都比另外一部分的所有记录关键字值小。
然后再按此方法对这两部分记录分别进行快速排序。
整个排序过程可以递归进行,以此达到整个记录序列变成有序

2.算法实现
2.1一趟快速排序
//【算法】一趟快速排序
//交换排序表r[i..j]的记录,使支点记录到位,并返回其所在位置
//此时,在支点之前(后)的记录关键字均不大于(小于)它
public int Partition(int i, int j) {
RecordNode pivot = r[i]; //第一个记录作为支点记录
System.out.println(i + ".." + j + ", pivot=" + pivot.key + " ");
System.out.print("初始值: ");
int c = 0;
display();
while (i < j) { //从表的两端交替地向中间扫描
// 1.1 从后到前,寻找第一个比支点小的元素
while (i < j && pivot.key.compareTo(r[j].key) <= 0) {
j--;
}
// 1.2 将后面较小的元素,移到前面去
if (i < j) {
r[i] = r[j]; //将比支点记录关键字小的记录向前移动
System.out.print("第"+(++c)+"次交换后:");
display();
i++;
}
// 2.1 从前到后,选择第一恶比支点大的元素
while (i < j && pivot.key.compareTo(r[i].key) > 0) {
i++;
}
// 2.2 将前面较大的元素,移到后面去
if (i < j) {
r[j] = r[i]; //将比支点记录关键字大的记录向后移动
System.out.print("第"+(++c)+"次交换后:");
display();
j--;
}
}
r[i] = pivot; //支点记录到位
System.out.print("一趟完成: ");
display();
return i; //返回支点位置
}2.2 完整快排
//【算法】 递归形式的快速排序算法
//对子表r[low..high]快速排序
public void qSort(int low, int high) {
if (low < high) {
int pivotloc = Partition(low, high); // 一趟排序,将排序表分为两部分
qSort(low, pivotloc - 1); // 低子表递归排序
qSort(pivotloc + 1, high); // 高子表递归排序
}
}
//【算法完整快排】顺序表快速排序算法
public void quickSort() {
qSort(0, this.curlen - 1);
}七、归并排序:归并排序【稳定排序方法】
1.概述
归并排序是建立在归并操作上的一种有效,稳定的排序算法。是将合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。已有序的子序列
归并排序:将两个或两个以上的有序表合并成一个新的有序表。
归并排序分类:
1. 二路归并排序
2. 多路归并排序
2.算法实现
2.1 两个相邻有序序列归并:算法
/**
*
* @param r 待排序的数组(多个有序子序列)
* @param order 已经排序号的数组
* @param h 第一个子序列开始的位置
* @param m 第一个子序列结束的位置,第二个子序列开始的位置为m+1
* @param t 第二个子序列结束的位置
*/
//【算法】两个有序序列的归并算法
//把r数组中两个相邻的有序表r[h]~r[m]和r[m+1]~r[t]归并为一个有序表order[h]~order[t]
public void merge(RecordNode[] r, RecordNode[] order, int h, int m, int t) {
int i = h, j = m + 1, k = h;
while (i <= m && j <= t) { // 将r中两个相邻子序列归并到order中
if (r[i].key.compareTo(r[j].key) <= 0) {// 较小值复制到order中
order[k++] = r[i++];
} else {
order[k++] = r[j++];
}
}
while (i <= m) { // 将前一个子序列剩余元素复制到order中
order[k++] = r[i++];
}
while (j <= t) { // 将后一个子序列剩余元素复制到order中
order[k++] = r[j++];
}
}2.1 一趟归并:算法
//【算法】一趟归并算法
//把数组r[n]中每个长度为s的有序表两两归并到数组order[n]中
//s 为子序列的长度,n为排序序列的长度
public void mergepass(RecordNode[] r, RecordNode[] order, int s, int n) {
System.out.print("子序列长度s=" + s + " ");
int p = 0; //p为每一对待合并表的第一个元素的下标,初值为0
while (p + 2 * s - 1 <= n - 1) { //两两归并长度均为s的有序表
merge(r, order, p, p + s - 1, p + 2 * s - 1);
p += 2 * s;
}
if (p + s - 1 < n - 1) { //归并最后两个长度不等的有序表
merge(r, order, p, p + s - 1, n - 1);
} else {
for (int i = p; i <= n - 1; i++) //将剩余的有序表复制到order中
{
order[i] = r[i];
}
}
}2.1 二路归并: 算法
//打印方法
public void display(RecordNode[] arr) { //输出数组元素
for (int i = 0; i < arr.length; i++) {
String str = arr[i].key.toString().length() == 1 ? " " : " ";
System.out.print(str + arr[i].key.toString());
}
System.out.println();
}
//【算法】2-路归并排序算法
public void mergeSort() {
System.out.println("归并排序");
int s = 1; // s为已排序的子序列长度,初值为1
int n = this.curlen;
RecordNode[] temp = new RecordNode[n]; // 定义长度为n的辅助数组temp
while (s < n) {
mergepass(r, temp, s, n); // 一趟归并,将r数组中各子序列归并到temp中
display(temp); // 打印temp临时数组
s *= 2; // 子序列长度加倍,下一趟归并
mergepass(temp, r, s, n); // 将temp数组中各子序列再归并到r中
display(); // 打印r数组
s *= 2;
}
}写到最后
四季轮换,已经数不清凋零了多少, 愿我们往后能向心而行,一路招摇胜!
🐋 你的支持认可是我创作的动力
💟 创作不易,不妨点赞💚评论❤️收藏💙一下
😘 感谢大佬们的支持,欢迎各位前来不吝赐教


![[Spring MVC3]MyBatis详解](https://img-blog.csdnimg.cn/b73dc86500c74b6cb3b4f9ef38d0ab77.png)