给你一个数组 rectangles ，其中 rectangles[i] = [x_i, y_i, a_i, b_i] 表示一个坐标轴平行的矩形。这个矩形的左下顶点是 (x_i, y_i) ，右上顶点是 (a_i, b_i) 。

如果所有矩形一起精确覆盖了某个矩形区域，则返回 true ；否则，返回 false 。

示例 1：

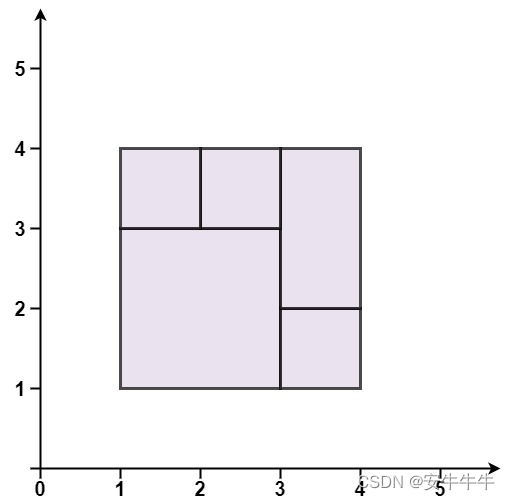
输入：rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
输出：true
解释：5 个矩形一起可以精确地覆盖一个矩形区域。 

示例 2：

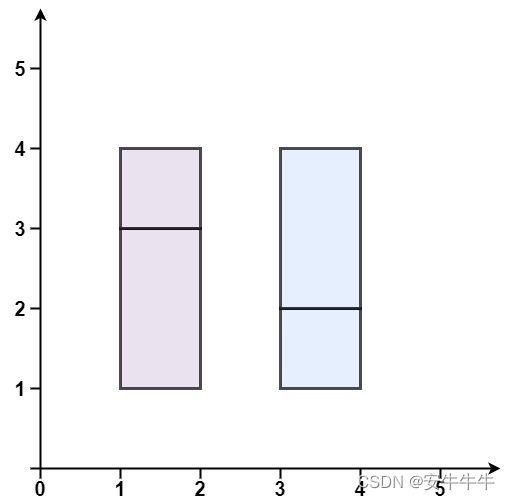
输入：rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
输出：false
解释：两个矩形之间有间隔，无法覆盖成一个矩形。

示例 3：

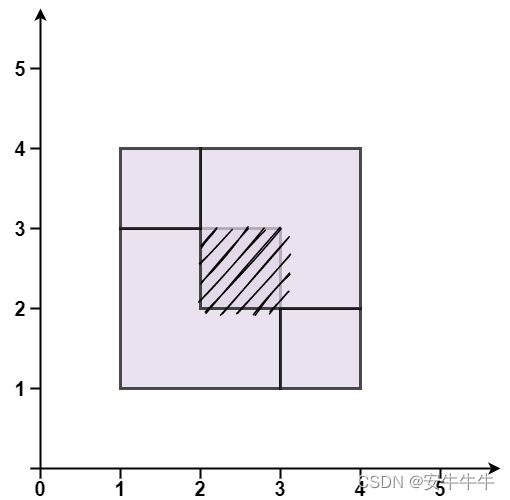
输入：rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
输出：false
解释：因为中间有相交区域，虽然形成了矩形，但不是精确覆盖。

提示：

• 1 <= rectangles.length <= 2 * 10⁴
• rectangles[i].length == 4
• -10⁵ <= x_i, y_i, a_i, b_i <= 10⁵

思路：
方案一：扫描线的思想
一个完美矩形的充要条件为：对于完美矩形的每一条非边缘的竖边，都「成对」出现（存在两条完全相同的左边和右边重叠在一起）；对于完美矩形的两条边缘竖边，均独立为一条连续的（不重叠）的竖边。

如图（红色框的为「完美矩形的边缘竖边」，绿框的为「完美矩形的非边缘竖边」）：

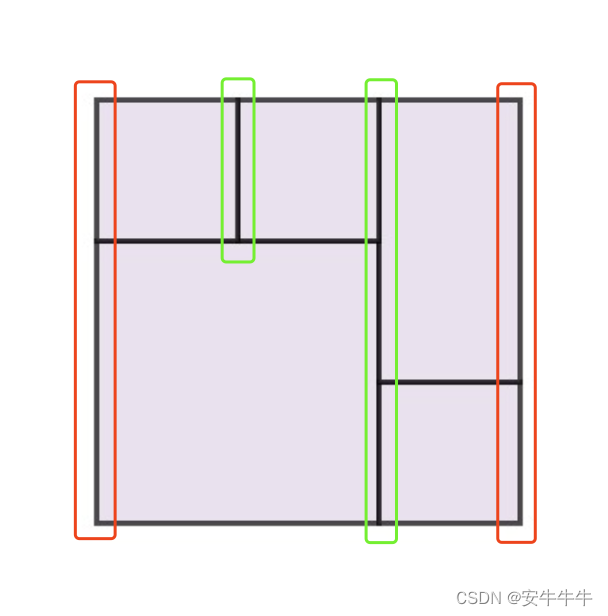
首尾相连的两条竖线（要同为左边或右边）看成一条
绿色：非边缘竖边必然有成对的左右两条完全相同的竖边重叠在一起；
红色：边缘竖边由于只有单边，必然不重叠，且连接成一条完成的竖边。

将每个矩形 rectangles[i] 看做两条竖直方向的边，使用 (x, y1, y2) 的形式进行存储（其中 y1 代表该竖边的下端点，y2 代表竖边的上端点），同时为了区分是矩形的左边还是右边，再引入一个标识位，即以四元组 (x, y1, y2, flag) 的形式进行存储。
保存所有竖边，按 x 从小到大，若 x 相等按 y1 从小到大进行排序。

遍历所有竖边。每次处理 x 坐标相同的一批竖边，判断是否符合条件

// 时间复杂度O(nlogn)
bool isRectangleCover(vector<vector<int>>& rectangles) {
    int n = rectangles.size() * 2;
    vector<vector<int>> rs;
    for (auto &rect : rectangles) {
        rs.push_back({rect[0], rect[1], rect[3], 1});
        rs.push_back({rect[2], rect[1], rect[3], -1});
    }
    sort(rs.begin(), rs.end(), [](vector<int>& a, vector<int> &b) -> bool {
        return a[0] < b[0] || (a[0] == b[0] && a[1] < b[1]);
    });

    vector<vector<int>> l1, l2;
    for (int l = 0; l < n;) {
        int r = l;
        l1.clear();
        l2.clear();
        while (r < n && rs[r][0] == rs[l][0]) { // 找到横坐标相同的线
            r++;
        }
        for (int i = l; i < r; i++) { // 处理横坐标相同的线
            vector<int> cur = {rs[i][1], rs[i][2]};
            auto &lis = rs[i][3] == 1 ? l1 : l2;
            if (lis.empty()) {
                lis.push_back(cur);
            } else {
                vector<int> &prev = lis.back();
                if (cur[0] < prev[1]) { // 当前线的下端 y 坐标小于上一根线的上端的 y 坐标
                    return false;
                } else if (cur[0] == prev[1]) { // 当前线的下端 y 坐标等于上一根线的上端的 y 坐标，合并为一条线
                    prev[1] = cur[1];
                } else {
                    lis.push_back(cur); // 当前线和上一根线之间空了一块，也是有可能的
                }
            }
        }
        if (l > 0 && r < n) { // 非边缘竖边
            if (l1.size() != l2.size()) 
                return false;
            for (int i = 0; i < l1.size(); i++) {
                if (l1[i][0] != l2[i][0] || l1[i][1] != l2[i][1])
                    return false;
            }
        } else { // 边缘竖边
            if (l1.size() + l2.size() != 1) {
                return false;
            }
        }
        l = r;
    }
    return true;
}

方案二：用点来表示整幅图。
每个矩形的左下角值为 1，左上角值为 -1，右下角值为 -1，右上角值为 1。空白区域的值为 0

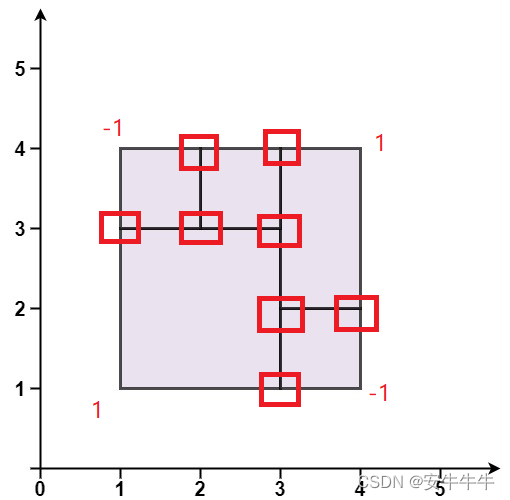
图中红色方框内的顶点值的和都为 0

一个完美矩形，除了最外面四个角以外，其它所有的顶点和都为0。
遍历所有矩形的顶点，计算顶点和。当只有 4 个不为 0 的顶点且这 4 个顶点必须是 1 或 -1 时，矩形是完美矩形。

// O(n)的时间复杂度
bool isRectangleCover(vector<vector<int>>& rectangles) {
    unordered_map<long long, int> mark;
    const long long N = 1000000; // 用单个值表示坐标，用 x 乘一个大于 y 的取值范围的值，然后加 y
    for (auto &rect : rectangles) {
        int x1 = rect[0], y1 = rect[1];
        int x2 = rect[2], y2 = rect[3];
        mark[x1 * N + y1]++; // 左下角是 1
        mark[x1 * N + y2]--; // 左上角是 -1
        mark[x2 * N + y1]--; // 右下角是 -1
        mark[x2 * N + y2]++; // 右上角是 1；
    }
    int n_mark = 0;
    for (auto &ptr : mark) {
        if (ptr.second != 0) {
            if (abs(ptr.second) != 1) {
                return false;
            }
            n_mark++;
        }
    }
    return n_mark == 4;
}