题目来源

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目描述

在一个 n * m 的二维数组中，每一行都按照从左到右 非递减 的顺序排序，每一列都按照从上到下 非递减 的顺序排序。请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

示例

现有矩阵 matrix 如下：

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

给定 target = 5，返回 true。

给定 target = 20，返回 false。

题目分析

根据题意，判断 target 是否存在于二维数组中，简单粗暴的方法就是暴力法，两层循环遍历，然后依判断每个元素是否与 target 相等，但是这样做效率很差，最坏情况下，需要 O(NM) 的时间复杂度，N 为二维数组的行数，M 为二维数组的列数。
由题可知，每一行或每一列的元素按照递增的的顺序排序，根据元素的顺序特点，我们可以使用二分法进行算法优化，先遍历行或者列，再对列或者行进行二分查找，提高查询效率。
逆时针 45° 翻转矩阵，如下图所示，观察元素由上而下的特点，类似一颗 二叉搜索树 (BST)，3 为根节点，左分支 2 比 3 小，右分支 6 比 3 大，根据这个特点，可以再次优化算法，提高查询效率。

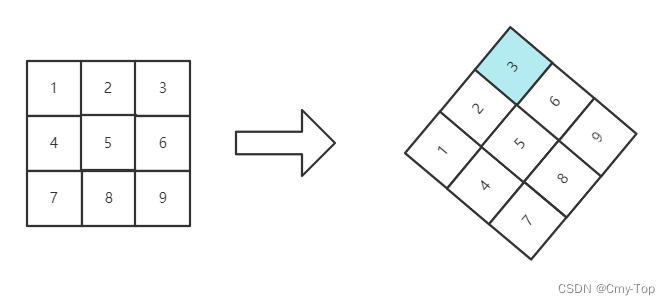
算法

暴力法

通过两次循环遍历，依次判断二维数组中的元素是否等于 target，相等则返回 true，否则返回 false

代码实现

func findNumberIn2DArray(matrix [][]int, target int) bool {
	for i := 0; i < len(matrix); i++ {
		for j := 0; j < len(matrix[i]); j++ {
			if matrix[i][j] == target {
				return true
			}
		}
	}
	return false
}

复杂度分析

时间复杂度：O(NM)，其中 N 为矩阵行数，M 为矩阵列数。
空间复杂度：O(1)，没有使用额外的内存空间。

二分法

先循环遍历行
初始化左边界 left 和右边界 right，对列进行二分查找
- 计算中间值 mid
- 判断 mid 是否等于 target ，等于则返回 true
- 当 mid 大于 target 时，左边界 left 向右移动，移动到 mid + 1 的位置
- 当 mid 小于 target 时，右边界 right 向左移动，移动到 mid - 1 的位置
- 循环结束之后，没有找到与 target 相等的元素，返回 false

代码实现

func findNumberIn2DArray(matrix [][]int, target int) bool {
    for _, nums := range matrix {
        left, right := 0, len(nums) - 1
        for left <= right {
            mid := (left + right) / 2
            if target == nums[mid] {
                return true
            }
            if nums[mid] > target {
                right = mid - 1 
            } else {
                left = mid + 1
            }
        }
    }
    return false
}

复杂度分析

时间复杂度：O(NlogM)，其中 N 为矩阵行数，M 为矩阵列数，此算法最多循环 N * logM 次。
空间复杂度：O(1)，没有使用额外的内存空间。

模拟 BST 标记查找法

matrix = [[1, 2,3],[4, 5,6],[7, 8,9]]，target = 4

对二维数组进行判空，空则返回 false
初始化 i = 0, j = len(matrix[0]) - 1 = 2，将标记点设置为 6，开始遍历，标记点与 target 进行比较
- 当 matrix[i][j] == target 时，找到目标值，返回 true
- 当 if matrix[i][j] > target 时，j--，将标记点左下移动
- 当 matrix[i][j] < target 时，i++，将标记点右下移动
遍历结束后，未找到目标值，返回 false

代码实现

func findNumberIn2DArray(matrix [][]int, target int) bool {
    if len(matrix) == 0 {
        return false
    }
	for i, j := 0, len(matrix[0])-1; i <= len(matrix) - 1 && j >= 0; {
		if matrix[i][j] == target {
			return true
		}
		if matrix[i][j] > target {
			j--
		} else {
			i++
		}
	}
	return false
}