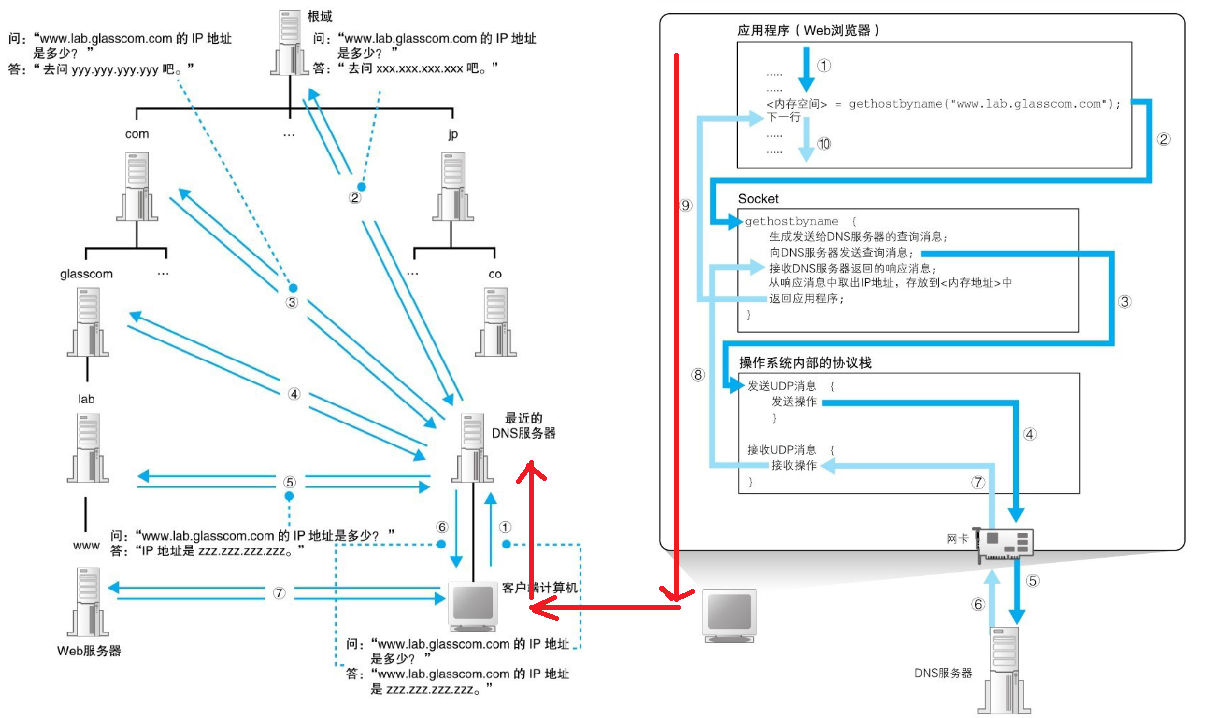
朴素贝叶斯是基于概率论统计学的分类算法。

贝叶斯理论是指根据一个已发生事件的概率，计算另一个事件的发生概率。

目录

1.相关概念 

1.1先验概率

应用举例

1.2条件概率

应用举例

1.3全概率公式

应用举例 

1.4后验概率 

应用举例 

2.课堂笔记  ​

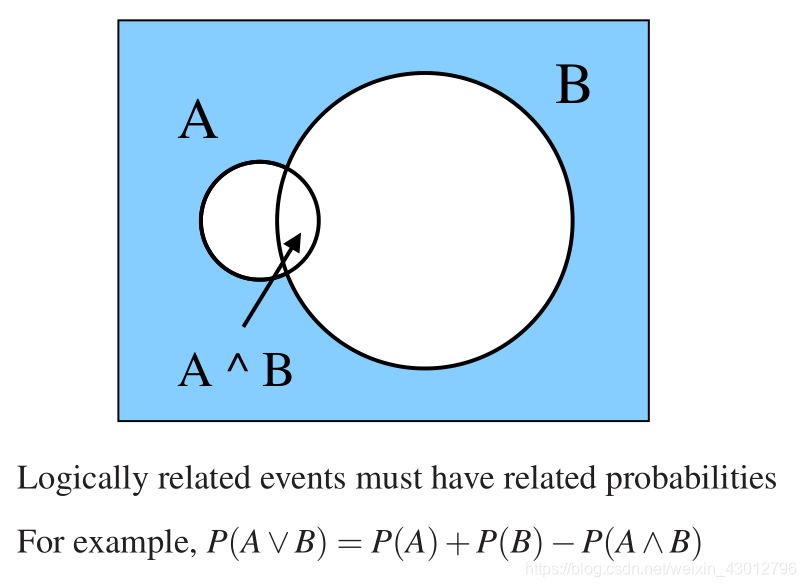
3.文氏图

---

 1.相关概念 

1.1先验概率

指根据以往的经验和分析得到的概率。

应用举例

该公园中男女比例通常为2:1；根据这一以往经验求得：

；而先验概率和需要通过全概率公式计算求解。

1.2条件概率

指在某一事件已经发生的条件下，另一个事件发生的概率。

应用举例

该公园男性穿凉鞋的概率为1/2，女性穿凉鞋的概率为2/3，即 和 

1.3全概率公式

如果事件构成一个完备事件组，即它们两两互不相容，互相独立，其和为全集。

应用举例 

可以根据全概率公式求出公园里男性穿凉鞋的概率和男性穿凉鞋的概率。

1.4后验概率 

与先验概率相对应，某事件已经发生，另一个事件因为它发生而发生的概率。

应用举例 

而朴素贝叶斯算法正是利用以上信息求解后验概率，并且依据后验概率的值来进行分类。

得知某人穿着凉鞋，想求出他为男性还是女性的概率。

2.课堂笔记

也就是说，在知道一个人穿凉鞋的前提下，这个人是男性的概率是3/5；是女性的概率是2/5。如果问题是“判断该人是男性还是女性”，此问题就是一个分类问题。由于依据贝叶斯公式计算的后验概率是男性的概率大于是女性的概率，那么我们就可以将其分类为男性(实际在使用朴素贝叶斯进行分类时，不需要求解分母)因为，两个概率的分母相同，不除以分母，相对大小也不会发生变化。——————>天气预测问题/垃圾邮件分类问题

3.文氏图