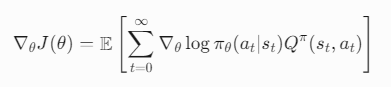迁移学习上的一个老问题,怎么做多领域的迁移?以前的逻辑认为领域迁移属于是对参数做方向性的调整,如果两个领域方向相左,实际上不管怎么加权相加都是不合理的。
目前一些做法想着去观察LoRA权重矩阵中的稠密块与稀疏块,选择稠密的部分予以保留,稀疏的部分予以舍弃,然后有选择地进行合并,这是一种很模糊的做法,实际上也缺乏理论保证,而且,低秩与稀疏通常并不等价。
假定是做秩一分解:
h 1 = W 0 x + ( B 1 A 1 ) x = W 0 x + ( ∑ i = 1 r 1 d 1 i v i v i ⊤ ) x = W 0 x + ∑ i = 1 r 1 ( d 1 i v i ⊤ x ) v i = W 0 x + ∑ i = 1 r 1 k 1 i v i h 2 = W 0 x + ( B 2 A 2 ) x = W 0 x + ( ∑ i = 1 r 2 d 2 i u i u i ⊤ ) x = W 0 x + ∑ i = 1 r 2 ( d 2 i v i ⊤ x ) v i = W 0 x + ∑ i = 1 r 2 k 2 i v i h_1 = W_0 x + (B_1A_1) x = W_0 x + \left(\sum_{i=1}^{r_1} d_{1i} v_iv_i^\top\right) x = W_0 x + \sum_{i=1}^{r_1} (d_{1i} v_i^\top x) v_i = W_0 x + \sum_{i=1}^{r_1} k_{1i} v_i \\ h_2 = W_0 x + (B_2A_2) x = W_0 x + \left(\sum_{i=1}^{r_2} d_{2i} u_iu_i^\top\right) x = W_0 x + \sum_{i=1}^{r_2} (d_{2i} v_i^\top x) v_i = W_0 x + \sum_{i=1}^{r_2} k_{2i} v_i h1=W0x+(B1A1)x=W0x+(i=1∑r1d1ivivi⊤)x=W0x+i=1∑r1(d1ivi⊤x)vi=W0x+i=1∑r1k1ivih2=W0x+(B2A2)x=W0x+(i=1∑r2d2iuiui⊤)x=W0x+i=1∑r2(d2ivi⊤x)vi=W0x+i=1∑r2k2ivi
调整的其实就是rank数量的单位向量的加权和。
这里面的 u i , v i u_i,v_i ui,vi都是单位向量, d 1 i d_{1i} d1i和 d 2 i d_{2i} d2i表示奇异值。
k 1 i k_{1i} k1i和 k 2 i k_{2i} k2i都是标量。
那么我们可以在每一层的输出时,选择需要保留的若干个单位向量的加权和作为这层的输出,保留的依据可以根据 k 1 i k_{1i} k1i和 k 2 i k_{2i} k2i的大小来确定(保大去小)。
比如在合并的时候从 r 1 + r 2 r_1+r_2 r1+r2个秩一矩阵中取 r 1 + r 2 2 \frac{r_1+r_2}{2} 2r1+r2个出来作为融合后的LoRA
这样的调整本身关于输入 x x x是动态的,复杂度很差。
另一件事就是白盒压缩、或者说模型压缩的时候,为什么不直接用SVD进行降维处理呢,重新训练一个小模型出来,可能连模型结构都不一样的模型出来替代原模型,难道还能比跟原模型结构相同的东西有更令人信服的性能吗?
题外话,以及做INT量化与用SVD进行降维处理,两种方法截然不同,对精度的影响有何区别呢?两者都对隐层权重的数值,从而影响每个隐层的输出,但是直觉上,INT量化产生的误差的方差在point-wise上是处处相等的(即均匀误差),但是SVD似乎并非如此,因为SVD给出的误差其实是若干个比较小的奇异值所对应的秩一矩阵的加权和,而秩一矩阵值的分布显然不可能是均匀分布,这取决于奇异向量的分布:
(1) 高度结构化
- 所有行成比例:矩阵的每一行是向量
v
v
v的标量倍数(系数为
u
i
u_i
ui)。
第 i 行 = u i ⋅ [ v 1 , v 2 , … , v n ] \text{第} i \text{行} = u_i \cdot [v_1, v_2, \dots, v_n] 第i行=ui⋅[v1,v2,…,vn] - 所有列成比例:每一列是向量
u
u
u的标量倍数(系数为
v
j
v_j
vj)。
第 j 列 = v j ⋅ [ u 1 , u 2 , … , u m ] T \text{第} j \text{列} = v_j \cdot [u_1, u_2, \dots, u_m]^T 第j列=vj⋅[u1,u2,…,um]T
(2) 数值分布依赖基向量
- 矩阵元素的值完全由
u
u
u和
v
v
v的分布决定:
- 若 u u u或 v v v服从高斯分布,则 M i j M_{ij} Mij是高斯变量的乘积(分布可能复杂,但通常呈现尖峰、重尾特性)。
- 若 u u u或 v v v是稀疏的,则 M M M也会稀疏。
(3) 特征值与奇异值
- 非零特征值:秩1矩阵仅有1个非零特征值(等于 u T v u^T v uTv或 v T u v^T u vTu)。
- 奇异值:唯一非零奇异值为 ∥ u ∥ ⋅ ∥ v ∥ \|u\| \cdot \|v\| ∥u∥⋅∥v∥,其余奇异值为0。
至少从误差的分布上来说,量化要更稳定可控一些。
总是觉得现在人做事太简单粗暴了,没有理论分析的支撑,全凭拍脑袋。
下面简单看一看DeepSeek对于多LoRA合并的论述:
多LoRA并行(Multiple LoRA Adapters Parallel)的底层逻辑涉及在模型运行时动态组合多个低秩适配器的权重,其核心是通过并行计算或权重叠加的方式将不同LoRA模块的影响同时作用于基座模型(Base Model)。
1. 基本概念回顾
- LoRA的本质:
在原始模型权重 W 0 ∈ R d × k W_0 \in \mathbb{R}^{d \times k} W0∈Rd×k 旁注入低秩矩阵 A ∈ R d × r A \in \mathbb{R}^{d \times r} A∈Rd×r 和 B ∈ R r × k B \in \mathbb{R}^{r \times k} B∈Rr×k,其中 r ≪ min ( d , k ) r \ll \min(d,k) r≪min(d,k)。
前向传播时,输出为:
h = W 0 x + ( B A ) x h = W_0 x + (BA) x h=W0x+(BA)x - 多LoRA并行:
同时激活多个LoRA模块(如 B A ( 1 ) + B A ( 2 ) + … BA^{(1)} + BA^{(2)} + \dots BA(1)+BA(2)+…),输出变为:
h = W 0 x + ∑ i = 1 N ( B ( i ) A ( i ) ) x h = W_0 x + \sum_{i=1}^N (B^{(i)} A^{(i)}) x h=W0x+i=1∑N(B(i)A(i))x
2. 运行时计算的两种实现方式
方式1:权重直接叠加(静态合并)
步骤:
- 离线合并:在加载模型时,将所有激活的LoRA的增量权重
Δ
W
i
=
B
(
i
)
A
(
i
)
\Delta W_i = B^{(i)}A^{(i)}
ΔWi=B(i)A(i) 相加:
Δ W merged = ∑ i = 1 N B ( i ) A ( i ) \Delta W_{\text{merged}} = \sum_{i=1}^N B^{(i)}A^{(i)} ΔWmerged=i=1∑NB(i)A(i) - 前向计算:仅需计算一次合并后的增量:
h = W 0 x + Δ W merged x h = W_0 x + \Delta W_{\text{merged}} x h=W0x+ΔWmergedx
底层逻辑:
- 优点:计算量与单LoRA相同,无额外开销。
- 缺点:静态合并后无法动态调整适配器组合。
- 适用场景:推理时需固定融合多个LoRA。
代码示例(PyTorch):
# 假设 lora_A 和 lora_B 是两个LoRA模块的增量权重
delta_W = lora_A @ lora_B + lora_C @ lora_D # 低秩矩阵乘法
h = base_model_W @ x + delta_W @ x
方式2:动态并行计算(运行时逐适配器计算)
步骤:
- 独立保留LoRA权重:保持每个LoRA的 A ( i ) A^{(i)} A(i) 和 B ( i ) B^{(i)} B(i) 矩阵独立存储。
- 前向传播时逐适配器计算:
h = W 0 x + ∑ i = 1 N ( B ( i ) ( A ( i ) x ) ) h = W_0 x + \sum_{i=1}^N (B^{(i)} (A^{(i)} x)) h=W0x+i=1∑N(B(i)(A(i)x))- 先计算所有 A ( i ) x A^{(i)} x A(i)x,再与对应的 B ( i ) B^{(i)} B(i) 相乘,最后累加结果。
底层逻辑:
- 优点:支持动态开关适配器(如根据输入选择不同的LoRA组合)。
- 缺点:计算量随LoRA数量线性增长(需 N N N 次低秩矩阵乘法和累加)。
- 适用场景:需要运行时灵活切换适配器的场景(如多任务推理)。
代码示例(PEFT库实现逻辑):
# 伪代码:动态多LoRA计算
h = base_layer(x)
for adapter in active_adapters:
lora_A = adapters[adapter].A # 形状 (d, r)
lora_B = adapters[adapter].B # 形状 (r, k)
h += (lora_B @ (lora_A @ x)) * adapter.scaling # 缩放系数
3. 关键优化技术
为了减少多LoRA并行的计算开销,框架(如PEFT)通常会采用以下优化:
(1) 共享基座模型权重
- 所有LoRA复用同一份 W 0 W_0 W0,仅额外存储增量部分 Δ W i \Delta W_i ΔWi。
(2) 批处理低秩计算
- 将多个LoRA的
A
(
i
)
A^{(i)}
A(i) 拼接为大矩阵
A
stack
∈
R
N
⋅
r
×
d
A_{\text{stack}} \in \mathbb{R}^{N \cdot r \times d}
Astack∈RN⋅r×d,通过一次矩阵乘法和分割结果加速计算:
[ A ( 1 ) x ; A ( 2 ) x ; … ] = A stack x [A^{(1)}x; A^{(2)}x; \dots] = A_{\text{stack}} x [A(1)x;A(2)x;…]=Astackx
再分别与对应的 B ( i ) B^{(i)} B(i) 相乘。
(3) 延迟缩放(Scaling)
- 将LoRA的缩放系数
α
r
\frac{\alpha}{r}
rα 合并到
B
(
i
)
B^{(i)}
B(i) 中,避免重复乘法:
B ′ ( i ) = B ( i ) ⋅ α r B'^{(i)} = B^{(i)} \cdot \frac{\alpha}{r} B′(i)=B(i)⋅rα
4. 数学形式对比
假设有两个LoRA( Δ W 1 = B 1 A 1 \Delta W_1 = B_1A_1 ΔW1=B1A1, Δ W 2 = B 2 A 2 \Delta W_2 = B_2A_2 ΔW2=B2A2):
| 方法 | 计算过程 | FLOPs |
|---|---|---|
| 静态合并 | h = W 0 x + ( B 1 A 1 + B 2 A 2 ) x h = W_0 x + (B_1A_1 + B_2A_2) x h=W0x+(B1A1+B2A2)x | O ( d k + d r + r k ) O(dk + dr + rk) O(dk+dr+rk) |
| 动态并行 | h = W 0 x + B 1 ( A 1 x ) + B 2 ( A 2 x ) h = W_0 x + B_1(A_1 x) + B_2(A_2 x) h=W0x+B1(A1x)+B2(A2x) | O ( d k + 2 ( d r + r k ) ) O(dk + 2(dr + rk)) O(dk+2(dr+rk)) |
| 批处理优化 | h = W 0 x + [ B 1 , B 2 ] ⋅ [ A 1 ; A 2 ] x h = W_0 x + [B_1, B_2] \cdot [A_1; A_2] x h=W0x+[B1,B2]⋅[A1;A2]x | O ( d k + d ( 2 r ) + ( 2 r ) k ) O(dk + d(2r) + (2r)k) O(dk+d(2r)+(2r)k) |
5. 实际框架中的实现
以PEFT(Hugging Face)为例:
- 注册多个适配器:
model.add_adapter("adapter1", lora_config_A) model.add_adapter("adapter2", lora_config_B) - 动态激活组合:
model.set_active_adapters(["adapter1", "adapter2"]) - 底层计算:
- PEFT自动选择动态并行计算(方式2),按需累加所有激活适配器的输出。
6. 总结:多LoRA并行的本质
- 静态合并:算术叠加权重,适合固定组合的轻量推理。
- 动态并行:独立计算后求和,适合灵活适配但计算成本较高。
- 优化方向:通过批处理和共享基座权重减少冗余计算。
如果需要进一步分析具体框架(如PEFT、AdaLoRA)的实现细节,可以提供更多上下文!