范数鲁棒控制器的设计
 鲁棒控制器的设计
鲁棒控制器的设计
根据双端子状态方程对象模型结构,控制器设计的目标是找到一个控制器K(s),它能保证闭环系统的
范数限制在一个给定的小整数
下,即
这时控制器的状态方程为:
其中X与Y分别为下面两个代数Riccati方程的解。
控制器存在的前提条件为:
- 在增广矩阵中,
足够小,且满足
- 控制器Riccati方程的解X为正定矩阵
- 观测器Riccati方程的解Y为正定矩阵
,即两个Riccati方程的积矩阵的所有特征值均小于
在上述前提条件下搜索最小的值,则可设计出最优
控制器。
 鲁棒控制器的实现
鲁棒控制器的实现
对双端子模型G,鲁棒控制工具箱中相应的函数可以直接用于控制器的设计,这些函数的调用格式为:
[K,CL,gamma] = h2syn(G,nmeas,ncont); % nmeas:输出信号y的个数
% ncont:控制信号u的个数
% K 为优化的控制器状态空间方程
% CL为w到z的传递函数
% gamma为CL的2范数
[K,CL,gamma] = hinfsyn(G,nmeas,ncont); % nmeas:输出信号y的个数
% ncont:控制信号u的个数
% K 为优化的控制器状态空间方程
% CL为w到z的传递函数
% gamma为CL的无穷范数
其中控制系统的双端子模型如下所示。

例如:
考虑一下对象模型:
试用MATLAB鲁棒控制函数设计控制器。
首先利用MATLAB函数h2syn计算在优化 norm下的控制器。
MATLAB代码如下:
clear all;clc;
num=300;
den=[1 1.5 300];
G=tf(num,den);
s=tf('s');
W1=100*(0.06*s+1)^2/(0.3*s+1)^2;
W2=1;
W3=s^2/3000;
Tss=augtf(G,W1,W2,W3);
[K,CL,gamma]=h2syn(Tss);
Gc=feedback(G,K);
step(feedback(G*tf(K),1))
grid on程序运行结果为:
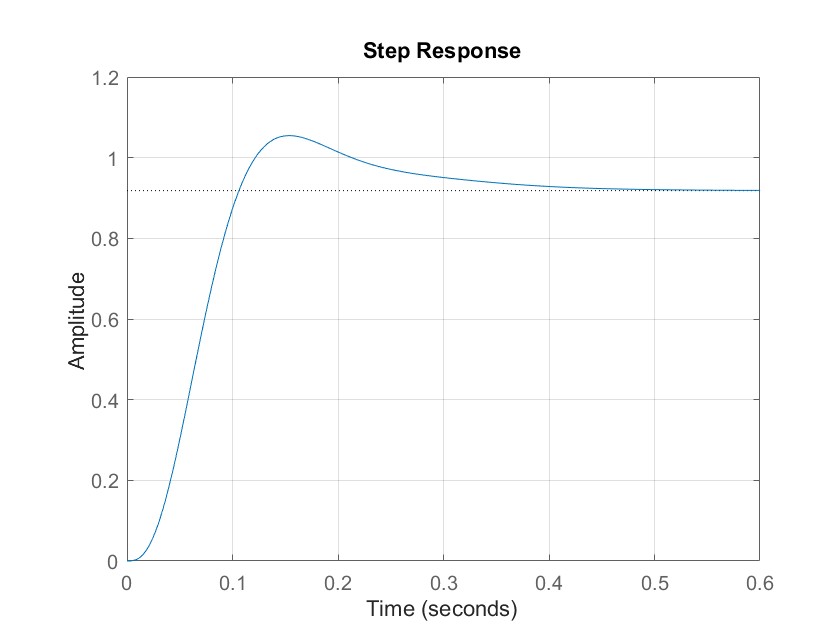
其次利用MATLAB函数hinfsyn计算在优化 norm下的控制器。
MATLAB代码如下:
clear all;clc;
num=300;
den=[1 1.5 300];
G=tf(num,den);
s=tf('s');
W1=100*(0.06*s+1)^2/(0.3*s+1)^2;
W2=1;
W3=s^2/3000;
Tss=augtf(G,W1,W2,W3);
[K,CL,gamma]=hinfsyn(Tss);
Gc=feedback(G,K);
step(feedback(G*tf(K),1))
grid on程序运行结果为:
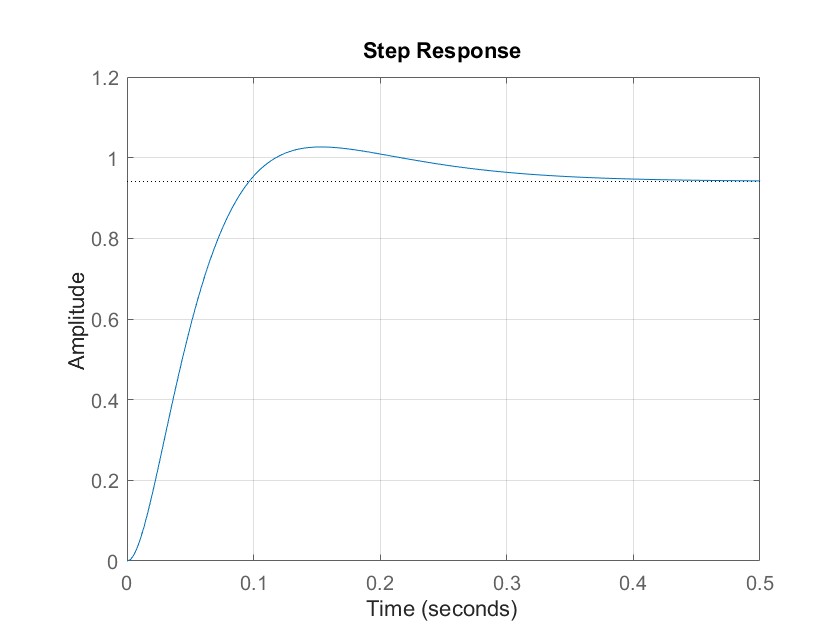
如果知道了控制器,大家可以
- 画出闭环系统的传递函数
- 引入模型不确定性,然后观察系统响应
- 观察输入信号曲线,进而判断控制器的可行性
最后,欢迎大家有问题给我留言。
非常感谢小伙伴们的-点赞-收藏-加关注。