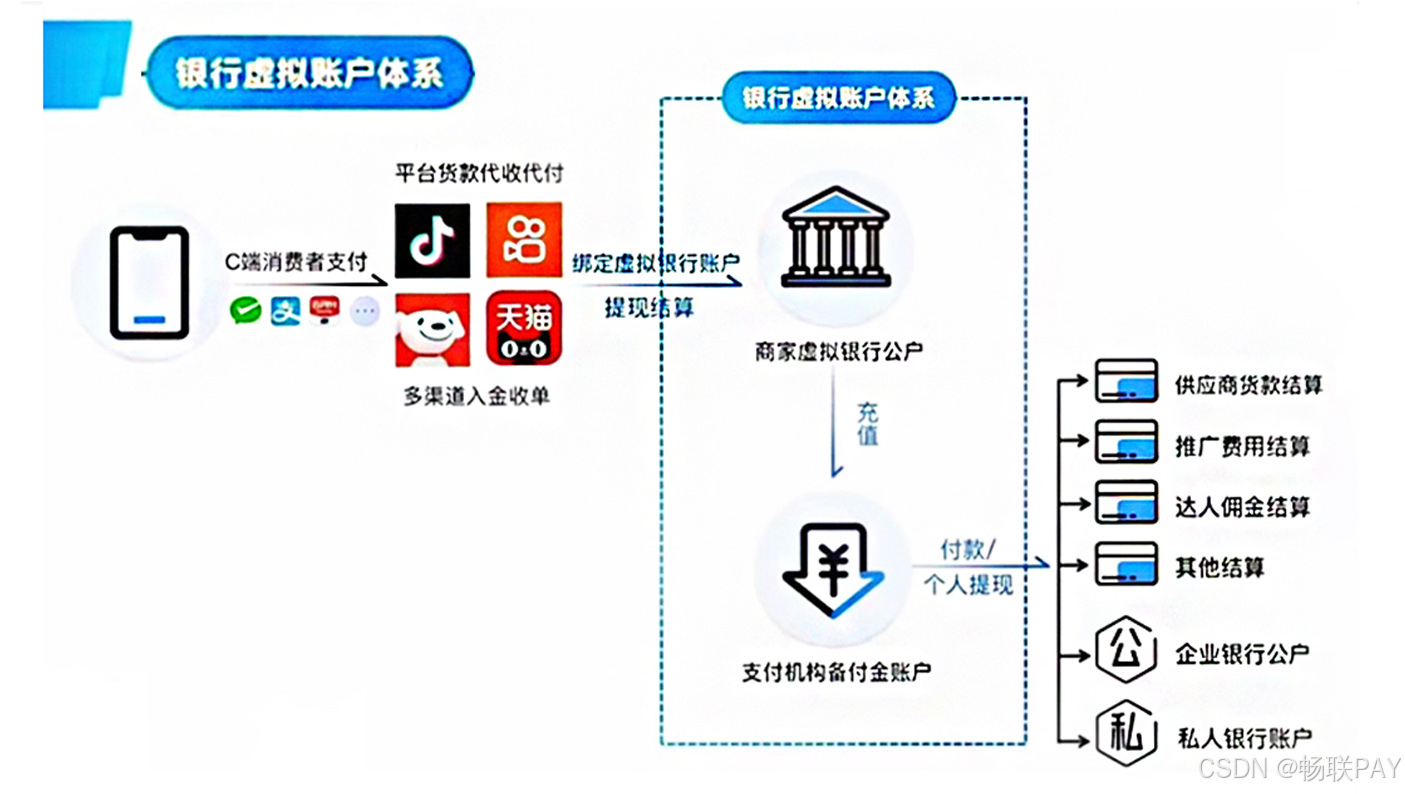
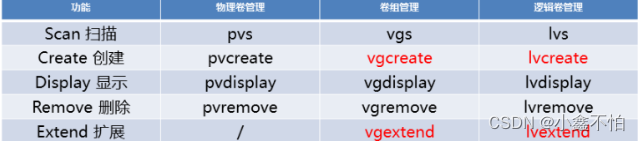
题目描述

思路

让求包含这n个整数的最短等差数列，既让包含这几个数，项数最少，若项数最少，肯定不能添加小于最小的和大于最大的，而且让项数最小，公差得大
等差数列的公差aj - ai / j - i; 这又是一个等差数列，即任意两项的差为公差d的倍数，如果要包含所有的，相当于求相邻两项差的最大公约数

竟然转化为了数学问题，拿到问题先分析！！不要急着做，正面分析不出来分析对立

代码

要记得先排序！！为了避免差为负的

最大公约数不可能为负数！

而且要考虑边界情况，万一这几个数都一样，那差值就是0，__gcd不能求为0的情况，边界！！！

#include<bits/stdc++.h>

using namespace std;

const int N = 1e5+10;

int a[N];
int s[N];
int main()
{
	int n;
	cin >> n;
	for(int i = 1; i <= n ; i++)
		cin >> a[i];
	sort(a+1, a + n + 1);
	if(a[2] == a[1]) //表示不一样
	{
		cout<<n<<endl;
		return 0;
	}
	for(int i = 2; i <= n; i++)
	{
		s[i-1] = a[i] - a[i - 1]; //构建差分矩阵
	}
	int res = 0;
	int ans = 0;
	ans = s[1];
	for(int i = 2; i <= n; i++)
	{
		ans = __gcd(s[i], ans); //求最大公约数
	}
//	cout<<ans<<endl;
//	cout<<a[n]<<endl;
//	cout<<a[1]<<endl;
	cout<<(a[n] - a[1] )/ ans + 1 <<endl;
	return 0;
}

总结

要认真分析，有个思路再去考虑可行性，以及要考虑边界情况，通过这道题学到了

__gcd求公约数得>= 1，公约数不能是负数或0