1、下载并安装Ollama

官方网址：Ollama

安装好后，在命令行输入，

ollama --version

返回以下信息，则表明安装成功，

2、 下载AI大模型

这里以deepseek-r1:1.5b模型为例，

在命令行中，执行，

ollama run deepseek-r1:1.5b

模型下载到本地后，便可直接使用，

3、 下载并安装docker

官方网址：Docker: Accelerated Container Application Development

安装好后，在命令行输入，

docker -v

返回以下信息，表明安装成功，

4、拉取Open WebUI的镜像并部署

执行以下命令，

docker run -d -p 3000:8080 --add-host=host.docker.internal:host-gateway -v open-webui:/app/backend/data --name open-webui --restart always ghcr.io/open-webui/open-webui:main

返回以下信息表明成功拉取镜像，

随后，在docker中会出现名为open-webui的容器，

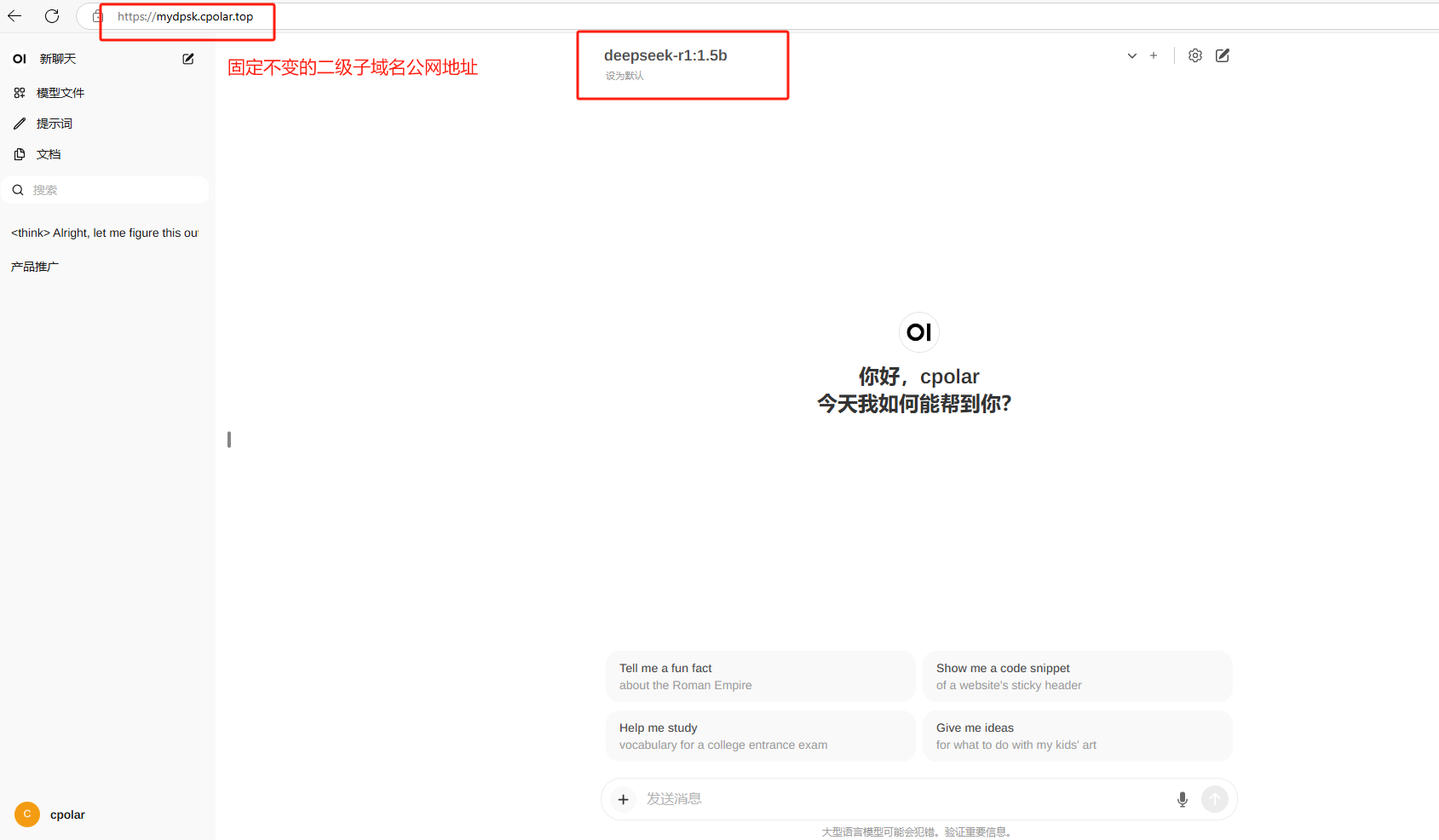
鼠标点击3000:8080，便可跳转到Open-WebUI的认证界面，注册后便可与大模型聊天，