在数据挖掘和机器学习领域,聚类是一种常见的无监督学习方法,用于将数据点划分为不同的组或簇。K均值聚类算法是其中一种简单而有效的聚类算法。今天,我将通过一个具体的Python代码示例,向大家展示如何实现K均值聚类算法,并通过可视化的方式呈现聚类过程。
1. K均值聚类算法简介
K均值聚类算法是一种划分方法,它将数据集划分为K个簇。算法的基本思想是:首先随机选择K个数据点作为初始聚类中心,然后计算每个数据点与这些聚类中心的距离,将数据点分配到最近的聚类中心所在的簇中。接着,根据每个簇中的数据点重新计算聚类中心,重复上述过程,直到聚类中心不再发生变化或达到设定的迭代次数。
2. 数据准备
在本例中,我们手动创建了四类数据点,每类数据点都具有一定的分布规律。这些数据点将作为我们聚类的对象。以下是数据点的代码定义:
class1_points = np.array([[1.9, 1.2],
[1.5, 2.1],
[1.9, 0.5],
[1.5, 0.9],
[0.9, 1.2],
[1.1, 1.7],
[1.4, 1.1]])
class2_points = np.array([[-1.9, 1.2],
[-1.5, 2.1],
[-1.9, 0.5],
[-1.5, 0.9],
[-0.9, 1.2],
[-1.1, 1.7],
[-1.4, 1.1]])
class3_points = np.array([[1.9, -1.2],
[1.5, -2.1],
[1.9, -0.5],
[1.5, -0.9],
[0.9, -1.2],
[1.1, -1.7],
[1.4, -1.1]])
class4_points = np.array([[-1.9, -1.2],
[-1.5, -2.1],
[-1.9, -0.5],
[-1.5, -0.9],
[-0.9, -1.2],
[-1.1, -1.7],
[-1.4, -1.1]])我们将这四类数据点合并为一个数据集,用于后续的聚类操作:
data = np.concatenate((class1_points,class2_points,class3_points,class4_points))3. 聚类过程实现
3.1 初始化聚类中心
我们设定聚类数目为2(k = 2),并从数据集中随机选择两个数据点作为初始聚类中心:
centroids = data[np.random.choice(range(len(data)),k,replace=False)]3.2 迭代聚类
在每次迭代中,我们执行以下步骤:
3.2.1 计算距离
计算每个数据点与聚类中心的距离。这里使用了欧几里得距离:
distances = np.linalg.norm(data[:,np.newaxis,:]-centroids,axis=2)3.2.2 分配数据点到最近的聚类中心
根据计算出的距离,将每个数据点分配到最近的聚类中心所在的簇中:
labels = np.argmin(distances,axis=1)3.2.3 更新聚类中心
根据每个簇中的数据点,重新计算聚类中心:
new_centroids = np.array([data[labels == i].mean(axis = 0) for i in range(k)])3.3 聚类结果可视化
在每次迭代中,我们通过matplotlib库绘制数据点、聚类中心以及数据点与聚类中心的连接线,以直观地展示聚类过程:
plt.cla()
# 绘制连接线
for i in range(k):
cluster_points = data[labels == i]
centroid = centroids[i]
for cluster_point in cluster_points:
plt.plot([cluster_point[0], centroid[0]], [cluster_point[1], centroid[1]], 'k--')
# 绘制四类点,并分别用不同颜色标出来
plt.scatter(class1_points[:, 0], class1_points[:, 1], c="red")
plt.scatter(class2_points[:, 0], class2_points[:, 1], c="blue")
plt.scatter(class3_points[:, 0], class3_points[:, 1], c="cyan")
plt.scatter(class4_points[:, 0], class4_points[:, 1], c="green")
# 绘制聚类中心点,并用圆圈标记
plt.scatter(centroids[:, 0], centroids[:, 1], c="black", marker='o', s=100, label='Centroids')
plt.pause(1)3.4 判断收敛
如果新计算的聚类中心与上一次的聚类中心完全相同,说明算法已经收敛,可以结束迭代:
if np.all(centroids == new_centroids):
break
centroids = new_centroids4. 运行结果
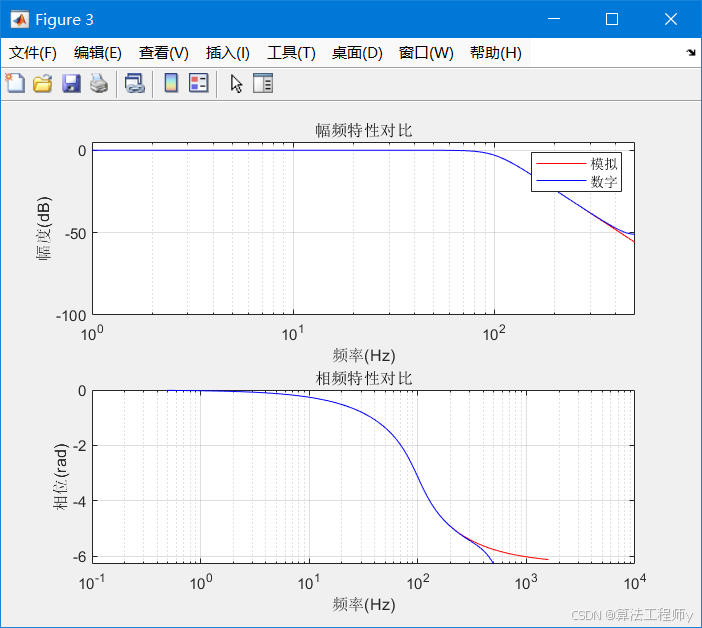
运行上述代码后,你将看到一个动态的聚类过程展示。数据点会逐渐被分配到不同的簇中,聚类中心也会不断调整,直到最终收敛。
由于点位是随机选取,所以可能会有不同的聚类结果:

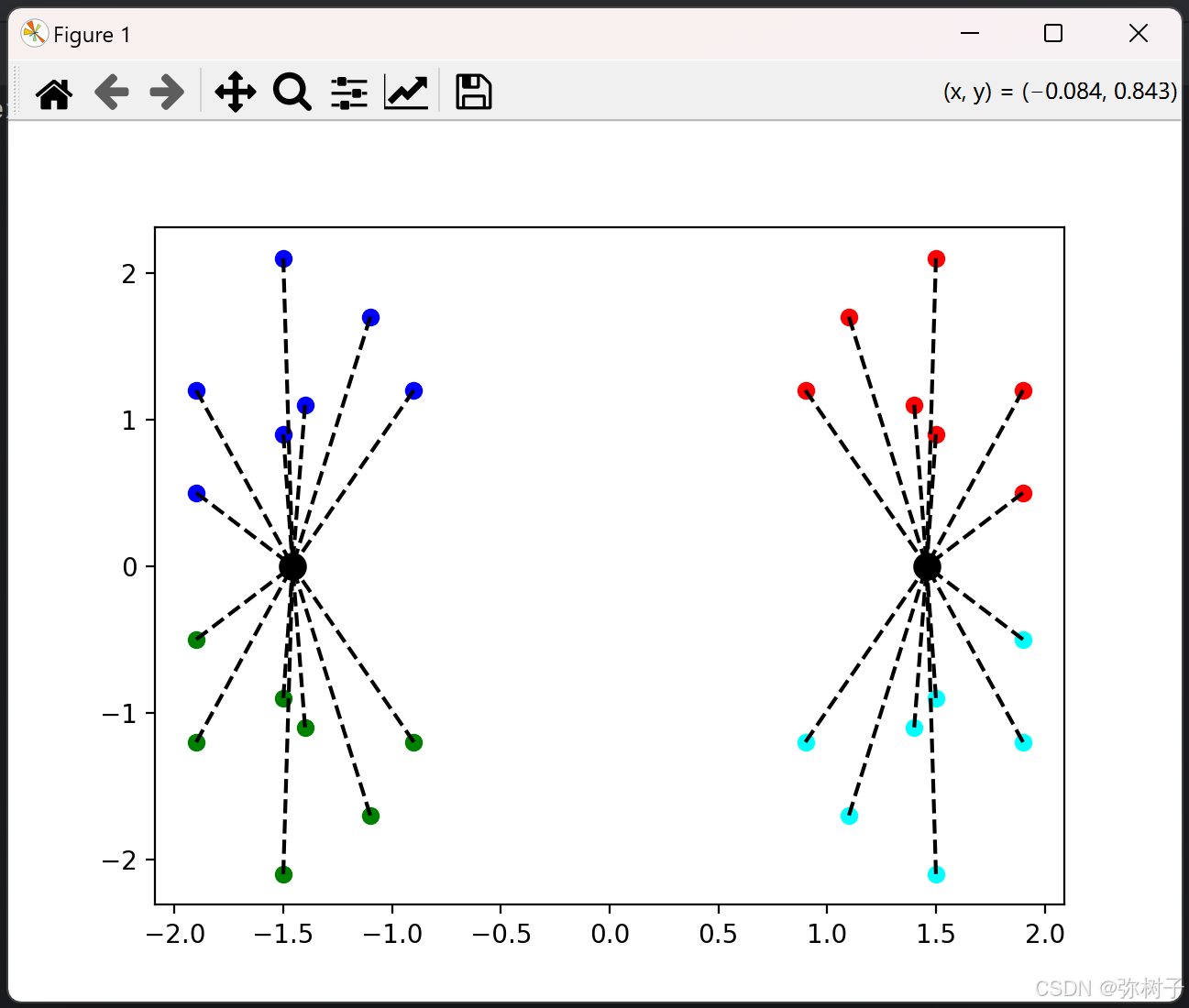
5.完整代码
import numpy as np
import matplotlib.pyplot as plt
"""数学方法实现k均值聚类"""
# 创建示例数据
class1_points = np.array([[1.9, 1.2],
[1.5, 2.1],
[1.9, 0.5],
[1.5, 0.9],
[0.9, 1.2],
[1.1, 1.7],
[1.4, 1.1]])
class2_points = np.array([[-1.9, 1.2],
[-1.5, 2.1],
[-1.9, 0.5],
[-1.5, 0.9],
[-0.9, 1.2],
[-1.1, 1.7],
[-1.4, 1.1]])
class3_points = np.array([[1.9, -1.2],
[1.5, -2.1],
[1.9, -0.5],
[1.5, -0.9],
[0.9, -1.2],
[1.1, -1.7],
[1.4, -1.1]])
class4_points = np.array([[-1.9, -1.2],
[-1.5, -2.1],
[-1.9, -0.5],
[-1.5, -0.9],
[-0.9, -1.2],
[-1.1, -1.7],
[-1.4, -1.1]])
#合并四类数据点
data = np.concatenate((class1_points,class2_points,class3_points,class4_points))
# 设置聚类数目
k = 2
# 迭代次数
max_iterations = 1000
# 从一维 数组 range(len(data)) 中选出 k个元素 replace=False同一个元素只能被选取一次
centroids = data[np.random.choice(range(len(data)),k,replace=False)]
#创建图形窗口
plt.figure()
#开始迭代
for a in range(max_iterations):
# 3、计算每个数据点与聚类中心的距离
distances = np.linalg.norm(data[:,np.newaxis,:]-centroids,axis=2)
# 4、更新聚类中心
# 分配每个数据点到最近的聚类中心
labels = np.argmin(distances,axis=1)
#更新新的中心
new_centroids = np.array([data[labels == i].mean(axis = 0) for i in range(k)])
plt.cla()
# 绘制连接线
for i in range(k):
cluster_points = data[labels == i]
centroid = centroids[i]
for cluster_point in cluster_points:
plt.plot([cluster_point[0], centroid[0]], [cluster_point[1], centroid[1]], 'k--')
# 绘制四类点,并分别用不同颜色标出来
plt.scatter(class1_points[:, 0], class1_points[:, 1], c="red")
plt.scatter(class2_points[:, 0], class2_points[:, 1], c="blue")
plt.scatter(class3_points[:, 0], class3_points[:, 1], c="cyan")
plt.scatter(class4_points[:, 0], class4_points[:, 1], c="green")
# 绘制聚类中心点,并用圆圈标记
plt.scatter(centroids[:, 0], centroids[:, 1], c="black", marker='o', s=100, label='Centroids')
plt.pause(1)
# 显示图形
# 如果新聚类中心与旧聚类中心相同,则收敛,结束迭代
# np.all判断给定轴向上的所有元素是否都为True
if np.all(centroids == new_centroids):
break
#更新聚类中心
centroids = new_centroids
plt.show()