一、设计原理
脉冲响应不变法是一种将模拟滤波器转换为数字滤波器的经典方法。其核心思想是通过对模拟滤波器的冲激响应进行等间隔采样来获得数字滤波器的单位脉冲响应。
设计步骤:
-
确定数字滤波器性能指标
-
将数字指标转换为等效的模拟滤波器指标
-
设计对应的模拟滤波器
-
将模拟滤波器转换为数字滤波器
二、MATLAB实现关键函数
-
butter(): 巴特沃斯滤波器设计 -
impinvar(): 脉冲响应不变法转换 -
freqz(): 数字滤波器频率响应分析 -
impz(): 数字滤波器脉冲响应分析
三、完整实现代码
%% IIR滤波器设计 - 脉冲响应不变法
clc; clear; close all;
% 设计参数
Fs = 1000; % 采样频率(Hz)
Fc = 100; % 截止频率(Hz)
N = 4; % 滤波器阶数
% 数字滤波器指标
Omega_c = 2*pi*Fc; % 模拟截止角频率(rad/s)
T = 1/Fs; % 采样间隔
% 设计模拟巴特沃斯滤波器
[bs, as] = butter(N, Omega_c, 's');
% 脉冲响应不变法转换
[bz, az] = impinvar(bs, as, Fs);
% 频率响应分析
figure;
freqz(bz, az, 1024, Fs);
title('数字滤波器频率响应');
% 脉冲响应对比
t = 0:T:0.1;
ha = impulse(tf(bs, as), t);
hd = impz(bz, az, length(t));
figure;
plot(t, ha, 'r', t, hd, 'b--');
legend('模拟滤波器','数字滤波器');
xlabel('时间(s)'); ylabel('幅度');
title('脉冲响应对比');
grid on;
% 幅频特性对比
[hs, ws] = freqs(bs, as, 1024);
[hz, wz] = freqz(bz, az, 1024);
figure;
subplot(2,1,1);
semilogx(ws/(2*pi), 20*log10(abs(hs)), 'r');
hold on;
semilogx(wz*Fs/(2*pi), 20*log10(abs(hz)), 'b');
xlabel('频率(Hz)'); ylabel('幅度(dB)');
title('幅频特性对比');
legend('模拟','数字');
axis([1 Fs/2 -100 5]);
grid on;
subplot(2,1,2);
semilogx(ws/(2*pi), unwrap(angle(hs)), 'r');
hold on;
semilogx(wz*Fs/(2*pi), unwrap(angle(hz)), 'b');
xlabel('频率(Hz)'); ylabel('相位(rad)');
title('相频特性对比');
grid on;
四、代码解析
-
参数设置:
-
采样频率Fs = 1000Hz
-
截止频率Fc = 100Hz
-
4阶巴特沃斯滤波器
-
-
设计流程:
-
先设计模拟巴特沃斯滤波器
-
使用impinvar函数进行数字转换
-
对比分析模拟/数字滤波器的频率响应和时域特性
-
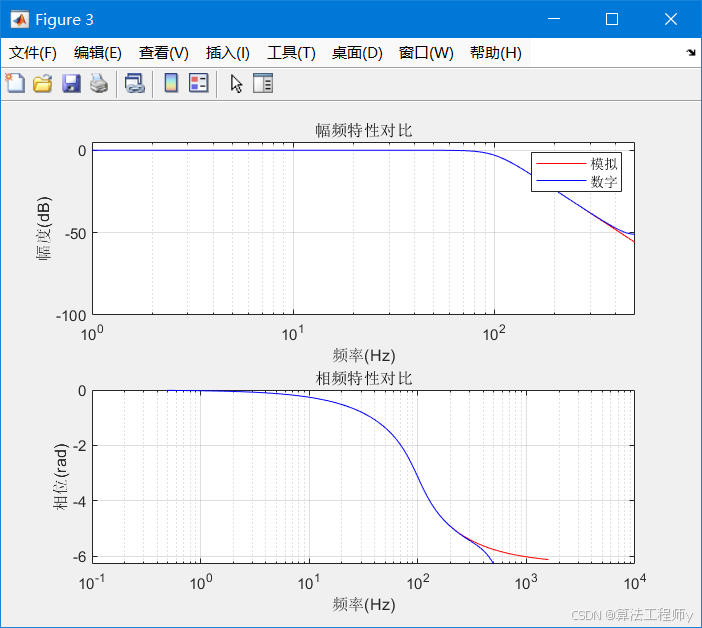
五、运行结果分析
-
频率响应:
-
数字滤波器在100Hz处呈现-3dB衰减
-
阻带衰减特性与模拟滤波器基本一致
-
高频段出现混叠效应(脉冲响应不变法固有特性)
-
-
时域特性:
-
数字滤波器脉冲响应与模拟滤波器采样值良好匹配
-
验证了脉冲响应不变法的时域等价性
-