2021年全国研究生数学建模竞赛华为杯

A题 相关矩阵组的低复杂度计算和存储建模

原题再现：

  一、问题背景
  计算机视觉、相控阵雷达、声呐、射电天文、无线通信等领域的信号通常呈现为矩阵的形式，这一系列的矩阵间通常在某些维度存在一定的关联性，因此数学上可用相关矩阵组表示。例如，视频信号中的单帧图像可视为一个矩阵，连续的多帧图像组成了相关矩阵组，而相邻图像帧或图像帧内像素间的关联性则反映在矩阵间的相关性上。随着成像传感器数量/雷达阵列/通信阵列的持续扩大，常规处理算法对计算和存储的需求成倍增长，从而对处理器件或算法的实现成本和功耗提出了巨大的挑战。因此，充分挖掘矩阵间关联性，以实现低复杂度的计算和存储，具有十分重要的价值和意义。
  二、建模描述



  下面对建模过程中涉及的计算复杂度、存储复杂度的定义进行说明：
  计算复杂度定义为由矩阵组H计算得到结果矩阵组W所需要的总计算复杂度。复数矩阵运算可拆解为基本的复数运算，而基本的复数运算又可进一步拆解为基本的实数运算。例如，复数乘法按照(a+bj)(c+dj)=(ac-bd)+(ad+bc)j计算的复杂度为4次实数乘法和2次实数加(减)法。实数基本运算的复杂度按照下表计算，其中，实数的加(减)法运算与乘法运算的计算复杂度对比可参考文献[1]。





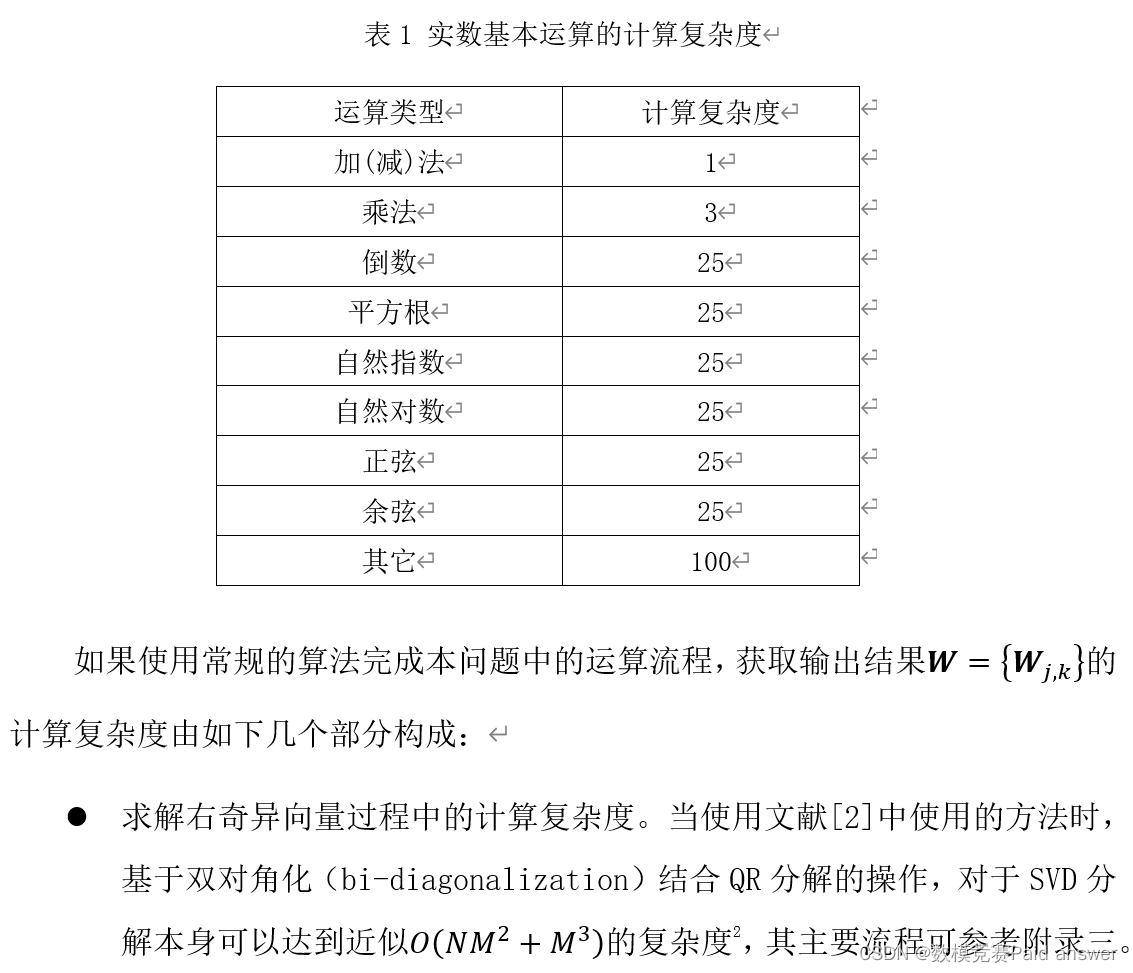
  三、建模问题
  输入矩阵组𝑯、标准中间矩阵组𝑽和标准输出矩阵组𝑾的数据及其维度如下，数据采用十进制格式：

  附件中提供.mat 及.csv 文件格式的数据，按需使用其中的一种文件格式即可。
  请基于以上提供的数据，采用适当的方法，解决以下相关矩阵组的低复杂度计算和存储建模问题。注意，提交结果及论文需要完成以下问题 1、问题 2 中的至少一题，同时完成两题将适当加分。问题 3 为开放式问题，不作为必选，但鼓励尝试，有新意的算法模型设计将得到加分。
  在完成以下问题时，仅需考虑各个问题本身申明的建模需求，不需要考虑其他问题产生的建模需求。例如，在完成问题 3 时，不需要额外考虑问题 1 中𝜌min(𝑉)的建模估计精度需求。
  问题 1：相关矩阵组的低复杂度计算

  问题 2：相关矩阵组的低复杂度存储
  基于给定的所有矩阵数据𝑯和𝑾，分析各自数据间的关联性，分别设计相应的压缩𝑃1(∙)、𝑃2(∙)和解压缩𝐺1(∙)、𝐺2(∙)模型，在满足误差𝑒𝑟𝑟𝑯 ≤ 𝐸𝑡ℎ1 = −30dB、𝑒𝑟𝑟𝑾 ≤ 𝐸𝑡ℎ2 = −30dB的情况下，使得存储复杂度和压缩与解压缩的计算复杂度最低，复杂度计算同问题 1。
  ⚫ 注 1：压缩与解压缩函数的设计方法不做限定。
  ⚫ 注 2：计算复杂度考虑压缩和解压缩函数的所有运算过程。
  ⚫ 注 3：在本问题中，暂不考虑分析模型𝑾̂ = 𝑓(𝑯)对输出矩阵组𝑾的影
响。
  ⚫ 注 4：两个建模优化目标（存储复杂度，压缩与解压缩的计算复杂度）的优先级相同。
  问题 3：相关矩阵组的低复杂度计算和存储
  基于给定的所有矩阵数据𝑯，分析其数据间的关联性，在满足𝜌min(𝑾) ≥𝜌𝑡ℎ = 0.99的情况下，设计低复杂度计算和存储的整体方案，完成从矩阵输入信号𝑯到近似矩阵输出信号𝑾̂的端到端流程。
  ⚫ 注 1：在本问题中，可以考虑从矩阵输入信号𝑯到近似矩阵输出信号𝑾̂为一个整体流程，而非依次经过“压缩/解压缩、计算单元、压缩/解压缩”的过程。
  ⚫ 注 2：如果使用人工智能方法，需要考虑人工智能模型的存储复杂度以及推理阶段的计算复杂度。

整体求解过程概述(摘要)

  相关矩阵组在无线通信、雷达、图像/视频处理等领域都有广泛的应用，其特点在于数据之间具有较强的相关性。数据维数的不断增长，使得充分挖掘矩阵间关联性以实现低复杂度的计算和存储具有十分重要的价值和意义。
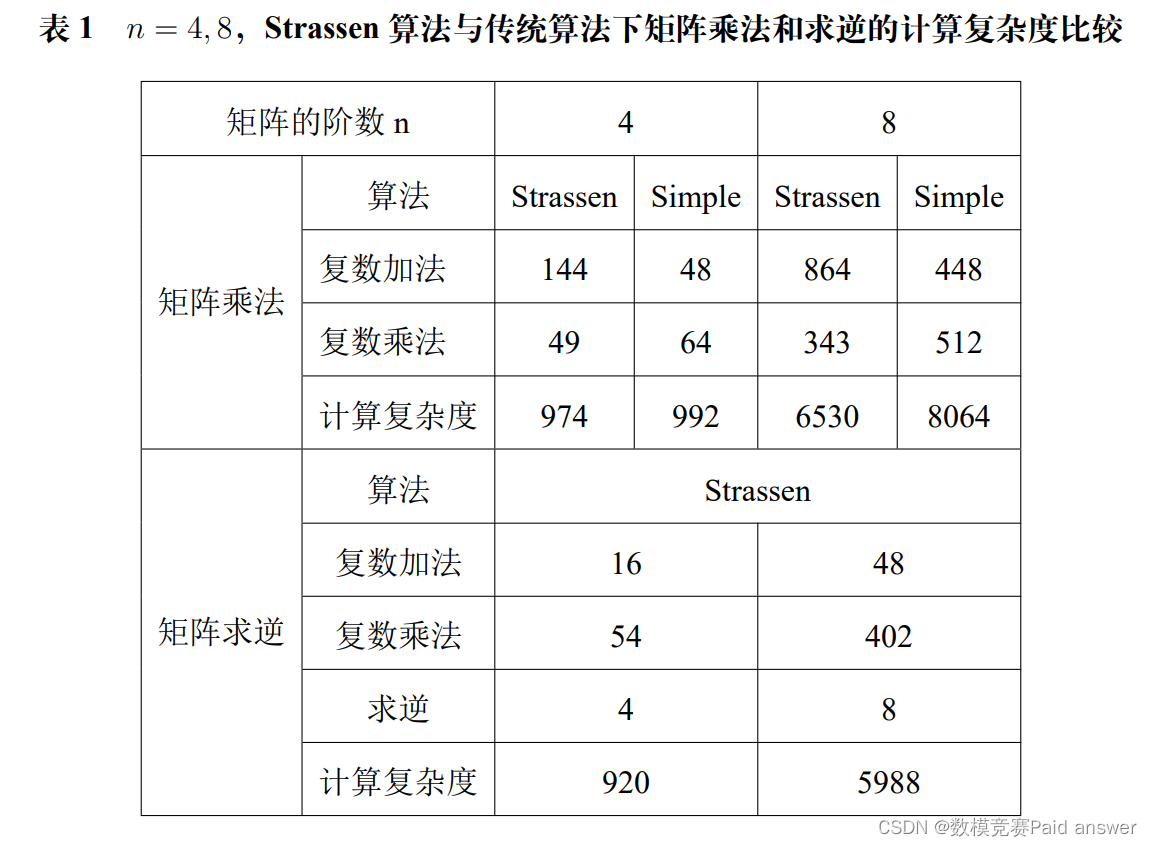
  对于问题一，本文从每个子矩阵的自相关性出发，基于随机 SVD 分解方法对目标矩阵降维，并使用基于双对角化和 QR 分解的 SVD 分解计算 V。之后本文基于 AOR 迭代算法，从子矩阵自身的相关性出发，训练出合适的迭代因子，使得计算 W 时矩阵求逆的迭代次数大大减少。基于 Strassen 算法，对算法中涉及的矩阵运算进行分治计算，从而进一步降低计算复杂度。最后，本文从矩阵行块间的相关性出发，构建相邻子矩阵的互相关函数模型，建立互相关函数与插值算法的关系，给出最优插值系数。在矩阵 V 和矩阵 W 的计算中，理论上可以减少约 40% 的计算量。
  对于问题二，本文提出一种基于 SVD 分解的相关矩阵组压缩算法，通过对矩阵重新排列、合并、SVD 分解并提取最大奇异值对应的列向量，可以实现对矩阵组数据的有效压缩。本文基于 SVD 分解对矩阵间相关性进行分析，验证了该压缩/解压缩算法的可行性。本文进一步推导对这种方法的存储复杂度、压缩复杂度以及解压复杂度，并建立多目标优化模型，求解最优的压缩参数。最优解的压缩率可达 0.3867，且具有较低的压缩、解压复杂度。
  对于问题三，本文提出了一种联合优化策略，将问题一的中间变量存储复杂度和插值存储复杂度纳入到优化方案当中进行讨论。同时我们将迭代算法的结构调整为逐元素运算的形式，避免了部分矩阵存储的复杂度。

模型假设：

  • 对于同一数据集的同一行块中的矩阵满足相同分布，具有相同的统计特性；
  • 不同数据集之间、同一数据集不同行块之间的分布彼此独立；
  • 同一个行块内的矩阵之间具有相关性，且矩阵间的距离越近，其相关性越强。

模型的建立与求解

子问题 1——矩阵 V 的近似低复杂度计算

基于随机 SVD 算法的目标矩阵降维

  QR 分解可将矩阵 A 分解为一个正交矩阵 Q 和一个上三角矩阵 R 的乘积。经典的 QR 矩阵分解方法主要有 Gram–Schmidt 方法、Householder 反射方法和Givens 旋转方法三种。考虑到需要计算的矩阵维数并不大，且后两种方法都需要计算反三角函数，会导致计算量较大。故这里采用第一种方法。基于 Gram–Schmidt 正交化方法的 QR 分解算法如下。

  由于经典的 Gram–Schmidt 正交化方法对舍入误差很敏感，容易导致生成的基 qj 的正交性随着迭代越来越弱，因此这里使用改进的 Gram–Schmidt 正交化方法, 其核心思想是，在每个 qj 生成后，直接把 A 剩下的列都去掉 qj 的成分。它与传统方法的区别仅仅是把计算的顺序变了，但是改进之后稳定性会好很多。

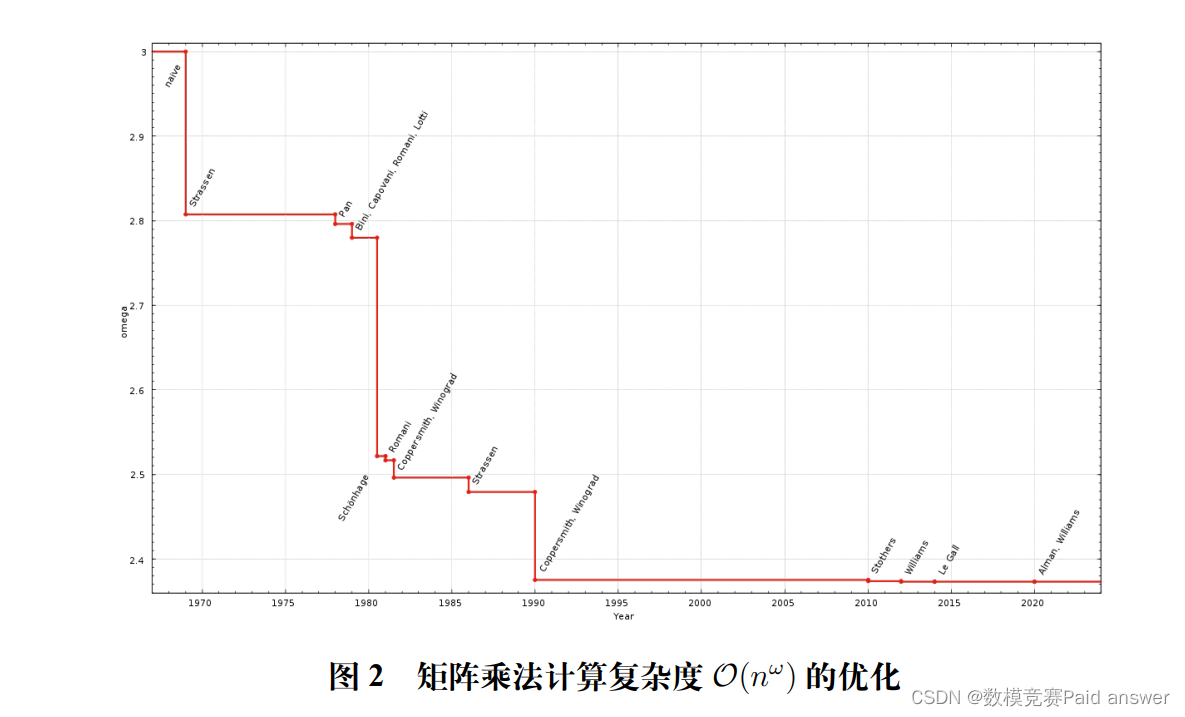
基于分治思想的矩阵低复杂度计算

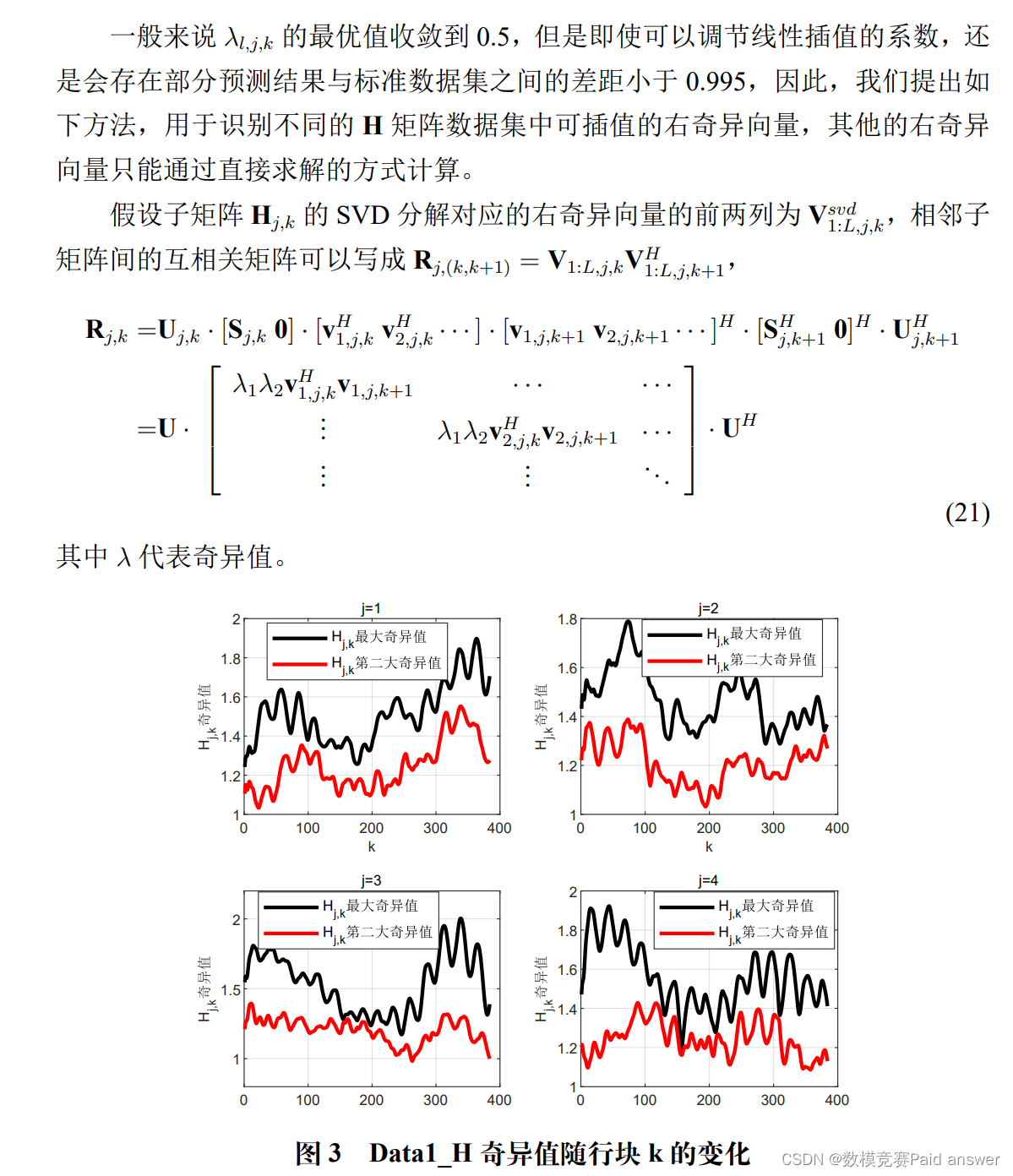
右奇异向量相关性分析

  通过对数据集中的子矩阵进行简单分析，我们可以发现，这些子矩阵的奇异值随着行块数周期性波动，因此我们推测，行子矩阵之间的相关性可以用奇异值或者特征值之间的函数关系加以刻画，矩阵的 SVD 分解将矩阵的相关信息集中到对角线上的奇异值上，右奇异向量中继承了矩阵 H 的部分相关性和随机性。

基于 SVD 分解的压缩和解压缩

function [comp,loopcount,err_H] = HC(H,M,N,J,K,snap,cut,thre)
%compression
comp = cell(J,ceil(K/snap));
loopcount = zeros(J,ceil(K/snap));
for j = 1:J
X = zeros(M*N,snap);
count = 0;kk = 0;
for k = 1:K
HH = H(:,:,j,k);
kk = kk + 1;
X(:,kk) = reshape(HH,[M*N 1]);
if kk==snap || k == K
count = count + 1;
[U,S,V,lc] = svdsim(X,thre);
%[U,S,V] = svd(X);
comp{j,count}.U = U(:,1:cut);
comp{j,count}.S = diag(S(1:cut,1:cut));
comp{j,count}.V = V(:,1:cut);
loopcount(j,count) = lc;
kk = 0;
end
end
end
%decompression
H_hat = zeros(size(H));
for j = 1:J
for count = 1:size(comp,2)
X_re = comp{j,count}.U * diag(comp{j,count}.S) *
comp{j,count}.V';
for kk = 1:snap
H_hat(:,:,j,(count-1)*snap+kk) = reshape(X_re(:,kk),[M N]);
end
end
end
%entropy calculation
E = zeros(J,K);
F = zeros(J,K);
for j = 1:J
for k = 1:K
HH = H(:,:,j,k);
H_re = H_hat(:,:,j,k);
E(j,k) = norm(H_re-HH,'fro')^2;
F(j,k) = norm(HH,'fro')^2;
end
end
err_H = 10*log10(mean(E,'all')/mean(F,'all'));
end

论文缩略图：

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

基于随机 SVD 分解的矩阵降维

function [V,rho_V_err,Q,V_real,B,loopcount] = random_svd(A,iter)
%% calculate Q
[m,n]=size(A);
Q=[];
L=2;
for t=1:iter
w=(randn(n,1)+1j*randn(n,1))*sqrt(0.5)*0.01;
y=A*w;
if t==1
q=eye(m)*y;
else
q=(eye(m)-Q*Q')*y;
end
q_norm=norm(q,2);
qn=q./q_norm;
Q=[Q qn];
end
%% B=QA SVD
B=Q'*A;
[U,~,~,loopcount] = svdsim(B,0.001);
[~,~,V_real]=svds(A',2);
QU=Q*U;
V=QU(:,1:2);
rho_V_err=zeros(L,1);
for l=1:L
Vl=V(:,l);
V_reall=V_real(:,l);
rho_V_err(l)= norm(Vl'*V_reall)/norm(Vl)/norm(V_reall);
end
end

基于 QR 分解和双对角化的 SVD 分解

function [u,s,v,loopcount] = svdsim(a,tol)
if ~exist('tol','var')
tol=eps*1024;
end
%reserve space in advance
sizea=size(a);
loopmax=100*max(sizea);
loopcount=0;
% or use Bidiag(A) to initialize U, S, and V
u=eye(sizea(1));
s=a';
v=eye(sizea(2));
Err=realmax;
while Err>tol && loopcount<loopmax
% log10([Err tol loopcount loopmax]); pause
[q,s]=qr(s'); u=u*q;
[q,s]=qr(s'); v=v*q;
% exit when we get "close"
e=triu(s,1);
E=norm(e(:));
F=norm(diag(s));
if F==0, F=1;end
Err=E/F;
loopcount=loopcount+1;
end
% [Err/tol loopcount/loopmax]
%fix the signs in S
ss=diag(s);
s=zeros(sizea);
for n=1:length(ss)
ssn=ss(n);
s(n,n)=abs(ssn);
if ssn<0
u(:,n)=-u(:,n);
end
end
if nargout<=1
u=diag(s);
end
return

AOR 迭代算法

function x = AOR(A,y,k,w,r)
E=-tril(A,-1);
F=-triu(A,1);
D=diag(diag(A));
U=inv(D-r*E);
N2=(1-w)*D+(w-r)*E+w*F;
x=1/1.01*y;
for i=1:size(y,2)
for j=1:k
x(:,i)=U*N2*x(:,i)+w*U*y(:,i);
end
end
end

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可