[NOIP2018 普及组] 龙虎斗

通往洛谷的传送门

题目背景

NOIP2018 普及组 T2

题目描述

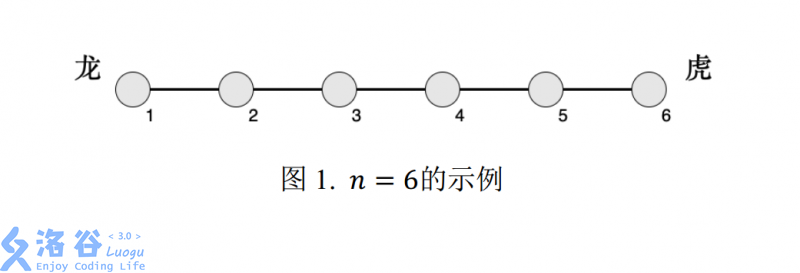
轩轩和凯凯正在玩一款叫《龙虎斗》的游戏，游戏的棋盘是一条线段，线段上有 $n$ 个兵营（自左至右编号 $1\sim n$），相邻编号的兵营之间相隔 $1$ 厘米，即棋盘为长度为 $n-1$ 厘米的线段。$i$ 号兵营里有 $c_i$ 位工兵。下面图 1 为 $n=6$ 的示例：

轩轩在左侧，代表“龙”；凯凯在右侧，代表“虎”。 他们以 $m$ 号兵营作为分界， 靠左的工兵属于龙势力，靠右的工兵属于虎势力，而第 $m$ 号兵营中的工兵很纠结，他们不属于任何一方。

一个兵营的气势为：该兵营中的工兵数$ \times $ 该兵营到 $m$ 号兵营的距离；参与游戏 一方的势力定义为：属于这一方所有兵营的气势之和。
下面图 2 为 $n=6,m=4$ 的示例，其中红色为龙方，黄色为虎方：

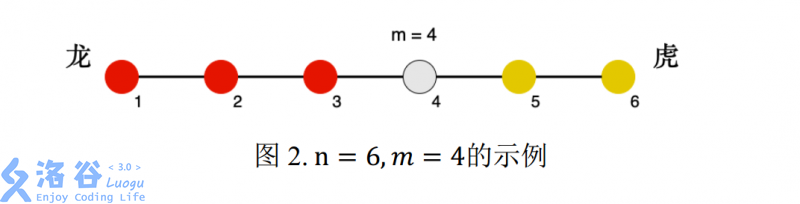
游戏过程中，某一刻天降神兵，共有 $s_1$ 位工兵突然出现在了 $p_1$ 号兵营。作为轩轩和凯凯的朋友，你知道如果龙虎双方气势差距太悬殊，轩轩和凯凯就不愿意继续玩下去了。为了让游戏继续，你需要选择一个兵营 $p_2$，并将你手里的 $s_2$ 位工兵全部派往 兵营 $p_2$，使得双方气势差距尽可能小。

注意：你手中的工兵落在哪个兵营，就和该兵营中其他工兵有相同的势力归属（如果落在 $m$ 号兵营，则不属于任何势力）。

输入格式

输入文件的第一行包含一个正整数$n$，代表兵营的数量。

接下来的一行包含 $n$ 个正整数，相邻两数之间以一个空格分隔，第 $i$ 个正整数代 表编号为 $i$ 的兵营中起始时的工兵数量 $c_i$。

接下来的一行包含四个正整数，相邻两数间以一个空格分隔，分别代表 $m,p_1,s_1,s_2$。

输出格式

输出文件有一行，包含一个正整数，即 $p_2$，表示你选择的兵营编号。如果存在多个编号同时满足最优，取最小的编号。

输入输出样例

输入 #1

6 
2 3 2 3 2 3 
4 6 5 2

输出 #1

2

输入 #2

6 
1 1 1 1 1 16 
5 4 1 1

输出 #2

1

提示

样例 1 说明

见问题描述中的图 2。
双方以 $m=4$ 号兵营分界，有 $s_1=5$ 位工兵突然出现在 $p_1=6$ 号兵营。
龙方的气势为：
$$2\times (4-1)+3\times (4-2)+2\times (4-3)=14$$
虎方的气势为：
$$2\times (5-4)+(3+5)\times (6-4)=18$$
当你将手中的 $s_2=2$ 位工兵派往 $p_2=2$ 号兵营时，龙方的气势变为：
$$14+2\times (4-2)=18$$
此时双方气势相等。

样例 2 说明

双方以 $m=5$ 号兵营分界，有 $s_1=1$ 位工兵突然出现在 $p_1=4$ 号兵营。
龙方的气势为：
$$1\times (5-1)+1\times (5-2)+1\times (5-3)+(1+1)\times (5-4)=11$$
虎方的气势为：
$$16\times (6-5)=16$$
当你将手中的 $s_2=1$ 位工兵派往 $p_2=1$ 号兵营时，龙方的气势变为：
$$11+1\times (5-1)=15$$
此时可以使双方气势的差距最小。

数据规模与约定

$1<m<n$，$1\le p_1\le n$。
对于 $20\%$ 的数据，$n=3,m=2,c_i=1,s_1,s_2\le 100$。
另有 $20\%$ 的数据，$n\le 10,p_1=m,c_i=1,s_1,s_2\le 100$。
对于 $60\%$ 的数据，$n\le 100,c_i=1,s_1,s_2\le 100$。
对于 $80\%$ 的数据，$n\le 100,c_i,s_1,s_2\le 100$。
对于 $100\%$ 的数据，$n\le 10^5$,$c_i,s_1,s_2\le 10^9$。

1.思路解析

    建立双重循环，第一层枚举$p_2$名士兵的去向。第二层分别枚举计算龙的气势和虎的气势。如下：

    注意上面的数据量：$c_i,s_1,s_2\le 10^9$，很明显要开long long。

#include<bits/stdc++.h>
using namespace std;
//用minnum储存最小气势差,dragon储存当前龙的气势,tiger储存当前虎的气势 
long long n,c[100010],m,p1,s1,s2,p2=1,minnum=LONG_LONG_MAX,dragon,tiger;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)cin>>c[i];
    cin>>m>>p1>>s1>>s2;
    c[p1]+=s1;
    for(int i=1;i<=n;i++)//枚举p2
    {
        dragon=tiger=0;
        for(int j=1;j<m;j++)dragon+=(m-j)*c[j];//预处理龙的气势 
        for(int j=m+1;j<=n;j++)tiger+=(j-m)*c[j];//预处理虎的气势
    	if(i<m)dragon+=(m-i)*s2;//为虎加上气势 
    	else if(i>m)tiger+=(i-m)*s2;//为龙加上气势 
    	if(abs(dragon-tiger)<minnum)//更新最小值 
    	{
    		minnum=abs(dragon-tiger);
    		p2=i;
		}
		if(i<m)dragon-=(m-i)*s2;//回溯 
    	else if(i>m)tiger-=(i-m)*s2;
	}
	cout<<p2;
    return 0;
}

    但是通过估算，$O(N^2)$的复杂度通过不了$10^5$的数据量。现实也确实如此。

    我们发现，不需要每一次都额外计算一次气势。在开始的时候预处理，只需要在后面计算增量就行了。不过多阐述，详见代码。

2.AC代码

#include<bits/stdc++.h>
using namespace std;
//用minnum储存最小气势差,dragon储存当前龙的气势,tiger储存当前虎的气势 
long long n,c[100010],m,p1,s1,s2,p2=1,minnum=LONG_LONG_MAX,dragon,tiger;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)cin>>c[i];
    cin>>m>>p1>>s1>>s2;
    c[p1]+=s1;
    for(int i=1;i<m;i++)dragon+=(m-i)*c[i];//预处理龙的气势 
    for(int i=m+1;i<=n;i++)tiger+=(i-m)*c[i];//预处理虎的气势
    for(int i=1;i<=n;i++)//枚举p2 
    {
    	if(i<m)dragon+=(m-i)*s2;//为虎加上气势 
    	else if(i>m)tiger+=(i-m)*s2;//为龙加上气势 
    	if(abs(dragon-tiger)<minnum)//更新最小值 
    	{
    		minnum=abs(dragon-tiger);
    		p2=i;
		}
		if(i<m)dragon-=(m-i)*s2;//回溯 
    	else if(i>m)tiger-=(i-m)*s2;
	}
	cout<<p2;
    return 0;
}