无论何时何地,我都认为对于一道编程题,思考解法的时间用于是实际动手解决问题的2倍!如果敲键盘编码需要5min,那么思考解法的过程至少就需要10分钟。
1. 题目

2. 思想
其实这就是一道模拟题,难度中等。做这种题的关键就是需要:先把边界情况搞清楚,然后自己手动模拟一下是否能够正确输出。在这个基础上,再写代码。一定是先思考,思考清楚后,再动手编码。
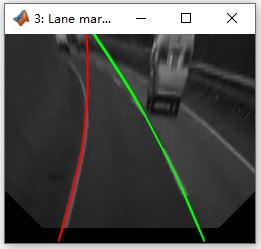
知道这题是一道模拟题,那么该怎么写呢?观察图片,有如下几个特征:
(1)运动轨迹不是斜向往上,就是斜向往下。斜向向上的过程中典型的就是i=i-1,j=j+1;
(2)但是运动到什么时候就改变了运动轨迹了呢?这个地方需要分类讨论。
- 运动轨迹是斜向上的时候:要么是i当前的值是0(表示是第一行,没法再往上了),要么是j的值是m-1(表示是最后一列,也没法再往上了)
- 运动轨迹是斜向下的时候:要么是j的值为0(表示是第一列,没法再往下了),要么是i的值是n-1(表示是最后一行,也没法再往下了)
在上述这两类下,需要改变运动轨迹。
(3)但是还有一个问题,就是运动轨迹改变后,那么就需要同步修改一下坐标的位置了。这里我们可以设置一个change变量,用于判断是否需要变换位置。change的作用是在如下绿色指针的地方:

把上面三个特征进行编码,那么这题就解决了80%的问题了,还剩一部分细节需要处理。
剩下的细节是什么呢?也就是对应下面这个红框中的内容:
j=j+1的前提是j!=m-1i=i+1的前提是i!=n-1

3. 代码
class Solution:
def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
cnt = 0
res = []
i = 0
j = 0
up = 1 # 向上的标志
n = len(mat)
m = len(mat[0])# 列
while(cnt < m*n):
print(i,j, mat[i][j],", up = ", up)
res.append(mat[i][j])
# 判断接下来的方向
if (up == 1 and i == 0) or (up == 1 and j == m-1):
print("here,", i, j)
change = 1
if (up == 0 and j == 0) or (up == 0 and i == n-1):
change = 1
# 下一步的位置是特殊变动还是按照up来变动?
if change: # 特殊变动
# print("in change", i, j , "up=",up)
if up == 1 and i == 0 and j!= m-1:
j = j + 1
up = 0
elif up == 1 and j == m-1:
# print("here")
i = i + 1
up = 0
elif up == 0 and j == 0 and i != n-1:
i = i + 1
up = 1
elif up == 0 and i == n-1:
j = j + 1
up = 1
change = 0
else: # 按照up变动
# 如果是向上
if up:
i = i - 1
j = j + 1
else:
i = i + 1
j = j - 1
# 切换up
cnt += 1
print(res)
return res