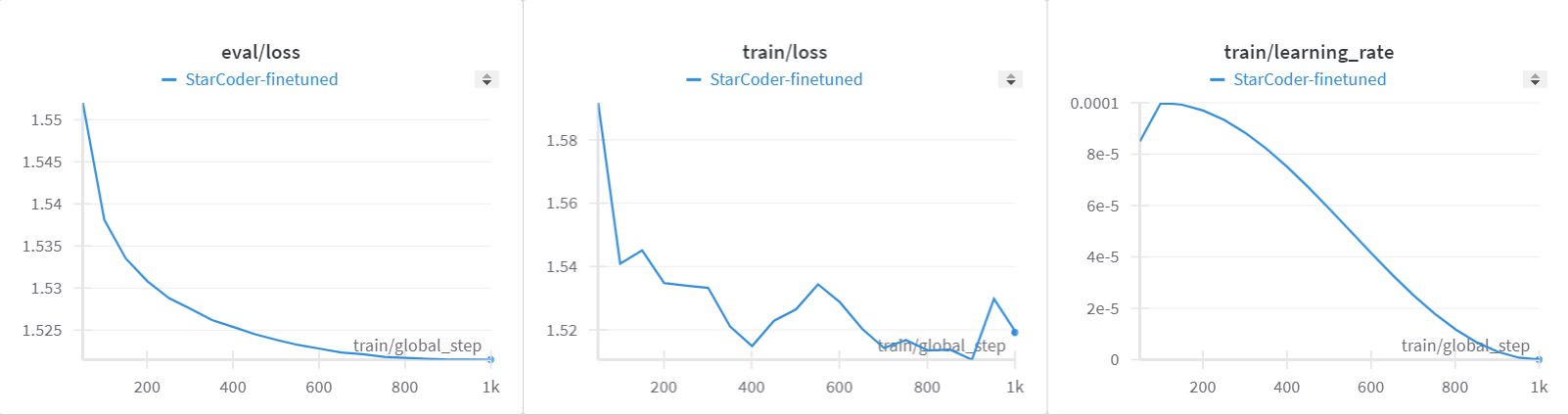
目录
- T1
T1
设
{
O
;
e
1
,
e
2
,
e
3
}
\{O;e_1,e_2,e_3\}
{O;e1,e2,e3} 是一个正交标架
,
σ
,\sigma
,σ 是
{
1
,
2
,
3
}
\{1,2,3\}
{1,2,3} 的一个置换,证明:
(1)
{
O
;
e
σ
(
1
)
,
e
σ
(
2
)
,
e
σ
(
3
)
}
\{ O; e_{\sigma ( 1) }, e_{\sigma ( 2) }, e_{\sigma ( 3) }\}
{O;eσ(1),eσ(2),eσ(3)} 是一个正交标架;
(
2
)
{
O
;
e
1
,
e
2
,
e
3
}
(2)\left\{O;e_1,e_2,e_3\right\}
(2){O;e1,e2,e3}与
{
O
;
e
σ
(
1
)
,
e
σ
(
2
)
,
e
σ
(
3
)
}
\left\{O;e_\sigma(1),e_{\sigma(2)},e_{\sigma(3)}\right\}
{O;eσ(1),eσ(2),eσ(3)}定向相同当且仅当
σ
\sigma
σ是偶置换.
证明:
(1) 由于
{
O
;
e
1
,
e
2
,
e
3
}
\left\{O;e_1,e_2,e_3\right\}
{O;e1,e2,e3}是正交标架,当
i
≠
j
i\neq j
i=j 时
,
σ
(
i
)
≠
σ
(
j
)
,\sigma(i)\neq\sigma(j)
,σ(i)=σ(j),故
⟨
e
σ
(
i
)
,
e
σ
(
j
)
⟩
=
\left\langle\mathbf{e}_\sigma(i),\mathbf{e}_{\sigma(j)}\right\rangle=
⟨eσ(i),eσ(j)⟩= 0;当
i
=
j
i=j
i=j时
,
σ
(
i
)
=
σ
(
j
)
,\sigma(i)=\sigma(j)
,σ(i)=σ(j),故
⟨
e
σ
(
i
)
,
e
σ
(
j
)
⟩
=
1.
\langle\mathbf{e}_\sigma(i),\mathbf{e}_{\sigma(j)}\rangle=1.
⟨eσ(i),eσ(j)⟩=1.因此
,
{
O
;
e
σ
(
1
)
,
e
σ
(
2
)
,
e
σ
(
3
)
}
,\{O;e_\sigma(1),e_{\sigma(2)},e_{\sigma(3)}\}
,{O;eσ(1),eσ(2),eσ(3)}是一个正交标架.
(
2
)
{
O
;
e
1
,
e
2
,
e
3
}
(2)\left\{O;e_{1},e_{2},e_{3}\right\}
(2){O;e1,e2,e3}与
{
O
;
e
σ
(
1
)
,
e
σ
(
2
)
,
e
σ
(
3
)
}
\left\{O;e_\sigma(1),e_{\sigma(2)},e_{\sigma(3)}\right\}
{O;eσ(1),eσ(2),eσ(3)}定向相同
⇔
1
=
(
e
σ
(
1
)
,
e
σ
(
2
)
,
e
σ
(
3
)
)
=
\Leftrightarrow1=(e_\sigma(1),e_{\sigma(2)},e_{\sigma(3)})=
⇔1=(eσ(1),eσ(2),eσ(3))=
(
−
1
)
∣
σ
∣
⇔
∣
σ
∣
(-1)^{|\sigma|}\Leftrightarrow|\sigma|
(−1)∣σ∣⇔∣σ∣是偶数
⇔
σ
\Leftrightarrow\sigma
⇔σ是偶置换,其中
∣
σ
∣
|\sigma|
∣σ∣是置换
σ
\sigma
σ的长度.