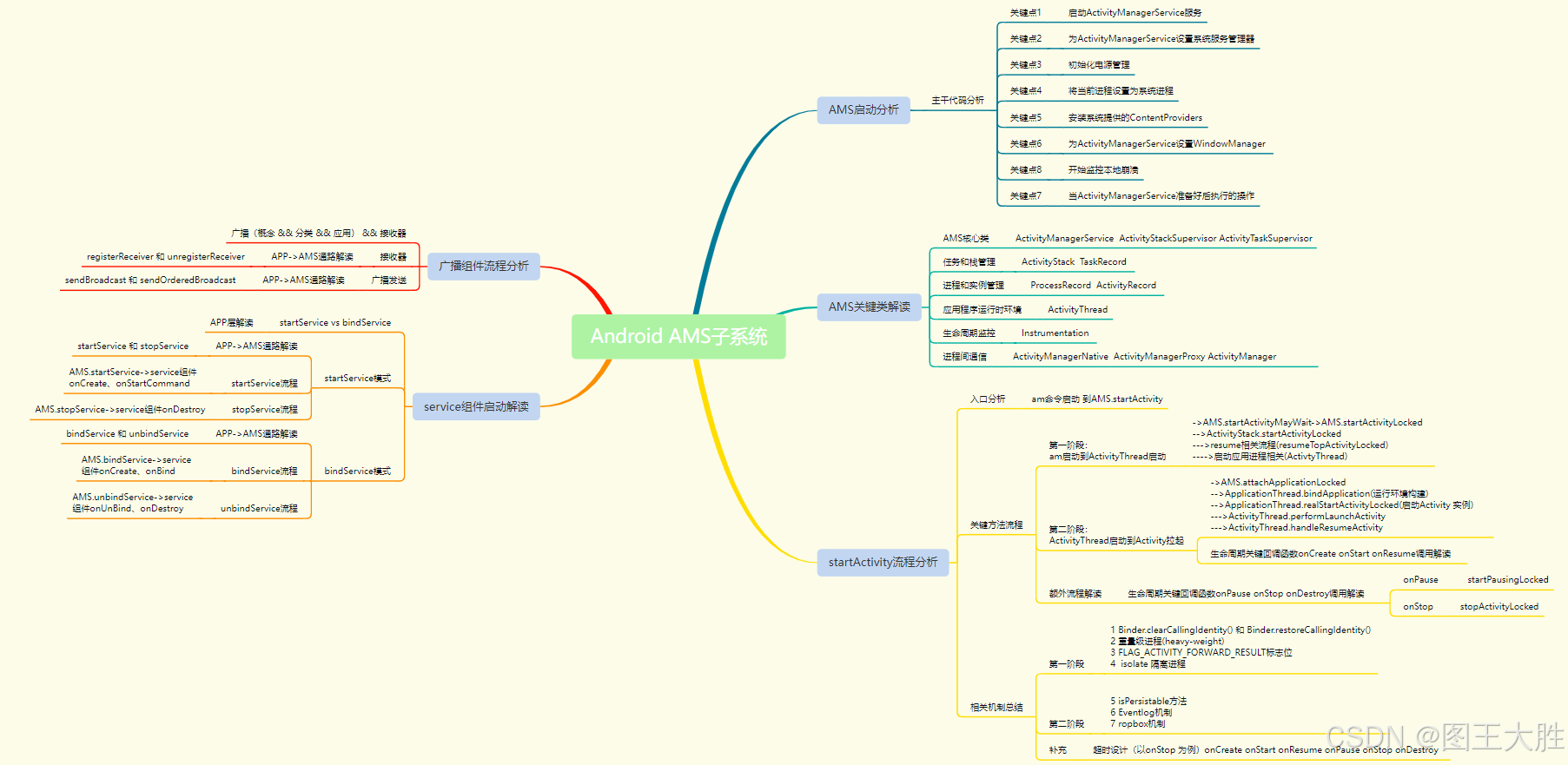
给定两棵树 T1 和 T2。如果 T1 可以通过若干次左右孩子互换就变成 T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。

图一

图二
现给定两棵树,请你判断它们是否是同构的。
输入格式:
输入给出2棵二叉树的信息。对于每棵树,首先在一行中给出一个非负整数 n (≤10),即该树的结点数(此时假设结点从 0 到 n−1 编号);随后 n 行,第 i 行对应编号第 i 个结点,给出该结点中存储的 1 个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出 “-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的,输出“Yes”,否则输出“No”。
输入样例1(对应图1):
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
输出样例1:
Yes
输入样例2(对应图2):
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
输出样例2:
No
- 对于每棵树,其节点的数量、层次结构和连接关系必须完全一致。
- 如果树上的节点带有特定的标签或值,则这些标签也必须一一对应相等。
既然判断树的同构,那我们就应该先构建一个树形结构:
typedef struct tree
{
char data; // 节点数据
int left; // 左子节点索引
int right; // 右子节点索引
} tree;
- 声明了两个全局数组
T1和T2,以及一个检查数组check,用于存储两棵树的节点信息和标记哪些节点已经被访问过。
// 全局数组用于存放两个树的节点信息
tree T1[MAXTREE], T2[MAXTREE];
// 检查数组,用于标记已访问过的节点
int check[MAXTREE];
构建树的函数 (
buildTree()):
- 接受一个指向
tree结构体数组的指针参数t,用于接收用户输入并构建树。- 用户需要输入节点总数,然后依次输入每个节点的数据及其左右孩子的索引。
- 函数通过遍历输入的节点信息,填充
tree结构体数组,并找到根节点的索引后返回。判断两棵树是否同构的函数 (
Isomorphism()):
- 这是一个递归函数,接受两个参数,分别为两棵树的根节点索引。
- 通过对比两棵树的各个节点数据和子节点结构,确定它们是否同构。
// 构建树的函数
int buildTree(tree* t);
// 判断两棵树是否同构的递归函数
int Isomorphism(int root1, int root2);主函数调用buildTree函数构建树形结构
int main()
{
int r1, r2;
// 分别构建两棵树
r1 = buildTree(T1);
r2 = buildTree(T2);
// 如果两棵树同构,打印"Yes"
if (Isomorphism(r1, r2))
{
printf("Yes\n");
}
// 否则打印"No"
else
{
printf("No\n");
}
return 0;
}构建树的函数
int buildTree(tree* t)
{
int root = null, i;
int n;
char cleft, cright;
// 输入节点数量
scanf("%d", &n);
// 如果节点数量大于零
if (n > 0)
{
// 初始化检查数组
memset(check, 0, sizeof(check));
// 遍历所有节点,输入节点数据及左右子节点索引
for (i = 0; i < n; i++)
{
// 忽略换行符
getchar();
// 输入当前节点的数据及左右子节点索引
scanf("%c %c %c", &t[i].data, &cleft, &cright);
// 处理左子节点
if (cleft!= '-')
{
t[i].left = cleft - '0'; // 将字符形式的索引转为整数
check[t[i].left] = 1; // 标记此子节点已被访问
}
else
t[i].left = null; // 空节点
// 处理右子节点
if (cright!= '-')
{
t[i].right = cright - '0'; // 将字符形式的索引转为整数
check[t[i].right] = 1; // 标记此子节点已被访问
}
else
{
t[i].right = null; // 空节点
}
}
// 找到根节点
for (i = 0; i < n; i++)
{
//没有被访问过
if (!check[i])
{
break;
}
}
// 返回根节点索引
root = i;
}
// 返回根节点索引
return root;
}memset(check, 0, sizeof(check)); :
这里使用memset函数清空check数组,准备记录哪些节点已经被访问过。
下面是判断两棵树是否同构的算法:
int Isomorphism(int root1, int root2)
{
// 如果两个根节点都为空,返回真
if (root1 == null && root2 == null)
{
return 1;
}
// 如果两个根节点不都为空
else
{
// 如果只有一个根节点为空,返回假
if (root1 == null && root2!= null || root1!= null && root2 == null)
{
return 0;
}
else
{
// 如果两个根节点都不为空且数据不同,返回假
if (T1[root1].data!= T2[root2].data)
{
return 0;
}
// 如果两个根节点数据相同,继续比较子节点
else
{
// 如果两个根节点都没有左子节点,只比较右子节点
if (T1[root1].left == null && T2[root2].left == null)
{
return Isomorphism(T1[root1].right, T2[root2].right);
}
// 如果两个根节点都有左子节点且数据相同,分别比较左右子节点
else
{
if (T1[root1].left!= null && T2[root2].left!= null && T1[T1[root1].left].data == T2[T2[root2].left].data)
{
return Isomorphism(T1[root1].left, T2[root2].left) && Isomorphism(T1[root1].right, T2[root2].right);
}
// 如果两个根节点都有左子节点但数据不同,交换左右子节点进行比较
else
{
return Isomorphism(T1[root1].right, T2[root2].left) && Isomorphism(T1[root1].left, T2[root2].right);
}
}
}
}
}
}完整代码附上:
#include <stdio.h>
#include <string.h>
// 定义最大树的大小
#define MAXTREE 10
// 定义空节点的标识
#define null -1
// 树结构体
typedef struct tree
{
char data; // 节点数据
int left; // 左子节点索引
int right; // 右子节点索引
} tree;
// 全局数组用于存放两个树的节点信息
tree T1[MAXTREE], T2[MAXTREE];
// 检查数组,用于标记已访问过的节点
int check[MAXTREE];
// 构建树的函数
int buildTree(tree* t);
// 判断两棵树是否同构的递归函数
int Isomorphism(int root1, int root2);
int main()
{
int r1, r2;
// 分别构建两棵树
r1 = buildTree(T1);
r2 = buildTree(T2);
// 如果两棵树同构,打印"Yes"
if (Isomorphism(r1, r2))
{
printf("Yes\n");
}
// 否则打印"No"
else
{
printf("No\n");
}
return 0;
}
// 构建树的函数实现
int buildTree(tree* t)
{
int root = null, i;
int n;
char cleft, cright;
// 输入节点数量
scanf("%d", &n);
// 如果节点数量大于零
if (n > 0)
{
// 初始化检查数组
memset(check, 0, sizeof(check));
// 遍历所有节点,输入节点数据及左右子节点索引
for (i = 0; i < n; i++)
{
// 忽略换行符
getchar();
// 输入当前节点的数据及左右子节点索引
scanf("%c %c %c", &t[i].data, &cleft, &cright);
// 处理左子节点
if (cleft!= '-')
{
t[i].left = cleft - '0'; // 将字符形式的索引转为整数
check[t[i].left] = 1; // 标记此子节点已被访问
}
else
t[i].left = null; // 空节点
// 处理右子节点
if (cright!= '-')
{
t[i].right = cright - '0'; // 将字符形式的索引转为整数
check[t[i].right] = 1; // 标记此子节点已被访问
}
else
{
t[i].right = null; // 空节点
}
}
// 找到根节点
for (i = 0; i < n; i++)
{
//没有被访问过
if (!check[i])
{
break;
}
}
// 返回根节点索引
root = i;
}
// 返回根节点索引
return root;
}
// 判断两棵树是否同构的递归函数实现
int Isomorphism(int root1, int root2)
{
// 如果两个根节点都为空,返回真
if (root1 == null && root2 == null)
{
return 1;
}
// 如果两个根节点不都为空
else
{
// 如果只有一个根节点为空,返回假
if (root1 == null && root2!= null || root1!= null && root2 == null)
{
return 0;
}
else
{
// 如果两个根节点都不为空且数据不同,返回假
if (T1[root1].data!= T2[root2].data)
{
return 0;
}
// 如果两个根节点数据相同,继续比较子节点
else
{
// 如果两个根节点都没有左子节点,只比较右子节点
if (T1[root1].left == null && T2[root2].left == null)
{
return Isomorphism(T1[root1].right, T2[root2].right);
}
// 如果两个根节点都有左子节点且数据相同,分别比较左右子节点
else
{
if (T1[root1].left!= null && T2[root2].left!= null && T1[T1[root1].left].data == T2[T2[root2].left].data)
{
return Isomorphism(T1[root1].left, T2[root2].left) && Isomorphism(T1[root1].right, T2[root2].right);
}
// 如果两个根节点都有左子节点但数据不同,交换左右子节点进行比较
else
{
return Isomorphism(T1[root1].right, T2[root2].left) && Isomorphism(T1[root1].left, T2[root2].right);
}
}
}
}
}
}