决策智能与强化学习：重放比率（replay ratio）

知乎：DILab决策实验室（已授权）
链接：https://zhuanlan.zhihu.com/p/898641863

0. 概览

近年来，深度强化学习（Deep Reinforcement Learning, DRL）在诸多领域取得了显著的成果。然而，随着网络规模的扩大和训练策略的复杂化，DRL 面临着网络可塑性下降、样本效率低下等挑战。其中，重放比率（Replay Ratio），即梯度更新次数与收集的环境步数之间的比率 [1]，被发现对网络的可塑性和整体性能有着深远的影响。关于神经网络的可塑性的更多分析可参考往期博客：

https://zhuanlan.zhihu.com/p/708244682

本博客旨在探讨重放比率与网络可塑性之间的关系，以及如何利用这一关系来改进 DRL 的性能和扩展能力。为此，我们选取了以下三项代表性的研究工作进行深入分析：

《深度强化学习中的“休眠神经元”现象》[1] 该工作揭示了在高重放比率下，DRL 网络中出现大量休眠神经元，导致网络表达能力受限。作者提出了 ReDo 方法，循环利用这些休眠神经元，以增强网络可塑性。
《更大、更好、更快：具有人类水平效率的 Atari 游戏》[2] 该研究提出了 BBF（Bigger, Better, Faster）Agent，通过扩大网络规模和引入高重放比率与周期性重置机制，在 Atari 100K 基准上实现了超越人类的表现，展示了平衡网络规模与样本效率的可能性。
《深度持续学习中的可塑性丧失》[3] 该论文探讨了在持续学习（continual learning）环境中，深度学习网络如何逐渐失去可塑性的问题。作者提出了持续反向传播等方法，旨在通过引入多样性来维持网络的可塑性。

通过对上述工作的探讨，我们期望深入理解 Replay Ratio 对网络可塑性的影响，并探寻提升 DRL 方法性能的可行路径。

笔者注：为方便读者检索，博客中图片索引保持与原论文中的一致。由于博客篇幅较长，难免有疏忽遗漏之处，敬请读者在评论区讨论指正。电脑端阅读体验更佳。

1. 深度强化学习中的“休眠神经元现象”

1.1 简介

在这项工作中，作者识别出深度强化学习中的“休眠神经元现象”( dormant neuron phenomenon)，即随着训练进行 RL agent 的网络中休眠神经元的比例越来越高（在监督学习中比例一般很低），进而影响了网络的表达能力，而且 replay ratio 越大，越会加剧这种效应。作者在多种算法和环境中展示了这一现象的存在，并强调了它对学习过程的负面影响。为解决这一问题，作者提出了一种简单且有效的方法——ReDo（Recycling Dormant neurons ，循环使用休眠神经元）。实验表明，ReDo 通过减少休眠神经元的数量来维持网络的表达能力，并带来了性能的提升。

官方代码：dopamine/dopamine/labs/redo at master · google/dopamine

1.2 RL 中的神经元休眠现象

定义1: 定义一个神经元的 normalize 后的 (活跃) 分数如下：

当时，称该神经元为 -dormant。注意，同一层的神经元分数之和为1。在本文的分析中，设定。

定义2: 如果一个算法在训练过程中， -dormant 神经元数量逐步上升，则称该算法存在 神经元休眠现象 (Dormant neuron phenomenon)。

1.2.1 DQN 的训练过程中，休眠神经元比例逐渐上升

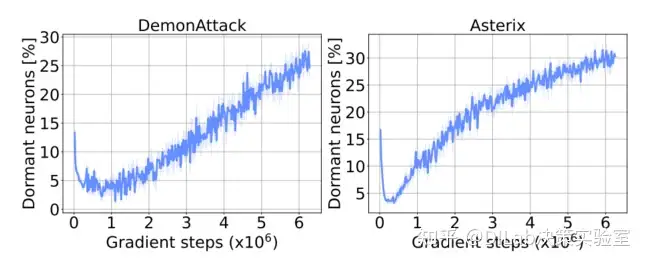论文[1]-图 2: 在 DQN 算法训练过程中，休眠神经元的百分比逐渐增加。

为了显示该现象的普遍性，作者也在下面2个场景下观察到了类似现象：

sample-efficient agent DrQ()的 dormant neuron phenomenon:
连续控制任务中，SAC 的 dormant neuron phenomenon:

1.2.2 非平稳的训练目标加剧了休眠神经元现象

作者比较了两种情况：1）以固定的目标（fixed targets）训练神经网络 2）shuffle 标签，使得训练目标不固定（non-stationary targets）。当训练目标固定时，休眠神经元数量逐渐降低，而训练目标不固定时则显著上升。且每个突然上升的点都对应了 label 被 shuffle 的时间。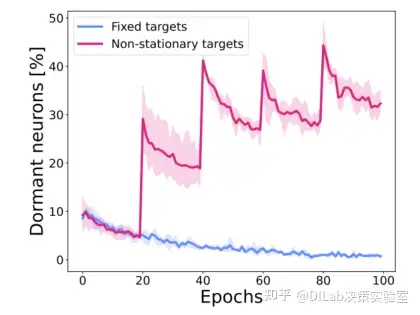论文[1]-图 3:在 CIFAR-10 数据集上，使用固定目标与非平稳目标进行训练时的休眠神经元百分比对比。结果基于 3 个独立实验种子，阴影区域表示 95% 置信区间。使用非平稳目标时，休眠神经元的比例上升。

1.2.3 非平稳的输入并非导致休眠神经元现象的主要因素

为了研究是否是 online 的数据收集会加剧休眠神经元现象，作者也在 offline 设定下的固定数据集上训练 agents，但是休眠神经元的数量还是出现上升，说明input non-stationary 不是休眠神经元现象的主要因素。而当 target 为 fixed targets 时，虽然仍有上升现象，但整体数量较前者少很多。说明非平稳的 target （target non-stationarity）是休眠神经元现象的主要因素之一。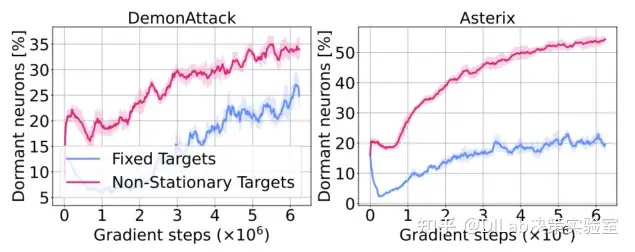论文[1]-图 4:离线强化学习中，使用标准 moving targets （即 non-stationary target）和固定目标训练时的休眠神经元变化。尽管训练数据固定，休眠神经元现象仍然存在。

1.2.4 休眠的神经元将保持休眠

作者比较了不同训练过程中休眠神经元的重叠系数（），重叠系数的上升说明当一个神经元变得休眠后，在接下来的整个训练过程中，它都将保持休眠的状态。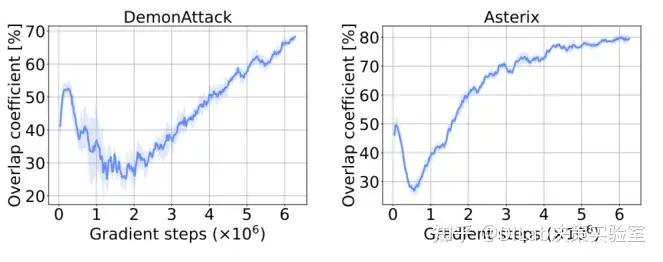论文[1]-图 5:训练过程中休眠神经元的重叠系数变化，显示出保持休眠状态的神经元数量增加。

作者在训练过程中将休眠的神经元进行剪枝，以此确认这些神经元对网络效果的影响。从结果上看，休眠的神经元的移除并不影响网络效果，可以推断出当前休眠的神经元后续也不再活跃。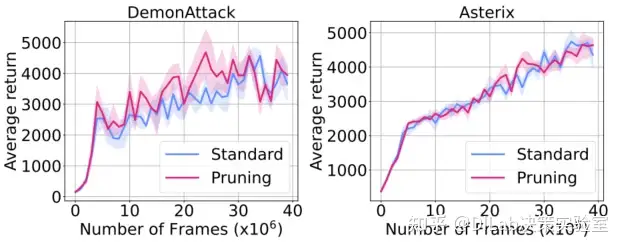论文[1]-图 6:在训练过程中剪枝休眠神经元并未对智能体性能产生显著影响。

1.2.5 replay ratio 越高，休眠神经元越多

在图7中，作者测量了在调整 replay ratio 时神经元休眠的情况，并观察到 replay ratio 与成为休眠状态的神经元比例之间有很强的相关性。尽管难以下结论，但这一发现或许可以解释在高重放比例下训练强化学习 agent 时的困难（将在下文验证，回收休眠神经元并激活它们可以缓解这种不稳定性，从而带来更好的效果。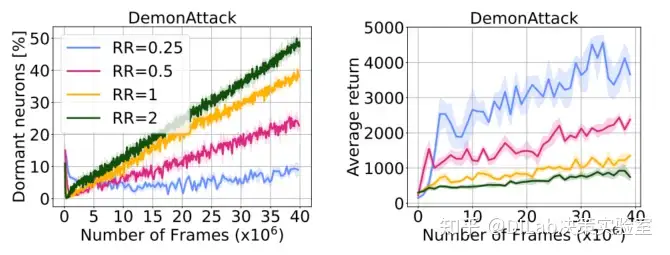）论文[1]-图 7:不同重放比率（RR）条件下休眠神经元增加的速率（左）。随着回放比率的提升，休眠神经元的比例也随之增加。右图显示，较高的休眠神经元百分比与性能下降相关。

1.2.6 休眠神经元导致学习新任务更困难

作者首先以 replay ratio=1 训练了一个 DQN agent，然后微调该网络，使其输出朝着一个更好的 DQN agent 网络的输出逼近。另一方面，以相同的 target 和训练 loss，训练一个随机初始化的网络。由于预训练的 agent 中休眠神经元更多，因此 loss 无法下降，说明其学习新任务更加困难。且在训练过程中，该网络的休眠神经元还在逐步上升。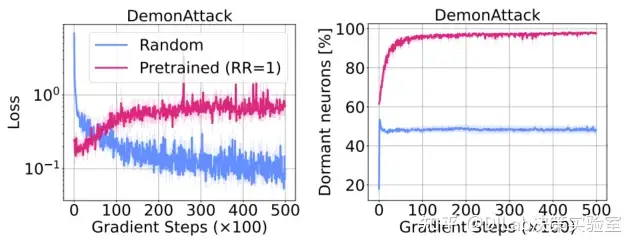论文[1]-图 8:预训练网络中出现的休眠神经元在拟合固定目标时表现不如随机初始化网络。结果为 5 个实验种子的平均值。

1.3 Recycling Dormant Neurons （ReDo）方法

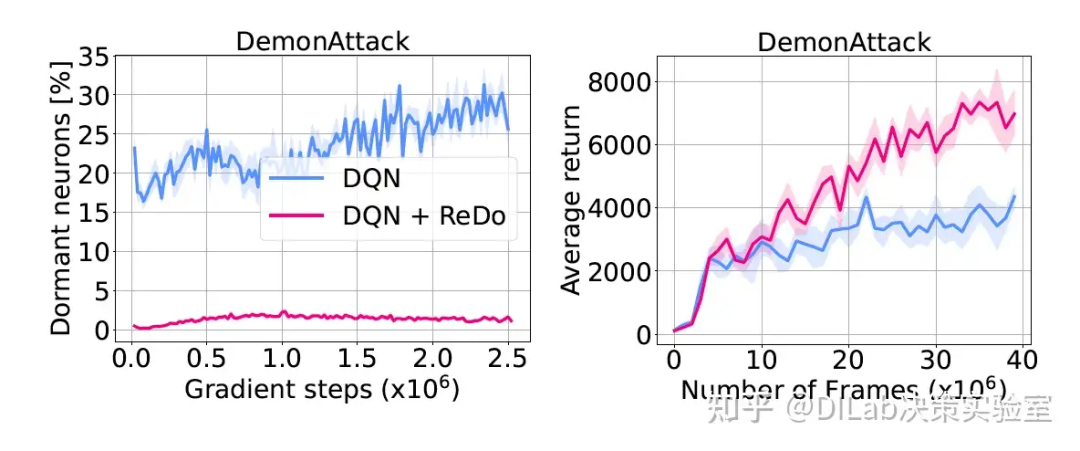在训练过程中，以频率 F 检查所有层，将所有 -dormant 的神经元的输入权重重置为原先的初始化分布，而输出权重设置为0。在加入 ReDo 后，DQN 的休眠神经元大幅减少，同时效果也随之提升。论文[1]-算法1 ReDo。论文[1]-图 9: ReDo 效果评估（τ = 0.025），左图展示其减少休眠神经元的表现，右图则展示其提升 DQN（RR = 0.25）性能的效果。

1.3.1 不同回收策略

在输入权重上，作者尝试了重置为活跃神经元权重范数的平均值，效果与重置为初始化权重相似。而输出权重上，作者尝试了将输出权重置为随机值，其效果近似于重置为0或更差。

1.3.2 ReLU 是否是导致神经元休眠的原因

RL 的网络中一般使用 ReLU，其在零值上的梯度为零。为了探究这一激活函数是否会产生影响，作者比较了使用 ReLU与 Leaky-ReLU 的性能。实验结果表明，虽然 Leaky-ReLU 相对于 ReLU 会减少一些休眠神经元数量，但并未有效解决这一问题。

1.4 实验

1.4.1 基线结果

作者比较了不同设定下，ReDo 对 RL 算法的效果影响。可以观察到，ReDo 对效果的影响对于较高的 replay ratio更为显著。同时，在不同的 n-step，网络结构和算法下，ReDo 都能够有效地提升效果。论文[1]-图 10:不同回放比率下，使用和不使用 ReDo 的效果对比。从左至右分别为：默认 DQN、3 步 TD 目标 DQN、ResNet 架构 DQN 及 DrQ(ϵ)。结果基于 5 个实验种子，DrQ(ϵ) 使用了 10 个种子，误差条表示 95% 置信区间。

1.4.2 分析

作者猜测默认的 learning rate 可能是导致在高 replay ratio 下效果不好的原因。一般来说，一次数据收集后进行的训练步数越多，学习率应该越低。因此在 replay ratio=1 下，作者将学习率降低四倍，但是仍然观察到较高的休眠神经元数量。而在加入 ReDo 后，休眠神经元数量明显降低。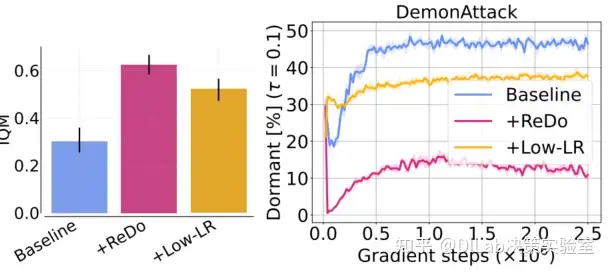论文[1]-图 11:在高回放比率下，降低学习率的效果评估。调整学习率有助于改善性能，但未能根本解决休眠神经元问题。左图为 17 个游戏的汇总结果，右图为 DemonAttack 游戏中休眠神经元的百分比变化。

在先前的研究中发现，over-parameterized network 能够拟合新的目标，因此可以猜测 over-parameterization也能够解决休眠神经元的问题。因此作者增加了 DQN 网络的宽度。然而从下图中可以看到，over-parameterization 对效果的提升远低于 ReDo 带来的影响。而从休眠神经元的数量来看，可以发现 ReDo 实际上对参数更多的网络有更明显的帮助。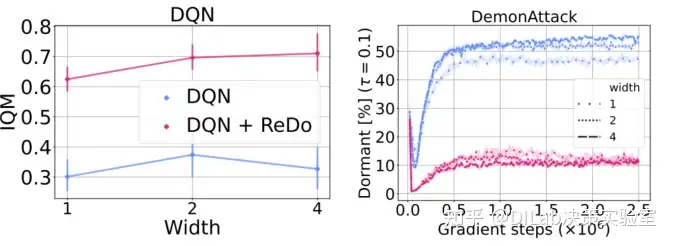论文[1]-图 12:不同网络宽度下 DQN（RR = 1）的性能表现。增加网络宽度略微提升性能，但效果不及 ReDo 的增益。ReDo 在不同网络规模下均能提升性能。

作者还比较了 ReDo 与其他先前工作中对于 replay ratio 提升的解决方案，如周期性 reset 网络和添加 weight decay。ReDo 相较于这两种方法都效果更好。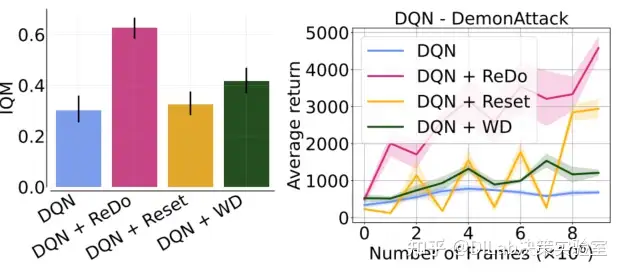论文[1]-图 13:ReDo 与两种正则化方法（Reset 和权重衰减（WD））在训练 DQN 智能体时的性能对比。左图为 17 个游戏的汇总结果，右图为 DemonAttack 游戏的学习曲线。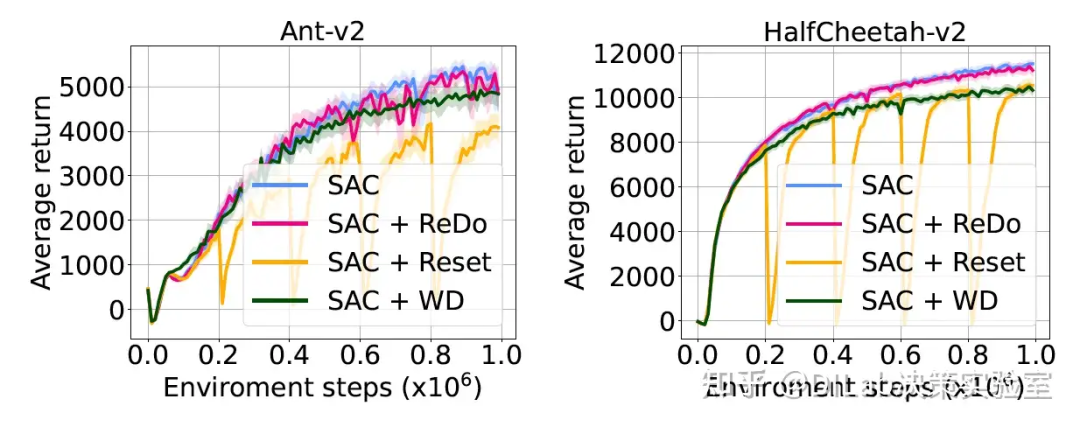论文[1]-图 14:ReDo 在 SAC 智能体中的效果，与 Reset 和权重衰减（WD）方法进行对比。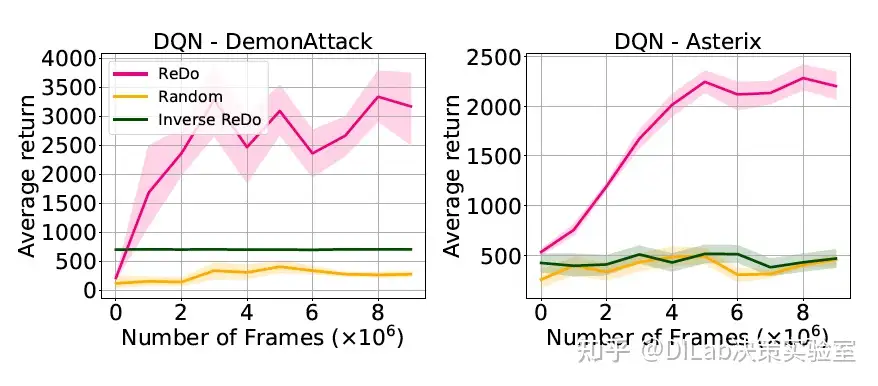论文[1]-图 15:不同神经元回收策略的比较。回收得分最高的神经元（逆 ReDo）或随机选择神经元均会导致性能下降。

2. BBF Agent

2.1 简介

论文[2]的作者提出了一种基于价值的强化学习agent，称为BBF（Bigger, Better, Faster）。该agent在Atari 100K基准测试中取得了超越人类的表现。BBF依赖于扩大用于价值估计的神经网络规模，以及一系列设计选择，其中主要设计在于高的replay ratio和周期性重置机制，这些重置可能在避免灾难性遗忘和保持网络可塑性之间达到了一个理想的平衡。作者对这些设计做出了详尽的分析，并为未来的研究提供了有价值的见解。最后，作者讨论了有关更新ALE上样本高效RL研究目标标准的建议。

官方代码：https://github.com/google-research/google-research/tree/master/bigger_better_faster

2.2 方法

本研究的核心问题是如何在样本稀少的条件下扩展深度强化学习中的网络规模。为此，研究聚焦于Atari 100K基准，其中agent仅能与环境进行10万步的交互。该基准为多个Atari 2600游戏提供了多样性和挑战性，但在这种有限的交互条件下，扩大网络规模往往难以维持性能，甚至可能导致性能下降。

BBF Base Agent

作者提出了“Bigger, Better, Faster”（BBF）agent，它在Atari 100K基准上实现了超越人类的表现，并在单块GPU上仅耗时约6小时。BBF的核心在于多个改进技术的集成，显著提升了现有强化学习方法在样本稀少场景下的表现。图2展示了BBF相较于几种表现优秀的Atari 100K agent的强大性能表现，包括EfficientZero、SR-SPR和IRIS。

BBF基于Dopamine框架实现，评估过程中使用了reliable工具中的四分位平均（IQM）指标来衡量性能。BBF的基础agent是修改后的SR-SPR agent，通过周期性网络重置和高重放比率（原SR-SPR的RR是16，BBF的RR=8）来提高采样效率。为了减少计算成本，作者在实验中还展示了RR=2的BBF及其消融实验结果。

BBF的改进技术

扩展网络规模是本研究的重要动机。BBF采用了15层的ResNet架构Impala-CNN，并将每层的宽度扩展了4倍。实验表明，BBF的性能随着网络宽度的增加而持续提升，而其他baseline方法在较小的网络扩展下已达到性能瓶颈。最终，作者选择了4倍宽度以平衡计算成本与性能提升。
更严格的参数重置：原始的SR-SPR agent在卷积层使用了一种收缩-扰动（shrink-and-perturb）方法，其中参数仅向随机目标扰动20%，而后续层则完全重置为随机初始化。作者发现将卷积层参数的扰动幅度从20%提升至50%，增强了网络的正则化效果，提升了大型网络的性能。
递减的更新步长：BBF引入了递减的更新步长策略。更新步长在每次网络重置后的前1万次梯度更新中从10指数递减至3。这一策略受到Kearns & Singh（2000）理论的启发，能够在加快收敛速度的同时减少最优值函数的渐近误差（n越大收敛速度越快，但是渐近误差越大）。
动态折扣因子：BBF采用了动态折扣因子，从初始值0.97逐渐递增至0.997。逐步增大的提高了对延迟奖励的权重，实验表明这一动态调整策略优于固定折扣值。
权重衰减：为抑制过拟合，作者为BBF引入了权重衰减（使用了AdamW优化器），并设置了权重衰减系数为0.1。实验显示，在较高重放比率下，权重衰减极大地提升了性能。
移除NoisyNets：由于NoisyNets引入的噪声未能带来预期的性能提升（可能由于策略频繁变化引发过度探索，或者向优化过程中引入了更多的方差），反而增加了计算开销，作者选择移除该组件。实验表明，移除NoisyNets对性能没有显著影响，但显著减少了计算资源的消耗。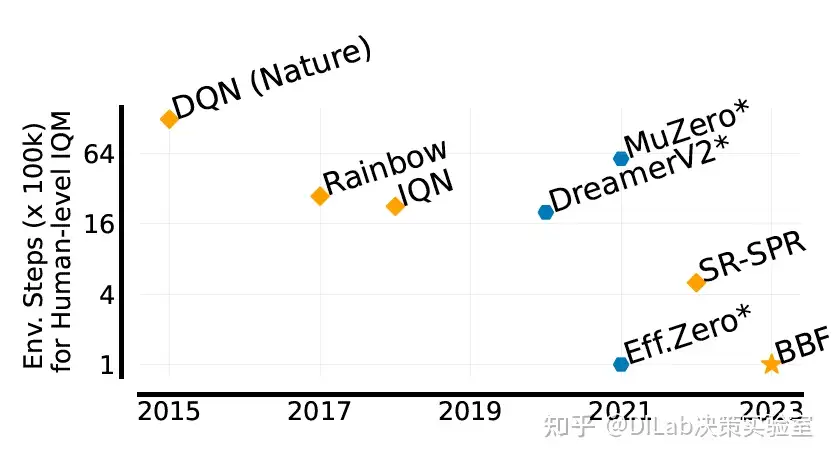论文[2]-图1 基于26个游戏的IQM，展示了不同智能体在达到人类水平表现时需要的环境步数（越低越好）。无模型智能体BBF在样本效率上相较于SR-SPR提升了5倍，相较于传统的无模型强化学习方法（如DQN、Rainbow和IQN）提升了至少16倍。还将DreamerV2、MuZero Reanalyse和EfficientZero纳入参考。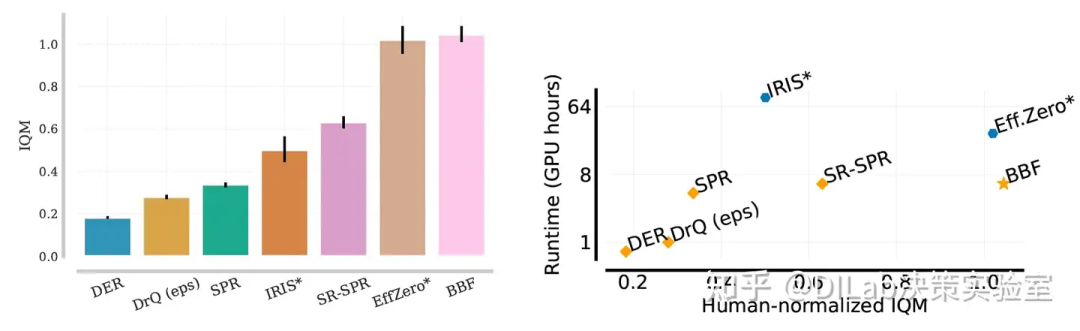论文[2]-图2 在Atari 100K任务上，本文提出的无模型BBF智能体与多种无模型智能体（包括SR-SPR、SPR、DrQ（eps）、DER）以及基于模型的智能体（包括EfficientZero和IRIS）的性能和计算成本的比较。（左）在人类标准化IQM上，BBF的表现优于所有对比的智能体，误差条表示95%的自助法置信区间。（右）计算成本与性能的对比，基于26个游戏的人类标准化IQM。BBF的性能比SR-SPR提升了2倍，且计算成本几乎相同；与基于模型的EfficientZero相比，BBF的性能相当，但运行时间减少了至少4倍。运行时间通过各个环境中所使用的A100 GPU的总运行小时数衡量。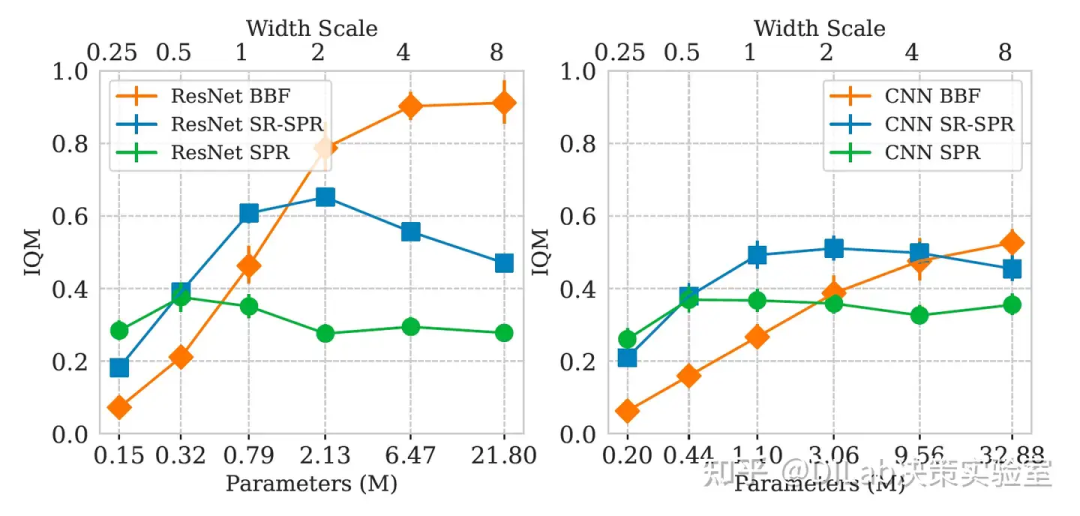论文[2]-图3 通过扩展ResNet和CNN架构的网络宽度，比较了BBF、SR-SPR和SPR在重放率为2时的性能，分别基于Impala的ResNet架构（左）和标准的3层CNN架构（右）。本文报告了IQM表现，并附带95%置信区间的误差条。x轴显示了不同配置的大致参数数量及其相对于默认值的宽度比例（宽度比例=1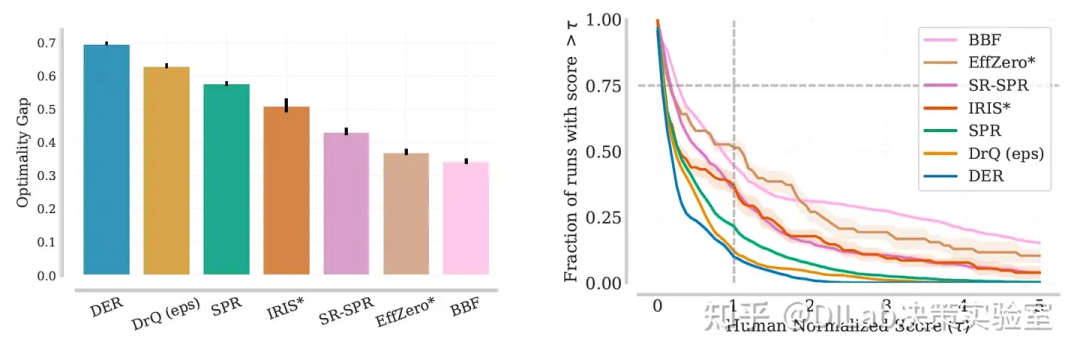）。论文[2]-图4 BBF在Atari 100K任务上，以重放率为8时的最优性差距（数值越低越好）与其他算法进行了比较。误差条表示95%的置信区间，BBF的最优性差距低于所有对比算法，表明其在所有任务上更接近人类水平。（右）表现曲线展示了所有运行结果及26个游戏在训练结束时的得分分布（得分越高越好）。曲线下的面积表示算法的平均表现，曲线与y=0.75相交处的τ值代表其25分位表现。BBF在某些对IQM或中位数表现影响较小的难题任务上表现尤为出色。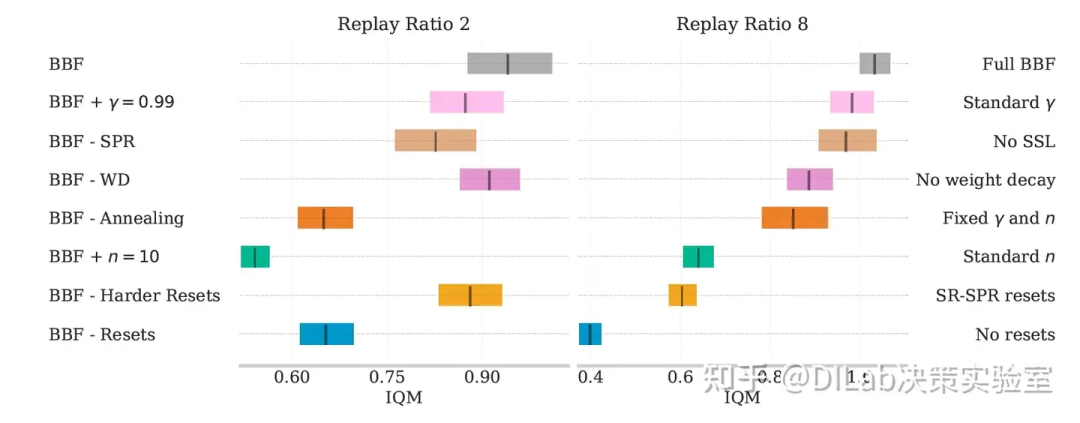论文[2]-图5 评估移除BBF各组成部分对性能的影响，重放率设定为2和8。报告结果为26个Atari 100K游戏的四分位间均值（IQM），误差条表示15次独立运行的95%置信区间。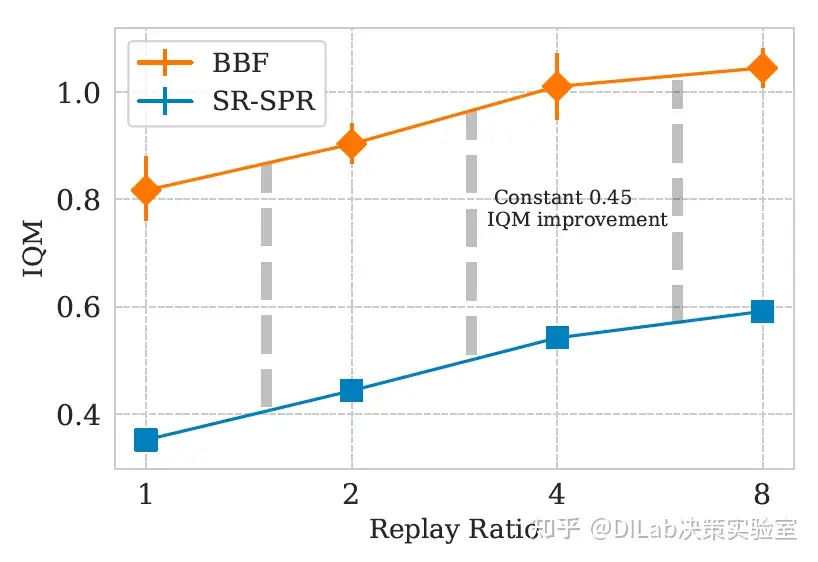论文[2]-图6 BBF与SR-SPR在不同重放率下的性能对比。每个数据点显示了四分位间均值（IQM）及其95%置信区间。在所有重放率下，BBF相较于SR-SPR的表现提升保持稳定，约为0.45 IQM。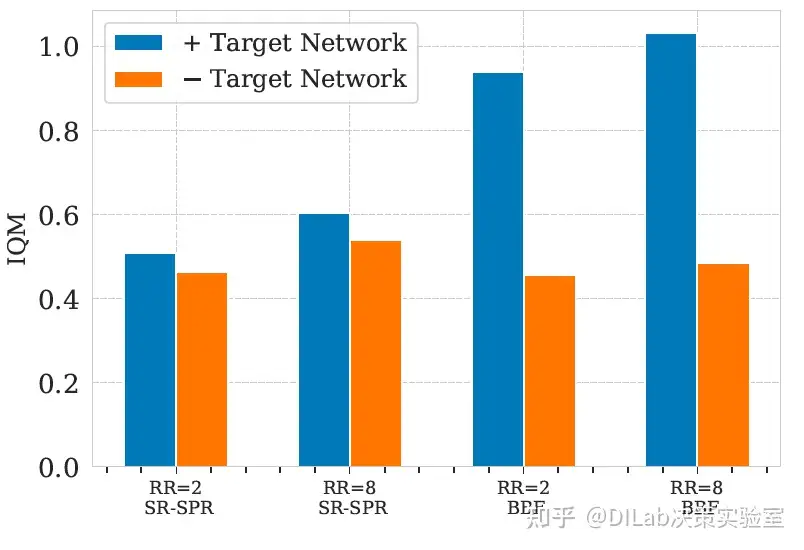论文[2]-图7 比较BBF与SR-SPR在重放率为2和8时，使用或不使用EMA目标网络情况下的表现。评估基于26个Atari 100K游戏的人类标准化四分位间均值（IQM）。

2.3 分析

鉴于BBF组件的重要性，作者探讨了这些发现可能对其他算法产生的影响。

自监督学习的重要性：研究表明，在样本有限的场景中，结合任务一致的自监督目标可以加速学习。实验证明，移除BBF中的SPR目标会显著降低性能（图5），且EfficientZero与BBF的自监督目标高度相似，这是两者的关键共同点。
增加梯度更新次数可以提高样本效率：在数据较少的情况下，增加梯度步骤通常更为有利，但注意的是许多算法在缺乏额外正则化的情况下难以从中获益。原始DQN的replay ratio为0.25，而BBF在较高replay ratio下表现更优，与SR-SPR的线性关系一致，且BBF整体表现略好（BBF的表现大约比SR-SPR高出0.45 IQM）（图6）。这一现象提示replay ratio与网络扩展之间的关系值得进一步探讨。EfficientZero的replay ratio虽然只有1.2，但考虑其较大的批量大小，其effective replay ratio与BBF相当。
目标网络的重要性：过去的研究认为其对样本效率无益，但最新研究表明，特别是在高replay ratio下，目标网络能够略微提升性能（图7）。随着网络扩展，目标网络的使用在所有replay ratio下变得更加重要。
重置机制在高replay ratio下的重要性：周期性重置可能通过减少过拟合来增强算法的稳定性（图5和图8）。相比之下，使用比SR-SPR更大的侵略性扰动带来了更多的性能提升。
单靠扩大网络规模并不足以提高性能：单纯扩大SR-SPR所使用的CNN容量无法提升性能。相反，正如图3所示，SR-SPR的性能随着网络规模的增加而下降。较小的Impala-CNN ResNet（以参数和FLOPs衡量）在所有宽度扩展下表现更好。
计算效率：随着机器学习方法的复杂性不断增加，计算效率这一指标常常被忽视。虽然EfficientZero的训练时间约为8.5小时，但它需要大约512个CPU核心和4个分布式GPU。而IRIS每次运行则需要半个A100 GPU，耗时一周。SR-SPR在其最高replay ratio 16时，使用25%的A100 GPU和一个单独的CPU，耗时约24小时。相比之下，作者的BBF agent在replay ratio为8时，仅用一个CPU和半个A100 GPU运行10小时。因此，从GPU小时数来看，BBF在性能与计算资源之间提供了最佳的权衡（见图2）。
重新审视Atari 100k基准的价值与挑战：虽然EfficientZero和BBF已在Atari 100k基准上实现了人类水平的表现（IQM≥1.0），但该基准仍有研究价值。IQM作为聚合度量，掩盖了个别游戏的表现差异。正如图4所示，各算法在某些游戏上仍未完全达到人类水平，最优差距（optimality gap）未归零，也即尚无算法能在所有26个游戏中均达到人类表现。此外，Atari 100k基准仅包含ALE套件中的26个游戏，并未包含粘性动作（sticky actions，环境以25%的概率执行上一步动作，而不是agent给出的动作，这会导致任务难度增加）。尽管如此，BBF在全套55个游戏中的表现依然出色，粘性动作对其影响较小（如图9所示）。未包含在Atari 100k中的游戏通常更具挑战性，但BBF在这些游戏中的表现优于部分基线算法（如DQN），特别是在困难游戏上（见图8和图11）。
BBF的性能与研究前沿：BBF在标准Atari环境中表现卓越，在两小时内达到了DQN 256小时的表现（图10）。这一结果为社区设定了新的研究目标，即在两小时内达到Rainbow的表现。为鼓励进一步研究，作者公布了55个带粘性动作的游戏得分，推动了更广泛的性能测试。
数据扩展与BBF的优势：作者通过延长训练至100万步，探讨了样本效率高的算法在更长训练时间下的表现。尽管SPR和SR-SPR的性能趋于平稳，且两者差异在100万步时消失，BBF仍持续领先，并在不到20万步时超越了DQN，最终匹配了Rainbow的表现（图12）。值得注意的是，这一训练成本仅为replay ratio为8时的2.5倍。因此，作者建议研究人员在资源有限的情况下采用这种设置，特别是BBF在极少数据下（如2万或5万步）仍优于近期提出的算法（图13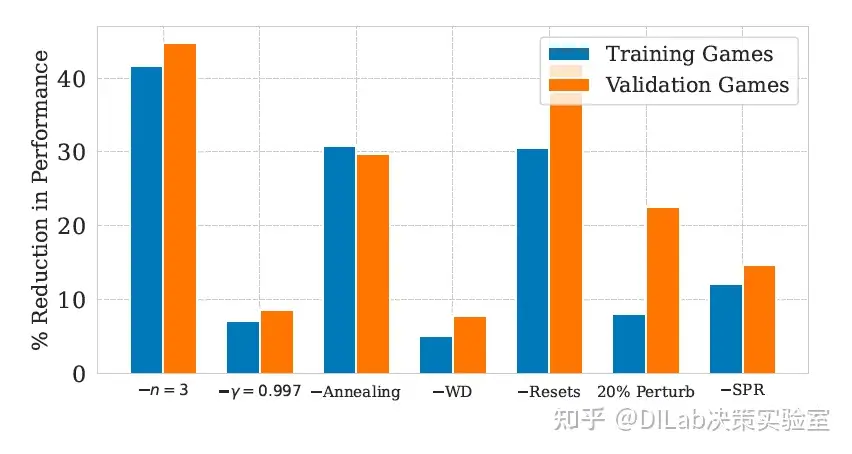）。论文[2]-图8 在29个未见过的游戏中验证BBF的设计选择，重放率为2。尽管训练集仅包含26个Atari 100K游戏，作者依然在ALE环境中29个未见游戏上评估了BBF各组件的表现。这些游戏不属于Atari 100K集合。值得注意的是，所有BBF组件在未见过游戏中的性能均显著提升。具体而言，报告了相对于完整BBF智能体在重放率为2时的人类标准化IQM的百分比下降。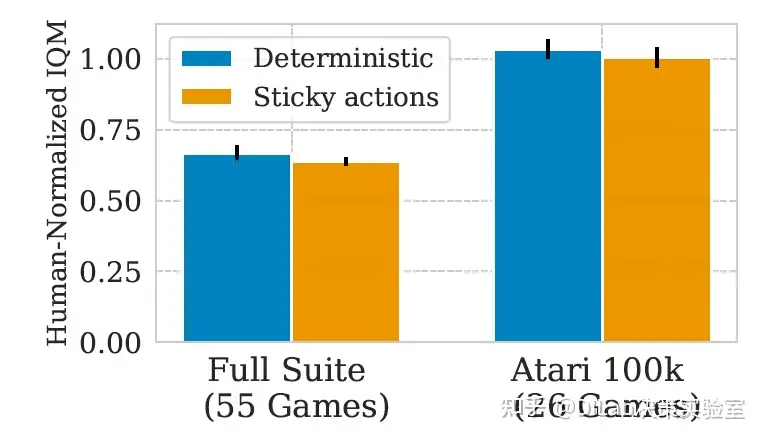论文[2]-图9 评估BBF在有或无粘滞动作影响下的ALE表现。报告了在重放率为8时，26个Atari 100K游戏及ALE中全部55个游戏的人类标准化IQM表现。尽管在全部55个游戏上的表现略有下降，但粘滞动作对两种设置下的表现影响不显著。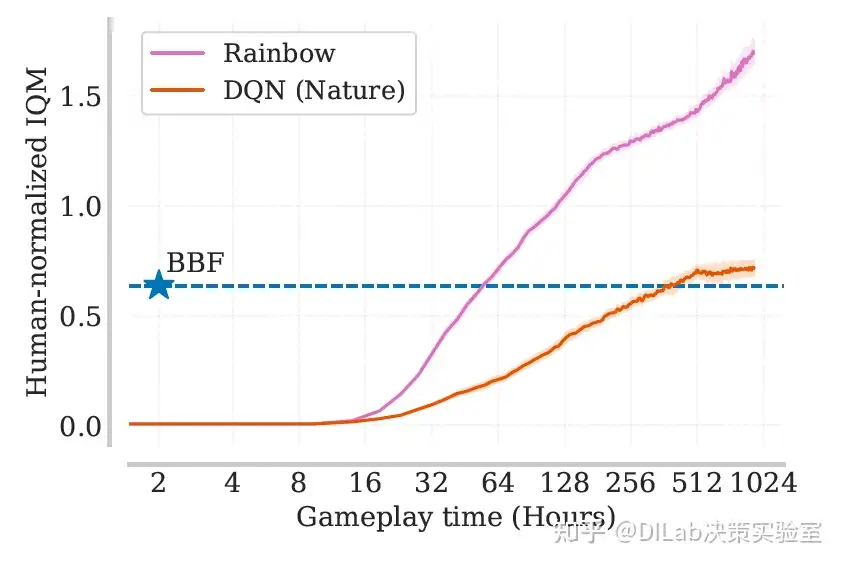论文[2]-图10 展示ALE环境中样本效率的进展，基于55个带粘滞动作的Atari游戏的人类标准化IQM表现，作为人类游戏时间的函数。在重放率为8时，BBF的表现随样本量增加而提升，阴影区域表示95%置信区间。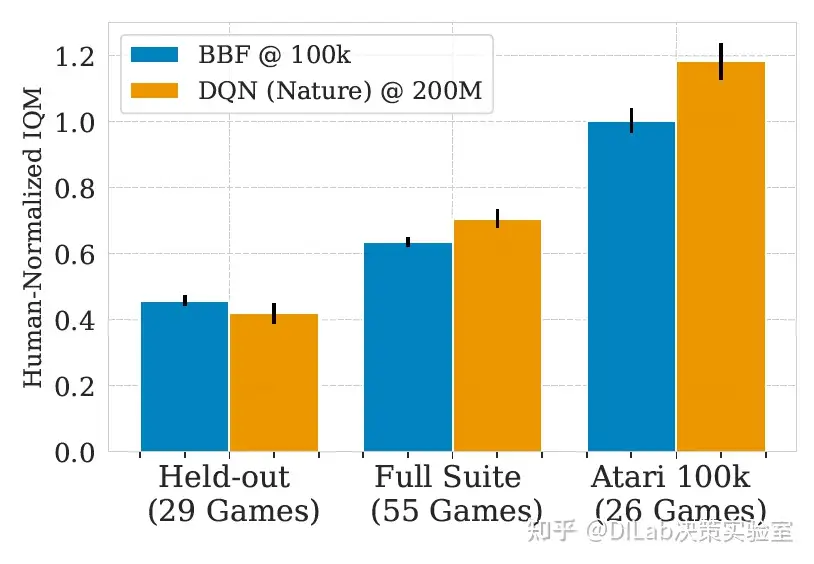论文[2]-图11 比较BBF在29个未见游戏与26个Atari 100K游戏中的表现。在重放率为8并带有粘滞动作的情况下，BBF在100K步的训练表现大致与DQN（Nature）在每个游戏上使用500倍训练数据的表现相当。尽管作者发现不在Atari 100K训练集中的29个游戏比26个Atari 100K游戏更难，但没有证据表明BBF相较于DQN对Atari 100K过拟合。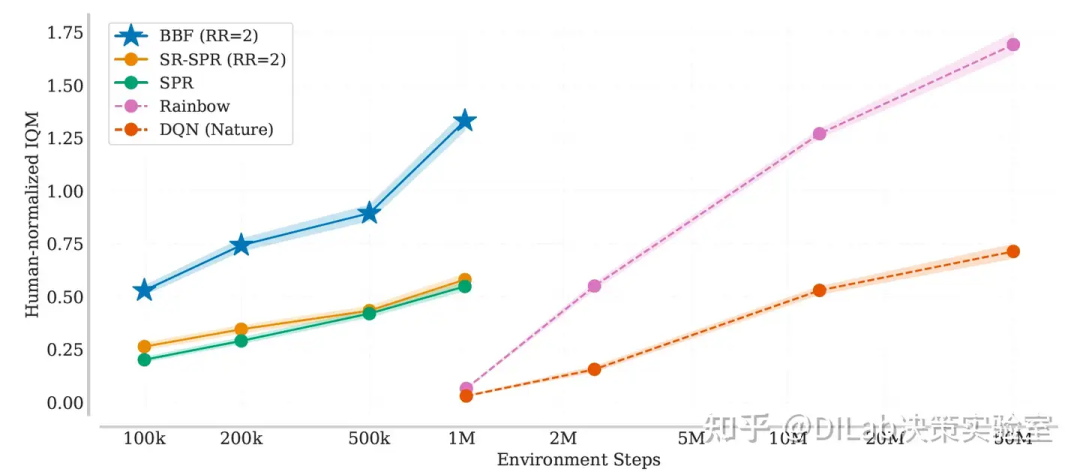论文[2]-图12 展示BBF、SR-SPR和SPR在重放率为2时的学习曲线，基于55个带粘滞动作的Atari游戏的人类标准化IQM表现，作为环境交互次数的函数。阴影区域表示95%置信区间。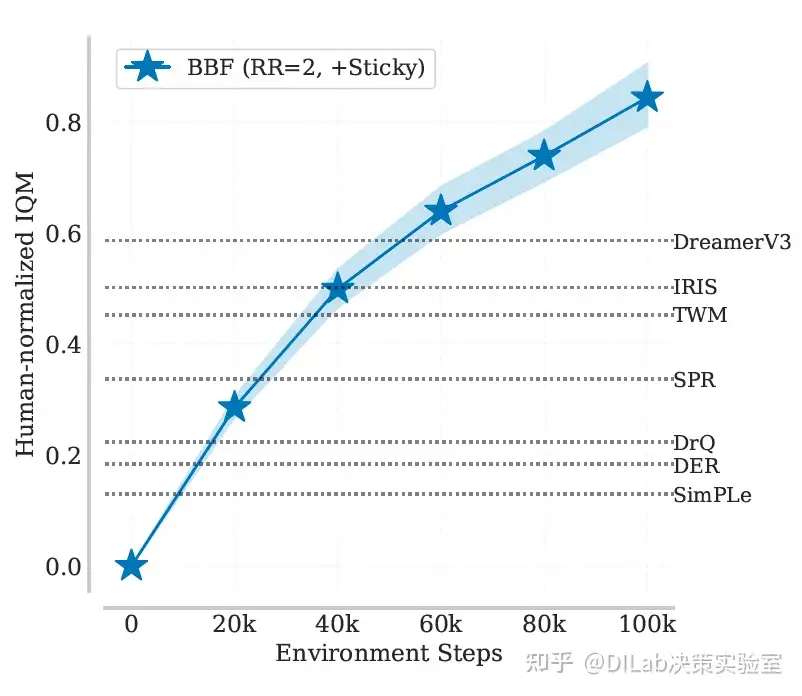论文[2]-图13 展示BBF在重放率为2并带有粘滞动作时，26个Atari 100K游戏的人类标准化IQM学习曲线，并对比多个近期算法在100K步训练后的最终表现。即使在50K步时，BBF的表现已超越所有其他算法，尽管在后期性能有所下降。

3. Loss of Plasticity in Deep Continual Learning

3.1 简介

人工神经网络、深度学习方法和反向传播算法构成了现代机器学习和人工智能的基础。这些方法几乎总是分成两个阶段使用：一个阶段更新网络的权重，另一个阶段则在权重保持不变的情况下使用或评估网络。这与要求持续学习的自然学习和许多应用场景刚好相反。在持续学习环境中，深度学习方法是否有效一直不明确。在此，作者表明它们并不有效——标准的深度学习方法在持续学习环境中逐渐失去可塑性，直到它们的学习效果与浅层网络无异。作者通过经典的ImageNet数据集和强化学习问题，展示了在网络结构和学习算法的广泛变化范围内，这种可塑性的丧失。只有那些不断向网络注入多样性的算法才能无限期地维持可塑性，例如作者的持续反向传播算法，这是一种反向传播的变体，其中一小部分较少使用的单元会持续并随机地重新初始化。作者的结果表明，基于梯度下降的方法并不足够——要实现持续的深度学习，需要一个随机的、非梯度的成分来维持多样性和可塑性。

官方代码：https://github.com/shibhansh/loss-of-plasticity

3.2 超监督学习中的可塑性丧失

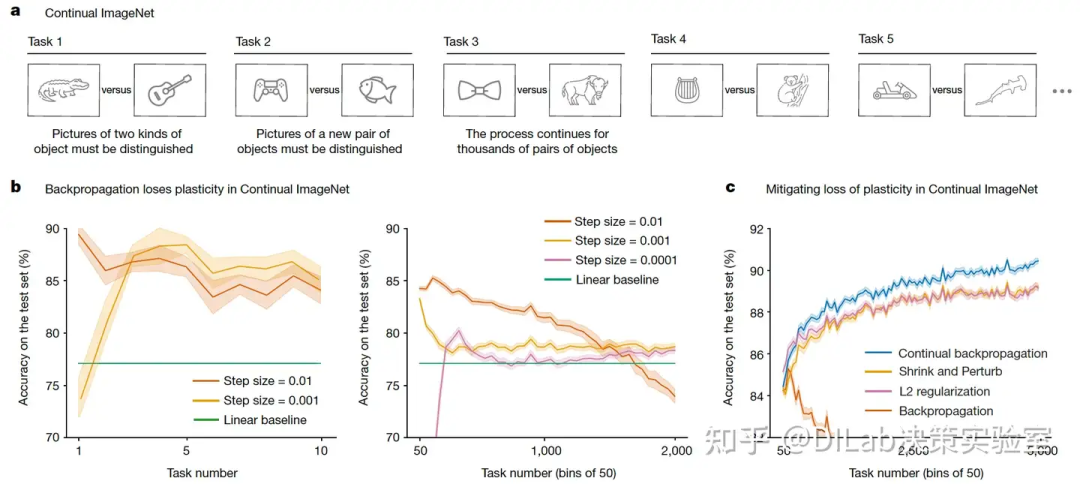图1：Continual ImageNet中的可塑性丧失。在基于ImageNet图像的二元分类任务序列中(a)，传统的反向传播算法在所有步长下都表现出可塑性丧失(b)，而持续反向传播、L2 正则化以及 Shrink and Perturb 算法则能够长期保持可塑性(c)。所有结果均为30次实验的平均值；其中，实线表示均值，阴影区域表示±1个标准误差。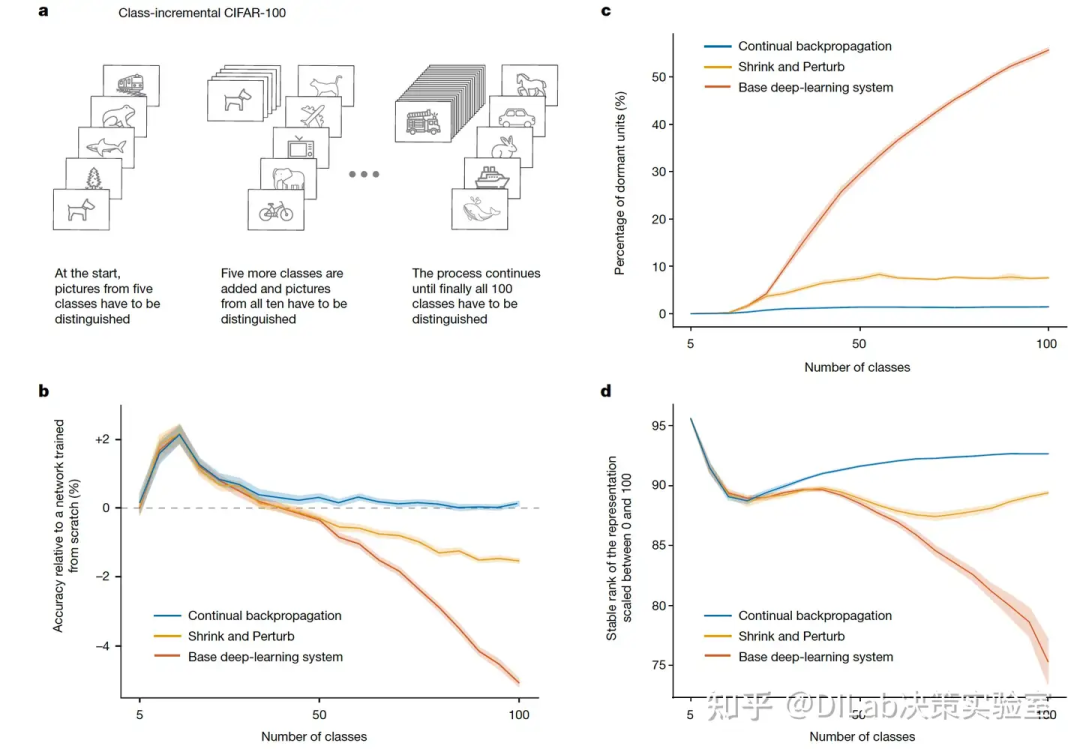图2：class-incremental CIFAR-100中的可塑性丧失 a，class-incremental图像分类任务，学习系统会随着时间的推移逐渐接触到更多的类别，并在更多的类别上进行学习和测试，细节参考原论文。b，最初，增量训练相较于从头开始训练的模型可提高准确率，但在训练到40类之后，基础深度学习系统的准确率显著下降，而Shrink and Perturb学习系统的准确率下降较少，基于持续反向传播的系统则完全无下降。c，在基础深度学习系统中，活动时间少于1%的网络单元数量迅速增加，而Shrink and Perturb以及持续反向传播系统中的增长则较少。d，低stable rank（其定义详见下文）表明网络单元无法提供足够的多样性；基础深度学习系统的多样性丧失远高于Shrink and Perturb和持续反向传播系统。

本文旨在展示标准深度学习系统中的可塑性丧失现象。为确保结果的严谨性，作者系统性地考察了多种深度学习网络、学习算法和参数设置，并通过长时间实验和多次重复验证，获得了统计显著的结果。由于计算资源的限制，使用如大型语言模型进行全面研究的成本过高，难以实现。然而，随着硬件的发展，早期的深度学习网络和经典测试问题仍可用于系统研究。为此，作者选择了ImageNet这一经典的物体识别平台，并将其转化为一个持续学习问题，即“Continual ImageNet”。

ImageNet数据集包含数百万张按类别标注的图像，标准任务是根据图像推测其类别。为了构建持续学习任务，作者将1,000个类别两两配对，生成50万个二分类任务。每个任务中，网络先在两个类别的图像上训练，再在独立的测试集上评估表现。任务逐个进行，网络在完成一个任务后进入下一个类别对的训练和测试。任务的难度保持不变，网络性能的下降则表明其学习能力的减弱，即可塑性丧失。

实验结果显示，尽管深度学习网络在早期任务中表现优异，测试准确率可达88%，但在经历了2,000个任务后，无论采用何种超参数配置，网络的可塑性均已显著下降，验证了可塑性丧失现象的存在。

对于一个矩阵，其奇异值按降序排列，且，稳定秩 (stable rank) 定义为满足以下条件的最小：

3.3 强化学习中的可塑性丧失

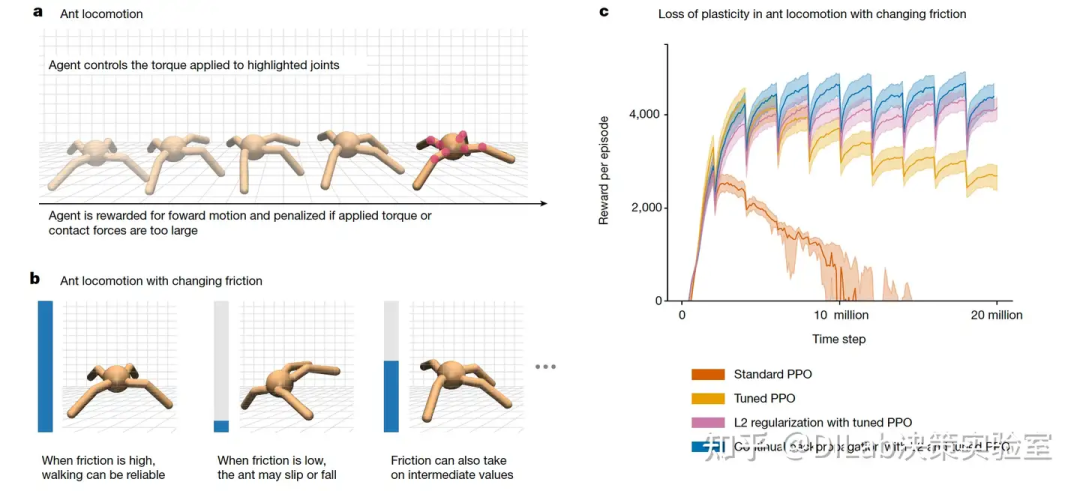图3：非平稳强化学习任务中的可塑性保持 a，强化学习agent控制模拟Ant的八个关节（红色圆圈）以最大化前进速度并最小化惩罚。b，在作者使用的Ant任务版本中，每隔200万时间步会改变地面的摩擦力。c，标准的PPO学习算法在非平稳Ant任务中出现灾难性失败。虽然对PPO的优化器（Adam）进行定制调优可以缓解这一问题，但要实现长期良好的表现，仍需引入持续反向传播或L2正则化。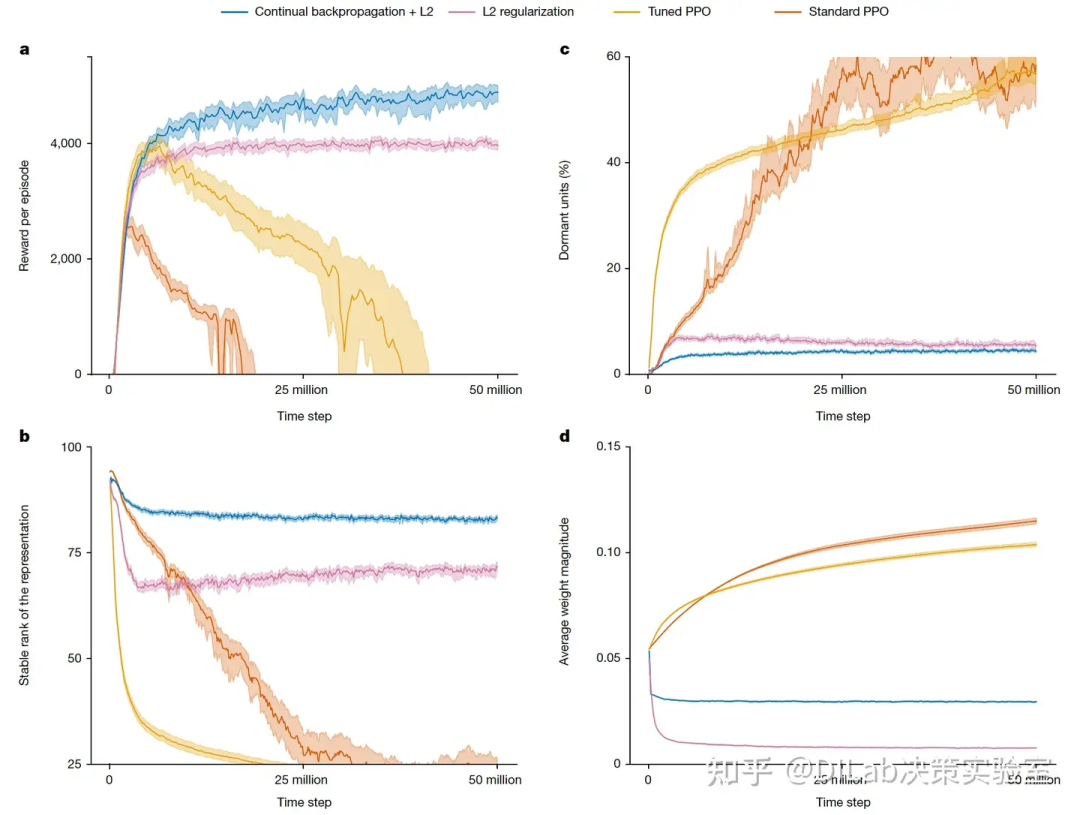图4：平稳Ant运动任务中的结果 a，四种强化学习算法在该问题中的表现与在非平稳问题中的表现类似（参见图3c）。b,c，对网络内部的进一步分析显示出与监督学习类似的模式（参见图2c,d）。d，在标准和调优的PPO下，网络权重的绝对值稳步增加，而在加入或不加入持续反向传播的L2正则化情况下，权重则逐渐减少并保持较小值。

在强化学习中，持续学习的重要性远超于监督学习。这不仅是因为环境可能会动态变化，还因为agent的行为改变会影响其接收到的数据，即便环境本身是静态的。因此，强化学习中对持续学习的需求尤为突出，也是深度学习中可塑性丧失的典型场景。然而，系统性地展示强化学习中的可塑性丧失具有挑战性，部分原因在于强化学习算法和实验设置的多样性。算法可能学习价值函数、行为策略，或两者的结合，且可能涉及回放缓冲区、世界模型或潜在状态的学习。此外，实验设置可能是分阶段的、持续的或离线的，这些因素都增加了实验复杂性。更深层次的问题在于，强化学习算法会影响代理所能接触到的数据，因此算法的学习能力与其生成有用数据的能力密切相关。这使得强化学习的结果比监督学习更加随机和波动，展示其能力尤其是负面结果，往往需要更多的实验运行和工作，难以得出明确结论。

作者的第一个示例涉及一种应用于模拟Ant型机器人的强化学习算法，该机器人的任务是尽可能快速且高效地向前移动。agent与环境的交互由一系列回合组成，每个回合从一个标准状态开始，持续最多1000个时间步。在每个时间步，agent会根据前进的距离和动作的幅度获得奖励（具体细节见方法部分）。如果Ant跳得太高而未能前进，回合会提前结束，这种情况通常发生在学习初期。在接下来的结果中，作者使用回合期间的累计奖励作为主要性能衡量指标。为了使任务变得非平稳（从而强调可塑性），作者每经过200万时间步就改变一次Ant脚与地面之间的摩擦系数（但仅在回合边界处改变；详见方法部分）。为实现最快的行走速度，agent每次摩擦系数改变时都必须重新学习其行走方式。

在这一实验中，作者使用了近端策略优化（PPO）算法。PPO是一种基于反向传播的标准深度强化学习算法，广泛应用于机器人学、实时策略游戏以及通过人类反馈微调大语言模型。在最初的200万时间步内，PPO表现良好（见图3c中的红线），直到第一次摩擦系数改变，此后表现逐渐恶化。值得注意的是，图3c中的其他算法在每次摩擦变化时表现也有所下降，但随后agent能够适应新的摩擦，性能逐步恢复，形成锯齿状模式。而使用经过特殊调整的Adam优化器增强的PPO表现更优（具体细节参见后文方法一节，见图3c中的橙线），但在摩擦系数多次变化后，其表现仍然显著下降，表明可塑性大幅丧失。相比之下，使用L2正则化和持续反向传播增强的PPO在面对任务变化时更好地保持了可塑性。

接下来，作者探讨相同的Ant运动任务，但摩擦系数保持在一个中间值，持续5000万时间步。图4a中的红线显示，PPO的平均性能在约300万步后有所提升，但随后急剧下滑。在2000万步后，Ant每个回合都失败，再也无法有效前进。图4的其他面板进一步揭示了PPO的可塑性丧失。结果表明，网络可能以类似于监督学习中的方式丧失了可塑性（参见图2和扩展数据图3c）。无论是强化学习还是监督学习，网络的大多数单元在训练期间变得休眠，导致网络丧失了stable rank。通过L2正则化防止权重的持续增长，减缓了性能的退化，但也导致权重非常小（见图4d），阻碍了agent形成有效的行为。而加入持续反向传播的表现则更为优异。作者仅展示了带有轻微L2正则化的持续反向传播的结果，因为在没有正则化的情况下，性能对参数设置极为敏感。结果表明，可塑性丧失在深度强化学习和深度监督学习中都可能产生灾难性的影响。

3.4 保持可塑性

令人意外的是，像Adam、Dropout和归一化等流行方法实际上增加了可塑性丧失（见扩展数据图4a）。另一方面，L2正则化在多种情况下减少了可塑性丧失（见图1、3和4中的紫线）。L2正则化通过在每一步将权重向零方向调整，阻止权重变得过大。较小的权重帮助网络保持可塑性。另一种减少可塑性丧失的现有方法是“缩减和扰动”（Shrink and Perturb）（见图1和图2中的橙线）。“缩减和扰动”是在L2正则化的基础上，对权重进行微小的随机变化。注入到网络中的这些变化可以减少单元的休眠，并增加表示的多样性（见图2和图4）。作者的结果表明，持续变化和非增长的权重可能对保持可塑性至关重要。

作者接下来描述一种反向传播算法的变体，该算法专门设计用于向网络注入变化并保持部分权重较小。传统的反向传播有两个主要部分：首先是用小的随机权重进行初始化，然后在每个训练步骤中进行梯度下降。虽然初始的随机权重提供了变化，但随着训练的持续，可塑性逐渐消失。为了维持变化，作者提出了一种新的算法——持续反向传播，在训练期间重新初始化少量单元，通常每步少于一个。为避免破坏网络已经学到的信息，作者仅重新初始化最少使用的单元。具体细节可见方法部分。

图1c中的蓝线显示了持续反向传播在持续ImageNet上的表现。该算法在持续ImageNet任务中显著减少了可塑性丧失，优于现有方法。同样，图2中的蓝线展示了持续反向传播在class-incremental CIFAR-100任务中的表现，以及对休眠单元和网络stable rank演变的影响。持续反向传播完全克服了可塑性丧失，保持了较高的stable rank，并且在整个学习过程中几乎没有单元休眠。

在强化学习中，持续反向传播与L2正则化结合使用（为防止对参数过度敏感，实验中仅加入少量正则化）。图3中的蓝线显示了PPO与持续反向传播在摩擦变化的Ant运动任务中的表现。PPO加上持续反向传播的表现远优于标准PPO，几乎没有可塑性丧失。在摩擦系数恒定的Ant运动任务中（见图4），PPO加上持续反向传播的表现在整个实验期间持续提升。图4b-d中的蓝线展示了使用持续反向传播时可塑性丧失相关指标的演变。PPO加上持续反向传播的网络中休眠单元较少，stable rank较高，平均权重幅度几乎保持不变。

研究结果支持以下观点：较小的权重有助于减少可塑性丧失，而持续注入变化可以进一步减轻这一问题。尽管“缩减和扰动”将变化施加于所有权重，但持续反向传播选择性地进行变化，这似乎更有助于保持网络的可塑性。

3.5 方法

持续反向传播的细节

持续反向传播会有选择性地重新初始化网络中效用（utility）较低的单元。作者使用的效用度量称为“贡献效用”（contribution utility），该度量针对每个连接（或权重）以及每个单元分别定义。贡献效用的核心直觉是，单元的激活值与其输出权重的乘积大小能够反映该连接对其下游单元的贡献程度。如果某个隐藏单元对下游单元的贡献较小，其作用可能会被其他隐藏单元的贡献掩盖。在这种情况下，该隐藏单元对整体网络的贡献较弱。作者将一个隐藏单元的贡献效用定义为其所有输出连接的效用之和。贡献效用通过瞬时贡献的运行平均值来进行度量，衰减率在所有实验中均设定为0.99。

在前馈神经网络中，第l层第i个隐藏单元在t时间的贡献效用 的更新公式为：

其中，是第l层第i个隐藏单元在t时间的输出，是连接第l层第i个单元与第l+1层第k个单元的权重，是第l+1层的单元数量。

当某个隐藏单元被重新初始化时，其输出权重会被重置为零。这种初始化方式确保新加入的单元不会干扰已经学到的功能。然而，将输出权重初始化为零会使新单元的效用值也为零，从而导致它容易在初始化后立即再次被重置。为避免这种情况，作者设定新单元在经过成熟阈值(maturity threshold) 次更新之前不会被重新初始化。当单元的更新次数超过时，作者称该单元为“成熟”单元。

在每一步训练中，每层中的成熟单元有一定比例 (替换率为 ) 会被重新初始化。替换率通常设定为一个非常小的值，意味着在数百次更新后才会替换一个单元。例如，在 class-incremental 的 CIFAR-100 任务中 (见图2)，作者使用的替换率为。该任务中网络的最后一层有 512 个单元，在每一步中，大约有个单元被替换。这相当于大约每更新次替换一个单元，或者在前五个类上大约每八个 epoch 替换一个单元。

最终的算法结合了传统的反向传播与选择性重新初始化，持续从初始分布中引入随机单元。持续反向传播在每次更新中都会执行梯度下降和选择性重新初始化步骤。算法1为前馈神经网络指定了持续反向传播的详细过程。当学习系统使用小批量数据时，可以通过对小批量数据的效用进行取平均值来替代保持运行平均值（running average），从而节省计算资源（详见扩展数据图5d中的示例）。持续反向传播克服了以往选择性重新初始化方法的局限性，并使其与现代深度学习兼容。

缓慢变化回归问题中不同激活函数引发的可塑性丧失

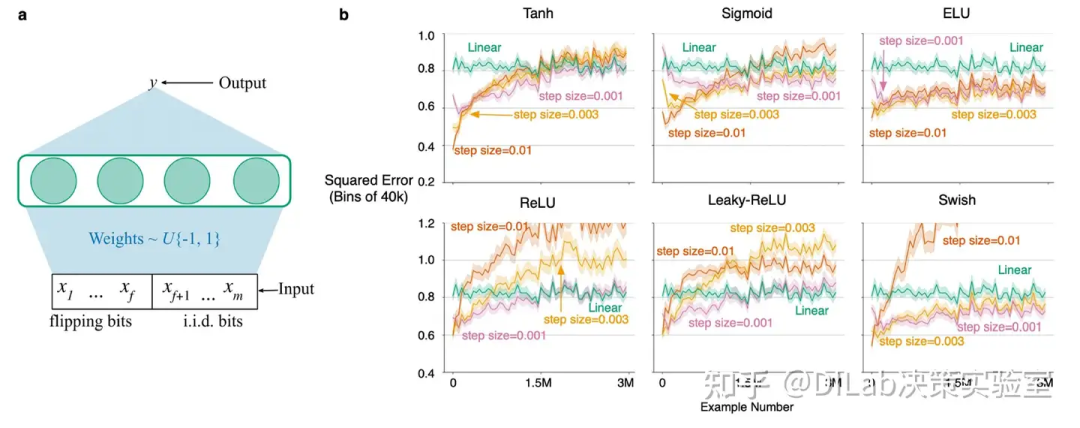(论文[3]-扩展数据图 2：缓慢变化回归问题中的塑性丧失。a，缓慢变化回归问题中的目标函数和输入。输入维度为 m + 1，每经过 T 个时间步会选取一位进行翻转，翻转其值。接下来的 m - f 位在每个时间步内是独立同分布的，最后一位固定为 1。目标函数由一个单隐层的LTU（线性阈值单元）神经网络表示，目标网络的每个权重取值为 -1 或 1。b，不同激活函数下的塑性丧失表现出稳健性。)

实验考察了六种常见激活函数（sigmoid、tanh、ELU、leaky ReLU、ReLU 和 Swish）的性能，重点分析了网络在长时间学习过程中的可塑性丧失现象。为确保实验的公平性，所有学习网络的权重均使用Kaiming初始化，并通过反向传播算法更新。实验过程中，作者提供了一致的样本序列以消除跨激活函数的随机性影响。结果表明，尽管所有激活函数在初期表现良好，但随着时间推移，不同程度的可塑性丧失逐渐显现。尤其是 ReLU和tanh激活函数的网络，误差迅速攀升，接近线性基准水平。其他激活函数如ELU虽表现稍好，但仍未能完全避免可塑性丧失。这表明常见的激活函数并不能有效解决可塑性丧失问题。

理解可塑性丧失

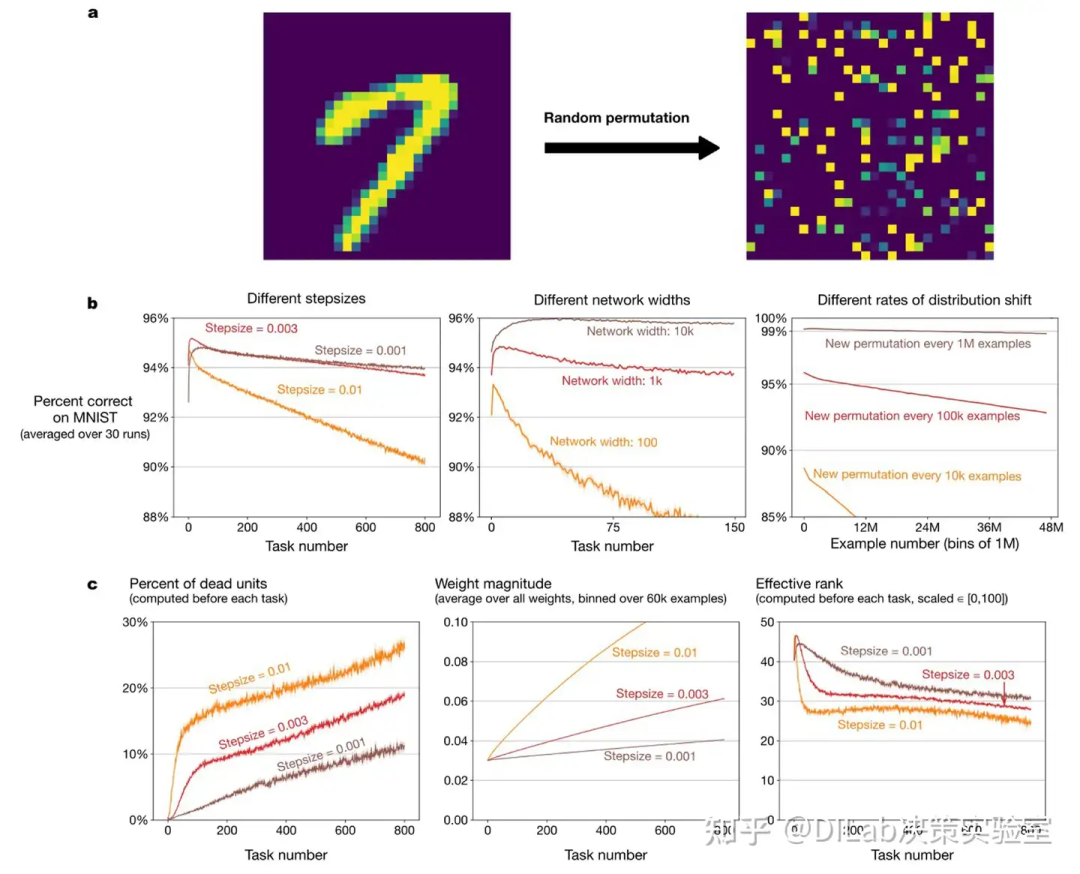(论文[3]-扩展数据图 3：在线置换 MNIST 实验中的塑性丧失。a，左图显示标签为“7”的 MNIST 图像，右图为对应的一种置换图像，对于MNIST数据集中的所有图像应用一种排列得到一个新的 permuted MNIST dataset，一共创建了800个 permuted MNIST datasets，每个 permuted MNIST datasets相当于一个新的 task，将这个新的问题称为 Online Permuted MNIST。b，在线置换 MNIST 实验中的塑性丧失在步长、网络规模和变化率上表现出稳健性。c，反向传播训练的深度网络在不同步长下的多种性质演变。左图显示网络中失效单元的百分比随时间增加。中图显示权重的平均幅值随时间增加。右图显示网络的有效秩随时间下降。)

现在，来探讨为何反向传播在持续学习问题中会导致可塑性逐渐丧失。学习者的唯一变化来源于网络权重的更新。最初，权重是从一个初始分布中随机采样得到的小幅随机数；然而，随着训练任务的增多，权重逐渐被优化，以适应最新的任务。因此，后续任务的初始权重与最初任务的初始权重在性质上出现了显著差异。由于学习算法的唯一变化体现在随时间调整的权重上，这表明初始权重分布具备某些特殊的性质，使得反向传播在早期阶段具有较高的可塑性。这种初始随机分布可能包含有助于可塑性的特性，例如单元的多样性、未饱和的单元状态以及权重的低幅度变化等。

随着可塑性的逐渐丧失，初始权重分布所带来的这些优势也随之减弱。每一种优势的流失在一定程度上解释了性能的下降。接下来，作者将详细讨论这些优势的丧失如何导致可塑性下降，并且提供了衡量各类现象发生频率的指标。作者通过对在线置换MNIST问题的深入研究，提出了几种可能缓解可塑性丧失的解决方案。

（1）可塑性丧失的第一个显著表现是恒定单元比例的持续增加。当一个单元变得恒定时，其梯度趋于零或完全为零，意味着该单元的输入权重将不再更新，导致该单元完全丧失可塑性。在ReLU激活函数中，当一个单元对任务中所有样本的输出都为零时，便会出现这种现象；此类单元通常被称为“死亡单元”。对于Sigmoid激活函数，当单元的输出接近激活函数的极值时，也会出现类似现象；此时的单元被称为“饱和单元”。

为了量化ReLU激活网络中死亡单元的数量，作者统计了每次新任务开始时，从随机抽取的2000个图像样本中，所有输出为零的单元数量。对于Sigmoid激活网络，类似的度量方法是统计输出接近激活函数极值的单元数量。在这一节中，作者主要关注了ReLU网络的表现。

在对在线置换MNIST问题的实验中，在线性能的下降伴随着死亡单元数量的显著增加（参见扩展数据图3c的左侧面板）。例如，在步长为0.01的情况下，经过800个任务后，多达25%的单元失活。由于置换MNIST问题中的输入数据均为正值（归一化至0到1之间），因此，一旦第一层的某个单元失活，它将永远保持失活状态。这种死亡单元的增加直接减少了网络的总容量。在接下来的章节中，作者将讨论防止单元死亡的策略，并展示这些策略如何显著延缓可塑性丧失。这进一步支持了死亡单元增加是反向传播中可塑性丧失的关键原因之一的结论。

（2）另一个随可塑性丧失而发生的现象是网络权重平均幅度的持续增长。作者通过将权重的绝对值相加并除以网络中权重的总数来计算权重的平均幅度。在置换MNIST实验中，扩展数据图3b显示，在线分类准确性的下降与权重平均幅度的增加密切相关（见扩展数据图3c的中间面板）。权重幅度的增长可能带来问题，因为较大的权重幅度通常与较慢的学习速度相关。神经网络中的权重与二阶泰勒展开中的Hessian矩阵的条件数直接相关。已知Hessian的条件数会影响随机梯度下降（SGD）算法的收敛速度。因此，权重幅度的增长可能导致Hessian矩阵条件数恶化，从而减缓算法收敛。

（3）最后一个与可塑性丧失相关的现象是表征的有效秩下降。矩阵的秩表示其线性独立维度的数量，而有效秩则衡量每个维度对该矩阵变换的影响程度。高有效秩表明矩阵的多数维度对变换有相似的贡献；相反，低有效秩意味着大多数维度对变换的贡献很小，信息冗余较多。

考虑一个矩阵，其奇异值为，，。令，其中是包含所有奇异值的向量，表示范数。矩阵的有效秩 (effective rank, erank()) 定义为：

其中

有效秩是一个连续的度量，取值范围在1到矩阵的秩之间。

实验结果表明，网络可塑性的丧失伴随着网络平均有效秩的下降（见扩展数据图3c右侧面板）。这一现象本身并不必然构成问题。实际上，已有研究指出，基于梯度的优化过程往往通过隐式正则化，倾向于选择低秩解。这种隐式最小化秩的过程有助于优化的稳定性。然而，低秩解在应对新任务时可能带来不利影响，因为它限制了隐藏单元提供的信息量，从而削弱了模型从新任务中学习的能力。有效秩的下降为作者实验中观察到的可塑性丧失现象提供了合理的解释。在每个任务完成后，学习算法会找到当前任务的低秩解，并将其作为下一个任务的初始状态。随着任务的累积，表示层的有效秩逐渐下降，导致模型在新任务时可表示解的空间受到限制。

在本节中，作者深入探讨了在线置换MNIST问题中网络可塑性丧失的成因。研究发现，随着时间推移，学习算法的唯一变化在于网络权重的更新，而这表明初始权重分布的某些特性赋予了算法初期的可塑性。随着训练过程的推进，网络权重逐渐偏离其初始分布，导致算法的可塑性逐渐丧失。作者进一步发现，可塑性的丧失与以下三个现象密切相关：权重幅度的增加、表征有效秩的下降以及死亡单元比例的上升。每个现象都在一定程度上解释了反向传播过程中可塑性丧失的机制。

现有的缓解可塑性丧失的深度学习方法

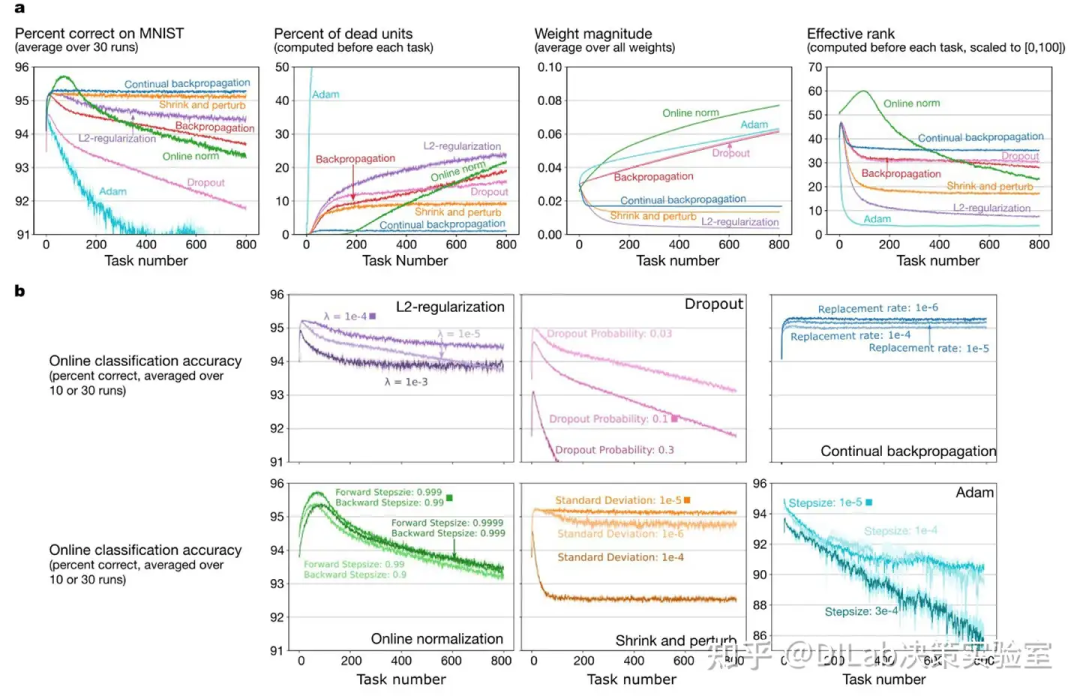(论文[3]-扩展数据图 4：不同深度学习方法在在线置换 MNIST 上的表现。

a，左图展示了不同算法在在线置换 MNIST 上的在线分类准确率。Shrink and Perturb 算法的准确率几乎没有下降。持续反向传播算法没有表现出塑性丧失，并且取得了最佳性能。中左图显示，除持续反向传播外，所有方法的失效单元百分比随时间增加；持续反向传播在整个训练过程中几乎没有产生失效单元。中右图显示，除 L2 正则化、Shrink and Perturb 和持续反向传播外，所有方法的权重平均幅值均随时间增加。这三种方法在实验中表现最佳，表明小幅权重对于快速学习至关重要。右图展示了所有方法的有效秩随时间下降。然而，持续反向传播保持了比反向传播和 Shrink and Perturb 更高的有效秩。在所有算法中，只有持续反向传播同时保持了较高的有效秩、较低的权重幅值以及较低的失效单元百分比。b，针对在线置换 MNIST，不同算法在不同超参数组合下的表现。每种方法展示了三种不同的超参数设置。)

在本节中，作者探索了几种现有方法对神经网络可塑性丧失的影响，并选择了五种方法进行实验：L2正则化、Dropout、在线归一化、Shrink and Perturb 以及 Adam。这些方法中，L2正则化、Dropout、在线归一化和Adam是深度学习中常见的技术，而 Shrink and Perturb 虽然不常用，但由于它能缓解预训练失败问题，成为本研究的一个重要参考。为了评估这些方法的效果，作者在在线随机排列的MNIST任务上进行了实验，使用了前一节中相同的网络架构和评价指标，并统一了步长参数（0.003）以确保实验结果的可比性。

L2正则化通过对网络权重的二范数施加惩罚，限制了权重幅度的增长，部分缓解了可塑性丧失。然而，它并未完全解决问题，尤其是在死单元百分比和有效秩方面。Shrink and Perturb通过收缩权重并添加噪声，进一步减少了可塑性丧失，尤其是在死单元的控制上表现出色，但其有效秩仍低于反向传播。此外，该方法对噪声标准差较为敏感，过高或过低的噪声都会影响效果。

Dropout作为一种常用的正则化方法，未能有效缓解可塑性丧失，甚至在某些情况下加剧了问题。不同的Dropout概率对网络的影响差异显著，较高的概率导致更为严重的可塑性丧失。在线归一化在初期任务中表现较好，但随着时间推移，其性能迅速下降，表现为死单元的增多和有效秩的降低。

Adam优化器尽管在深度学习中广泛使用，但在本研究中表现尤为糟糕。Adam显著加剧了可塑性丧失，导致大量死单元和有效秩的剧烈下降。这一发现对深度强化学习具有重要意义，因为Adam在该领域是常用的优化器，而持续学习的环境要求较高的网络可塑性。

在所有测试的方法中，Shrink and Perturb和L2正则化在减少可塑性丧失方面表现相对较好，但它们对超参数的选择较为敏感。相比之下，持续反向传播通过动态替换死单元并引入适量随机性，表现出最为稳定和优异的结果，成功缓解了可塑性丧失的所有相关指标，并在不同任务中保持了较高的有效秩。

强化学习的细节与进一步分析

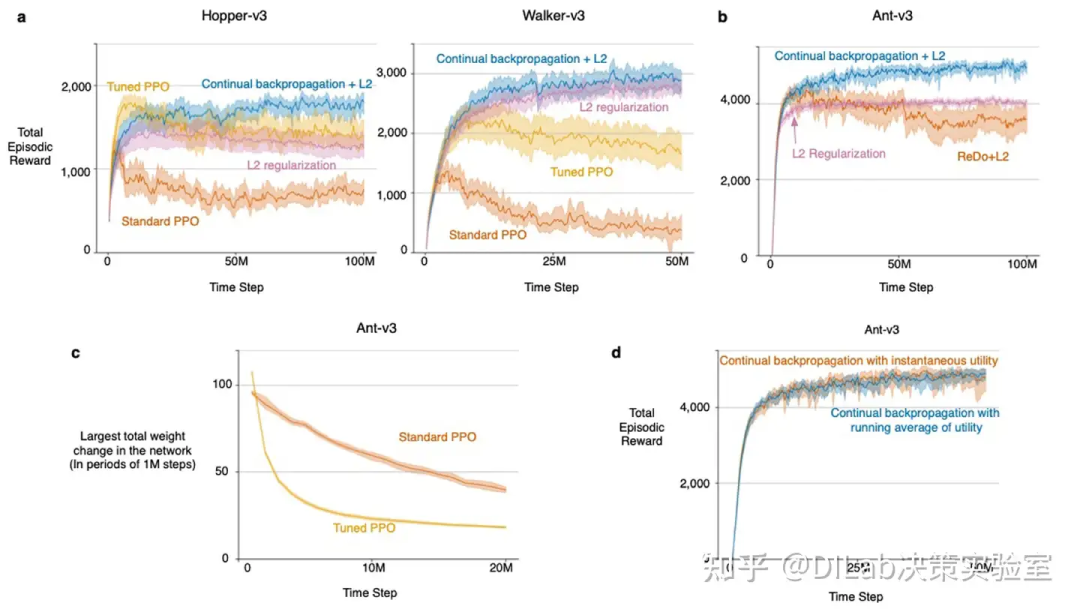(论文[3]-扩展数据图 5：平稳强化学习问题中的进一步结果（即摩擦系数不变）。a，如图 4 所示，标准 PPO 的性能随时间下降。然而，与图 4 不同的是，在 Hopper-v3 中，PPO 加入 L2 正则化后其性能随时间下降更为明显。另一方面，结合持续反向传播和 L2 正则化的 PPO 能够随着时间推移不断改进性能。b，持续反向传播与 ReDo 在 Ant-v3 上的比较。ReDo 和 L2 正则化的 PPO 性能随时间下降，而持续反向传播结合 L2 正则化的 PPO 性能则随着时间推移不断提升。c，使用标准 Adam 优化的 PPO 导致策略网络的大幅更新，而使用正确参数（β1 = β2 = 0.99）的 Adam 则不会，这解释了为什么正确 Adam 下的 PPO 表现优于标准 PPO。d，持续反向传播的两种效用形式的比较：一种基于瞬时效用的运行估计，另一种仅使用瞬时效用。两种方法的性能相似。)

本文中的实验在 OpenAI Gym 的 Ant-v3 环境中进行。作者通过对摩擦系数从[0.02, 2.00]范围内进行以10为底的对数均匀采样，改变了摩擦系数。摩擦系数在首次 episode 边界发生变化后，经过200万步才被调整。此外，作者在该问题上测试了Shrink and Perturb方法，结果表明相比L2正则化，它并未带来显著的性能提升。策略网络和价值函数网络分别由两个独立的网络组成，每个网络包含两层隐藏层，每层有256个单元。作者使用Adam优化器结合PPO算法来更新网络权重，其他超参数的详细设置请参见扩展数据表5。所有强化学习实验结果图中的阴影区域表示95%的自举置信区间。

在Ant环境中，奖励信号由四个部分组成。主要部分奖励智能体的向前移动，与 Ant 在上一步中沿正x方向移动的距离成正比。第二部分为时间步奖励，每个时间步固定奖励1。第三部分惩罚智能体执行大幅度动作，其值与动作幅度的平方成正比。最后一部分惩罚智能体产生较大的外部接触力，该项与剪裁后的外力总和成正比。每个时间步的奖励信号是这四个部分的加和。

实验显示，PPO结合L2正则化在较高的权重衰减值（如）时能够避免性能退化，但过大的权重衰减会阻止智能体找到更优策略，导致其停留在次优解。通过结合持续反向传播与L2正则化，PPO在各个环境中的性能得到了显著改善，尤其是在Walker-v3和Hopper-v3环境中的表现与Ant-v3相似。使用较小的权重衰减值（）和替换率能够减少性能退化，提升学习稳定性。

所有结合持续反向传播和L2正则化的PPO实验均使用了的权重衰减，的替换率和的成熟度阈值。作者发现，PPO结合持续反向传播和L2正则化的性能对替换率敏感，但对成熟度阈值和权重衰减不敏感。

PPO使用Adam优化器，该优化器对梯度及其平方保持运行估计。这些估计需要两个额外的参数，分别是和。标准的和值为0.9和0.999，作者称之为标准Adam。Lyle等人的研究表明，使用标准的和会导致显著的可塑性丧失，原因在于和之间的差异。当突然出现较大梯度时，由于较大，与梯度平方相关的运行估计（用于分母）更新速度远慢于梯度（用于分子），导致较大的更新。将设为等于可以减少Adam中的可塑性丧失。此外，作者调整了Adam优化器的参数，将和均设为0.99，以减少PPO结合标准Adam造成的可塑性丧失，称之为调整后的PPO。在实验中，调整后的Adam显著降低了权重更新的幅度，稳定了学习过程。

作者还对 ReDo 方法（ReDo 也可以看做是一种基于持续反向传播的选择性重新初始化方法，但其效用度量和重新初始化策略与本文不同。）进行了初步评估，表明其结合 PPO 在 Ant-v3 环境中的性能有所提升，但仍存在一定的性能退化，深入对比，作者留作未来研究。值得注意的是，PPO 的性能退化现象与可塑性丧失和遗忘密切相关。通过使用小型回放缓冲区，本文进一步揭示了深度强化学习中可塑性丧失的问题，并为未来研究提供了新的视角，尤其是在面对非平稳环境时如何保持智能体的学习能力。

3.6 讨论

持续学习的两个核心目标是保持稳定性与可塑性。稳定性指的是系统能够记住有用的信息，而可塑性则是系统在面对变化的数据分布时，能够持续发现新的有用信息。现有的深度学习方法在保持稳定性方面面临挑战，尤其容易遗忘先前的知识。许多研究集中于解决稳定性问题，而本文的研究重点在于如何保持可塑性。研究发现，当前反向传播机制未能有效解决遗忘问题，其主要原因在于现有的效用度量仅关注单元对当前数据的重要性，忽视了长期效用的衡量。未来研究应致力于开发能够兼顾稳定性与可塑性的方法，以更好地应对持续学习中的挑战。

理想的持续学习系统不仅应能够持续学习新知识，还应在记忆与遗忘之间取得平衡，并且具备高效的计算与内存利用率。不同的基准任务对系统的能力测试侧重点不同。例如，Continual ImageNet适合研究可塑性，而class-incremental CIFAR-100则能够测试系统利用过往知识加速学习的能力。克服可塑性丧失是实现快速学习未来数据的关键一步，然而这只是初步阶段，后续还需研究如何利用已有知识更高效地学习新任务。

研究表明，随着任务数量的增加，深度学习系统的可塑性逐渐丧失，这在多任务学习中尤为明显。例如，在class-incremental CIFAR-100中，系统在学习100个类后表现明显下滑。尽管如此，目前对于哪些初始化属性有助于保持可塑性仍然缺乏深入理解，这将是未来研究的一个重要方向。此外，如何区分系统失去优化新目标能力与失去泛化能力的两种可塑性丧失现象也是一个尚待解决的问题。

持续反向传播通过效用度量识别并替换低效用单元，但其效用度量仍基于启发式方法，未来的研究应探索更系统的效用度量。此外，持续反向传播与神经网络修剪中的效用度量密切相关，结合这两者可能为开发新算法提供新的思路。动态稀疏训练与持续反向传播在应对可塑性丧失中也展现出潜力，尤其是在高稀疏度下，其性能接近稠密网络，未来可能在持续学习中发挥更大作用。

持续学习中的一个常见策略是增加网络的单元，但这往往伴随内存需求的无限增长。与此相反，本文提出的持续反向传播方法在有限内存条件下，通过选择性地重新初始化低效用单元，避免了内存的无限扩展需求。此外，完全重新初始化网络虽在某些情境下表现良好，但在任务数量多且无缓冲区的强化学习系统中，其效果有限，甚至可能导致系统遗忘所有已学内容。

可塑性丧失可能与彩票假设有关，即在随机初始化的网络中存在少量“中奖票”可以通过少量更新达到良好性能。研究发现，随着任务的增加，网络中的有效表示维度减少，可能意味着“中奖票”数量的减少，这为未来研究可塑性丧失提供了一个新的视角。持续学习中的噪声注入与小权重幅度的保持也被证明能够有效减少可塑性丧失，尤其是在非平稳数据流的情况下，这种方法通过结合L2正则化展现了保持可塑性的潜力。

总之，本文强调了在持续学习中保持可塑性的重要性，并提出了一些可能的解决方案和未来研究方向，包括基于更系统的效用度量、动态稀疏训练以及对可塑性丧失与彩票假设之间关系的进一步探讨。

4. 总结与展望

本文围绕深度强化学习中的重放比率与网络可塑性，对三项代表性研究进行了分析与讨论。

首先，“休眠神经元”现象表明高重放比率可能导致网络中大量神经元变为休眠状态，削弱网络的表达能力。针对这一问题，ReDo 方法通过循环利用休眠神经元，成功维持了网络的可塑性，提升了模型性能。

其次，BBF Agent 的研究显示，在样本受限的条件下，适当扩大网络规模并结合高重放比率与周期性重置机制，可以显著提升模型性能。该工作强调了网络规模、重放比率与可塑性之间的平衡，以及训练策略对模型性能的关键作用。

最后，持续学习中的可塑性丧失指出，深度学习网络在持续学习环境中会逐渐失去可塑性，影响新知识的学习。通过持续反向传播等方法，引入网络结构的多样性，有助于维持可塑性，促进持续学习的效果。

综合以上分析，我们可以得出以下结论：

重放比率的影响：高重放比率虽然有助于提高学习效率，但可能导致网络可塑性下降，需要通过方法如 ReDo 或网络重置来缓解负面影响。
网络规模的平衡：扩大网络规模可以提升模型性能，但在数据量有限的情况下，需要配合有效的训练策略以充分发挥大规模网络的优势，避免过拟合和计算资源浪费。
可塑性的维持：在持续学习和强化学习中，保持网络的可塑性至关重要。引入多样性和适当的正则化方法，如持续反向传播和权重衰减，有助于防止可塑性丧失。未来的研究应致力于综合考虑网络规模、重放比率和可塑性等因素，建立更有效、更稳健的深度强化学习模型。这将有助于推动人工智能在更广泛领域的应用和发展，实现智能体在复杂、多变环境中的持续学习和适应能力。

5. 参考文献

[1] Sokar, Ghada, et al: "The dormant neuron phenomenon in deep reinforcement learning." International Conference on Machine Learning: PMLR, 2023.

[2] Schwarzer, Max, et al: "Bigger, better, faster: Human-level atari with human-level efficiency." International Conference on Machine Learning: PMLR, 2023.

[3] Dohare, Shibhansh, et al: "Loss of plasticity in deep continual learning." Nature 632.8026 (2024): 768-774.