问题：
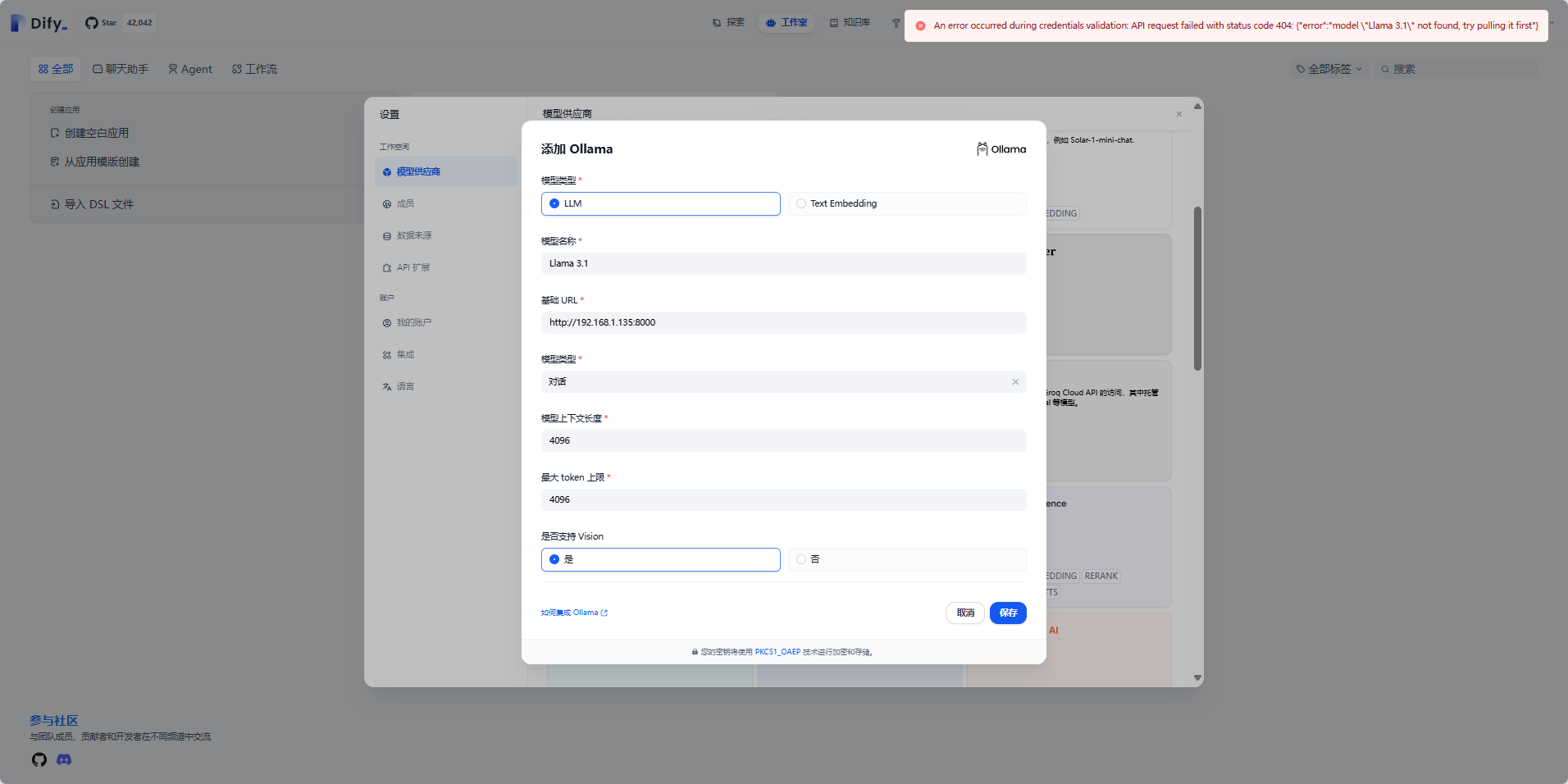
这周使用Flask框架写了一个数据展示的小网页，在发布的时候发现构建失败，查看日志发现是这次新增的一个第三方库没有安装到服务端，导致构建的时候失败了
解决问题：
服务端发布新增第三方库
解决过程
1、确定服务器连接工具Termius
查看同事之前写的发布过程，发现需要使用一个服务器连接工具，之前同事用的是MobaXterm
,但是这个没有Mac版本，经过调研发现了另外一个工具，Appstore里中就可以下载
Termius是一款远程访问和管理工具,旨在帮助用户轻松地远程连接到各种服务器和设备。
2、Termius中连接服务器
下载完成后，使用邮箱注册，登陆即可
配置要连接的服务器
开始连接
连接成功
3、服务器端安装
ls命令：打印出所有文件目录
cd命令：进入指定文件夹
cd命令经常与ls命令组合使用，最终达到进入指定文件的作用，最后进入到自己的工具项目
进入到自己项目后，需要先创建虚拟环境
wxqas-Mac-mini-6:yating_tools wxqa$ virtualenv --python /usr/local/bin/python3 venv
接着，激活虚拟环境
wxqas-Mac-mini-6:yating_tools wxqa$ source /Users/wxqa/Jenkins/Home/workspace/yating_tools/venv/bin/activate
注意：和别人给的命令不一样（可能是mac版本和别的不一样）
激活以后，后面的操作环境前都会带着venv的标识
接着，重新安装requirement文件
然后，发现有报错，有个库的版本不合适，然后构建还是失败
然后就修改requirements文件，添加另一个库名
再进行服务器端安装，发现有报错，查找了一些方法，解决不了，决定换一个数据库操作的第三方库
解决方法：更换为pymysql库，这个服务端已经安装的有，按照这个语法进行替换原来的SQL语句
就可以了
