2024-10-03, 英国诺丁汉大学数学科学学院的Gary R. Mirams教授团队创建了一个基于英国地形的二维优化基准数据集,该数据集包含了经过修改的英国地形数据,并从中识别出了957,174个局部最优解,为优化算法的评估提供了新的视角。
一、研究背景:
在优化算法领域,真实世界的复杂性一直是评估算法性能的挑战。随着优化算法在各个领域的广泛应用,如何评估和比较这些算法的性能成为了一个重要课题。传统的人工合成基准数据集虽然在一定程度上有助于算法性能的评估,但它们往往无法充分反映现实世界问题的复杂性和多样性。
目前遇到的困难和挑战 :
现有的优化算法基准测试主要面临两大挑战:
一、基准数据集往往过于简化,无法真实反映现实世界问题的复杂性;
二、缺乏足够多的局部最优解,导致算法的全局搜索能力无法得到充分测试。
数据集地址:OS Terrain 50|地形数据数据集|优化算法数据集
二、让我们一起来看一下 数据集
基于英国地形数据,通过线性插值方法生成了一个具有957,174个局部最优解的目标函数,用于评估优化算法的性能。使用了英国地形50(UK Ordnance Survey Terrain 50)数据集,通过对原始数据的轻微修改和线性插值,模拟出了英国地形的数据集
数据集特点:
1、包含957,174个局部最优解
2、真实世界的地形数据提供了一个复杂且具有挑战性的测试平台
3、通过离散方法对局部最优解及其吸引盆进行了分类和识别
数据集使用方法:
数据集通过Python模块nevis提供,支持线性插值查询,并提供了可视化和算法性能评估工具。
基准测试 :
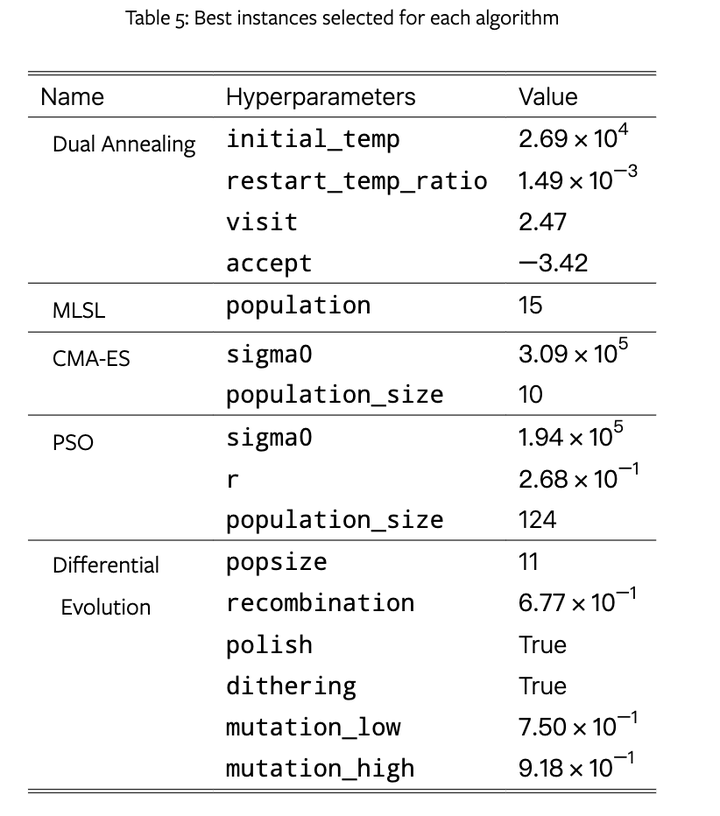
研究团队开发了一个基于该数据集的基准测试框架,提出了一种新的性能度量方法——广义预期运行时间(Generalized Expected Running Time, GERT),并使用optuna框架进行超参数调整。
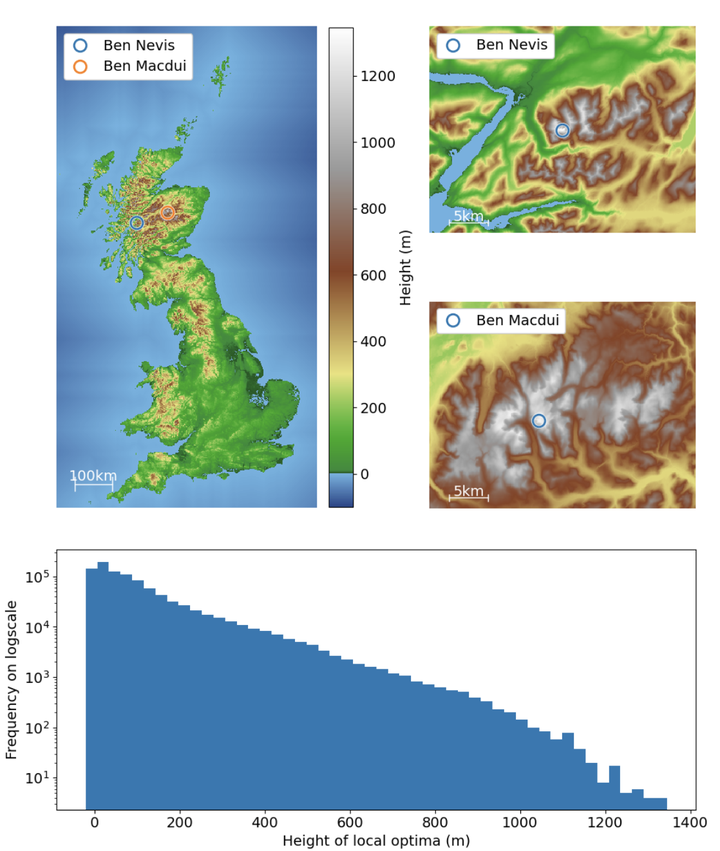
英国地形数据改编自地形测量局“OS Terrain 50”数据集。显示了一个 700 公里 x 1300 公里的矩形,包括英国及其岛屿的陆地面积,但省略了附近的爱尔兰和法国陆地,以及算法生成的海底高程水平(见正文)。插图以相同的比例显示了两座最高峰(本尼维斯第一峰和本麦克杜伊第二峰)周围的区域。
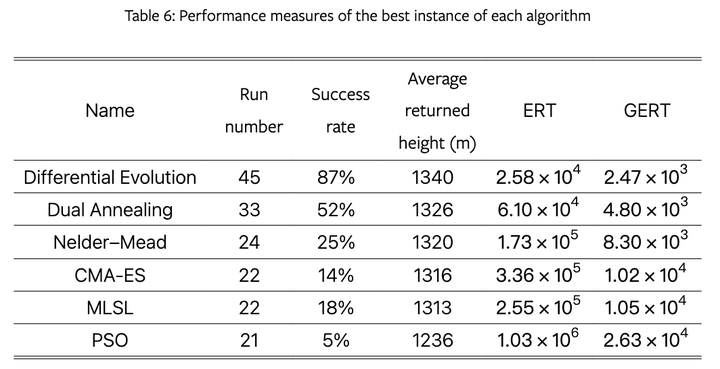

每个算法的选定实例的聚合收敛图。在左侧的每个聚合收敛图中, 𝑥 -axis 表示函数评估的次数,线条显示每次函数评估时所有运行中到目前为止的最佳高度的平均值和五个数字摘要。对于在最大函数计算数之前终止的运行,到目前为止的最佳高度是 “padded”。
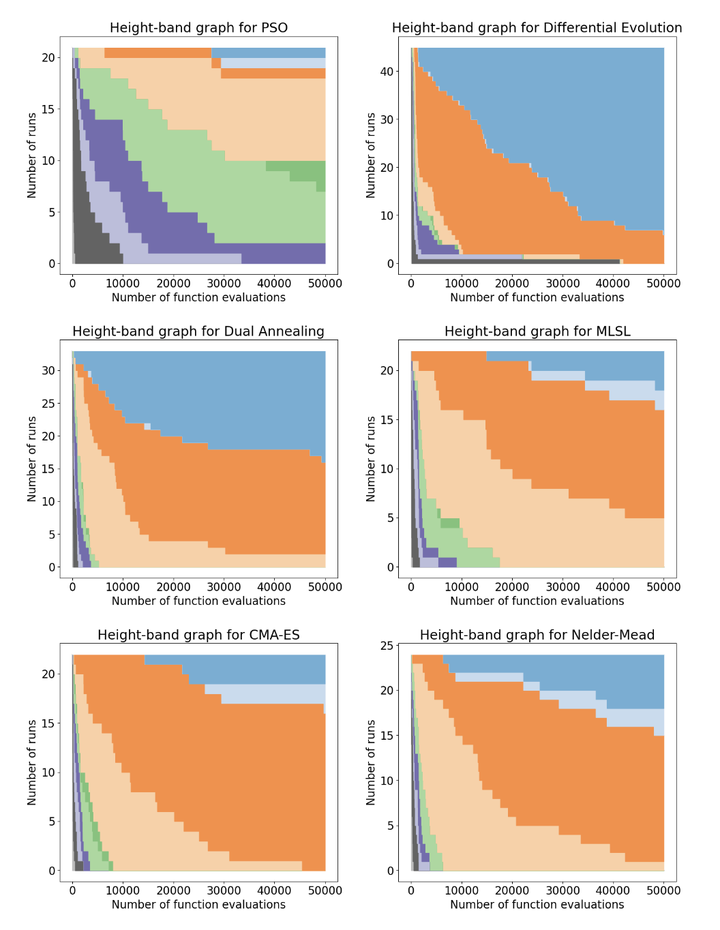
每种算法的选定实例的高度带图。每个高度带图显示了在每种函数计算次数的所有运行中预定义高度带(表 1)内的最佳到目前为止的高度分布。对于在最大函数计算数之前终止的运行,到目前为止的最佳高度是 “padded”。每个图形的深蓝色 (Ben Nevis) 区域是填充过程的结果
三、 数据集应用场景:
比如,我是一名计算机科学系的教授,我正在教授一门关于优化算法的课程。我想要向学生展示这些算法是如何在复杂的环境中寻找最优解的。我决定使用这个基于英国地形的数据集来进行演示。
本次教学的目标:
我希望通过这个案例,让学生理解以下几点:
-
什么是局部最优解和全局最优解。
-
不同的优化算法是如何应对复杂的地形。
-
算法在实际应用中可能遇到的挑战。
教学步骤
步骤一:引入问题 我首先向学生解释,假设他们正在参与一场登山比赛,目标是找到英国的最高峰——本尼维斯峰。但是,他们只能通过一系列的海拔数据来推测自己的路径,而且他们可能会遇到很多误导人的山峰(局部最优解)。
步骤二:展示数据集 我打开了一个交互式的地图,展示了英国的地形。我给学生展示,这个地图不仅仅是一张图,它实际上是一个由数学函数生成的复杂地形模型,包含了成千上万的山峰和山谷。
步骤三:运行优化算法 接着,我选择了一个优化算法,比如遗传算法,并在课堂上实时运行它。我解释了算法的工作原理,并指出它如何根据当前位置的海拔高度来决定下一步的移动方向。
步骤四:观察算法表现 随着算法的运行,学生们可以看到算法在地图上的移动轨迹。一开始,算法可能会被一些较高的局部最优解所吸引,比如到达了本尼维斯峰附近的一些山峰。我指出,这些就是算法在寻找全局最优解过程中可能遇到的陷阱。
步骤五:讨论算法决策 我引导学生讨论算法为什么会被局部最优解所吸引,以及如何改进算法来避免这种情况。学生们提出了一些想法,比如增加随机性、使用更复杂的决策规则等。
步骤六:比较不同算法 我接着展示了几种不同的优化算法在同一个任务上的表现,包括它们是如何被局部最优解所迷惑,以及它们是如何成功找到本尼维斯峰的。学生们可以看到,不同的算法在面对复杂地形时有不同的策略和表现。
步骤七:总结讨论 最后,我总结了这次演示,强调了优化算法在实际应用中可能遇到的挑战,以及如何通过理解算法的工作原理和调整参数来提高算法的性能。
通过展示了如何将抽象的优化算法概念与实际的地形数据相结合,学生们不仅理解了优化算法的理论知识,还直观地看到了算法在实际应用中的表现。可以让学生能够在一个有趣且具有挑战性的场景中学习和理解这些算法。
知识小课堂:
在优化问题中,局部最优解(Local Optima)是指在某个问题的解空间中的一个点,在其邻域内没有比它更优的解。换句话说,如果你从这个点开始在解空间中搜索,你找不到比它更好的解。但是,局部最优解不一定是全局最优解(Global Optima),也就是在整个解空间中最好的解。
例如,如果我们考虑一个地形图,局部最优解可以想象为一个山谷或小山丘的最高点,站在这个点上,四周都是下坡,也就是说在邻近的区域内,你找不到比这个点更高的点。然而,在更远的地方可能存在更高的山峰,这些更高的山峰就是全局最优解。
在这篇文章中,研究者们通过分析英国地形数据集,识别出了957,174个这样的局部最优解。
这些局部最优解对于测试优化算法的性能非常有用,因为它们可以模拟出算法在复杂地形中寻找最高点(全局最优解)时可能遇到的困难。如果一个优化算法能够成功地找到避开这些局部最优解并找到真正的最高点的路径,那么这个算法就被认为具有很好的全局搜索能力。