数学建模算法与应用第9章支持向量机及其方法

news2024/10/11 7:59:44

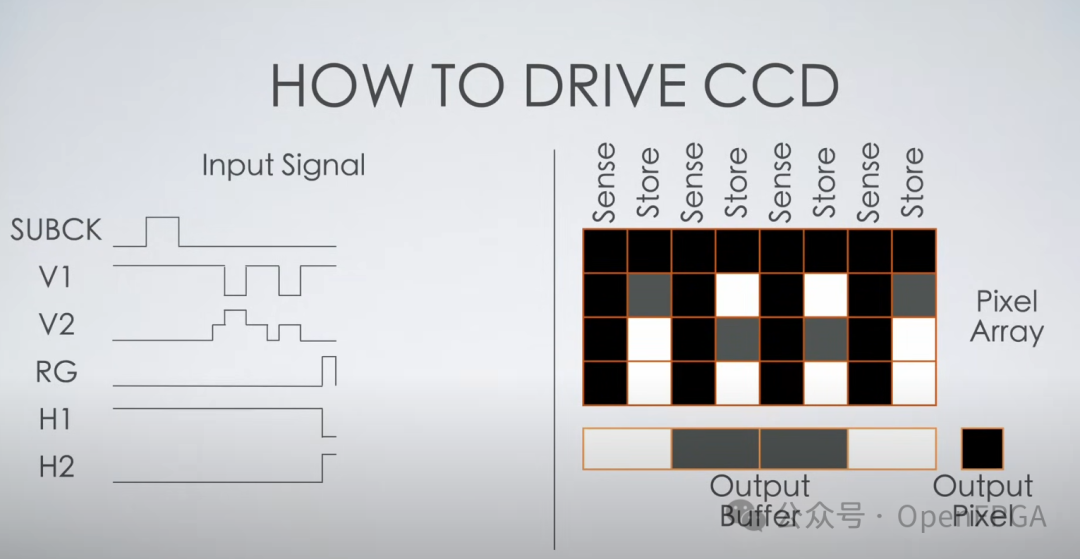
9.1 支持向量机的基本原理

核函数的种类：

9.2 支持向量机的Matlab命令及应用

Matlab代码示例：二分类支持向量机

9.3 乳腺癌的诊断案例

Matlab代码示例：乳腺癌数据分类

9.4 支持向量回归（SVR）

Matlab代码示例：支持向量回归

习题 9

总结

支持向量机（Support Vector Machine, SVM）是一种监督学习方法，广泛应用于分类和回归分析中。它通过寻找最优分隔超平面来最大化类别之间的间隔，是一种强大且高效的机器学习算法。本章将介绍支持向量机的基本概念、分类与回归的原理，以及在Matlab中的实现方法。

9.1 支持向量机的基本原理

支持向量机的基本思想是通过找到一个最优超平面来将数据进行分离。对于线性可分的情况，支持向量机找到使得两类之间间隔最大的超平面。而对于线性不可分的情况，SVM通过引入核函数将数据映射到更高维的特征空间，使其在高维空间中可分。

最优超平面：通过最大化不同类别之间的间隔来找到最优分隔边界，这个边界是由离超平面最近的点（支持向量）决定的。
核函数：当数据在原始空间中不可分时，可以使用核函数将其映射到高维空间。常用的核函数包括线性核、RBF核、多项式核等。

核函数的种类：

线性核（Linear Kernel）：适用于线性可分的数据，计算速度快。
高斯径向基函数核（RBF Kernel）：适用于大多数非线性可分的数据，具有很强的表达能力。
多项式核（Polynomial Kernel）：适用于具有多项式关系的数据。

核函数	描述	应用场景
线性核	用于线性可分问题	文本分类、简单分类任务
RBF核	处理非线性关系	图像识别、复杂数据分类
多项式核	表达多项式特性	特征之间存在多项式关系的情况

9.2 支持向量机的Matlab命令及应用

Matlab中提供了支持向量机的相关工具箱，可以用于分类和回归任务。主要函数包括fitcsvm、predict等。

Matlab代码示例：二分类支持向量机

% 生成样本数据
X = [randn(50, 2) + 2; randn(50, 2) - 2];  % 两类数据
Y = [ones(50, 1); -ones(50, 1)];

% 使用线性核函数训练支持向量机模型
SVMModel = fitcsvm(X, Y, 'KernelFunction', 'linear');

% 绘制支持向量机的决策边界
figure;
gscatter(X(:,1), X(:,2), Y);
hold on;
plot(SVMModel.SupportVectors(:,1), SVMModel.SupportVectors(:,2), 'ko', 'MarkerSize', 8);

% 绘制决策边界
d = 0.02;
[x1Grid, x2Grid] = meshgrid(min(X(:,1)):d:max(X(:,1)), min(X(:,2)):d:max(X(:,2)));
XGrid = [x1Grid(:), x2Grid(:)];
[~, scores] = predict(SVMModel, XGrid);
contour(x1Grid, x2Grid, reshape(scores(:,2), size(x1Grid)), [0 0], 'k');
hold off;
xlabel('特征1');
ylabel('特征2');
title('二分类支持向量机');

在上述代码中，生成了两类数据并使用线性核的支持向量机进行分类。fitcsvm函数用于训练支持向量机模型，最后绘制了分类边界和支持向量。

9.3 乳腺癌的诊断案例

支持向量机在医学诊断中也有广泛应用，例如通过分析病人的数据来诊断乳腺癌。通过将病人的特征数据输入支持向量机模型，可以得到该病人是否患有乳腺癌的预测结果。

Matlab代码示例：乳腺癌数据分类

% 加载乳腺癌数据
load fisheriris;
X = meas(51:end, 3:4);  % 选择两类数据和两个特征
Y = species(51:end);

% 训练支持向量机分类器
SVMModel = fitcsvm(X, Y, 'KernelFunction', 'rbf', 'Standardize', true);

% 进行交叉验证
CVSVMModel = crossval(SVMModel);
classLoss = kfoldLoss(CVSVMModel);

% 输出分类误差
fprintf('分类误差为：%.3f\n', classLoss);

上述代码使用了fisheriris数据集中的部分数据对支持向量机进行训练，并使用RBF核函数对数据进行分类，同时进行了交叉验证以评估模型的准确性。

9.4 支持向量回归（SVR）

除了分类任务，支持向量机还可以用于回归分析，称为支持向量回归（SVR）。SVR的目标是找到一个函数来逼近数据，保证误差在一定范围内最小化，同时控制模型的复杂度。

Matlab代码示例：支持向量回归

% 生成样本数据
x = (1:100)';
y = sin(x / 10) + 0.1 * randn(100, 1);

% 使用支持向量回归进行拟合
SVRModel = fitrsvm(x, y, 'KernelFunction', 'rbf');

% 进行预测
x_test = (1:0.1:100)';
y_pred = predict(SVRModel, x_test);

% 绘制结果
figure;
plot(x, y, 'b.', 'MarkerSize', 15);
hold on;
plot(x_test, y_pred, 'r-');
xlabel('自变量 x');
ylabel('因变量 y');
title('支持向量回归分析');
legend('原始数据', '回归曲线');
hold off;

该代码展示了如何使用支持向量回归对数据进行拟合，生成了含有噪声的正弦数据，并使用RBF核的SVR进行拟合分析。

习题 9

在第九章结束后，提供了一些相关的习题，帮助读者深入理解支持向量机的基本原理及其应用。习题9包括：

二分类问题：使用支持向量机对给定的两类数据进行分类，选择不同的核函数进行对比。
乳腺癌诊断模型：使用公开数据集训练一个支持向量机模型，对乳腺癌进行分类预测，并评估模型的性能。
支持向量回归：对一组非线性数据使用支持向量回归进行拟合，并比较不同核函数的拟合效果。

通过这些习题，读者可以进一步掌握支持向量机在分类与回归中的应用，以及如何利用Matlab工具实现支持向量机方法。

总结

第九章介绍了支持向量机的基本概念及其应用，包括分类任务的支持向量机（SVM）和回归任务的支持向量回归（SVR）。支持向量机通过最大化分类间隔寻找最优超平面，是一种非常强大的分类和回归工具。通过核函数，SVM能够处理线性不可分的数据，广泛应用于文本分类、图像识别和医学诊断等领域。通过本章的学习，读者可以掌握支持向量机的基本原理和方法，并利用Matlab进行SVM的分类与回归建模。