今天带来一期轨迹跟踪算法的讲解,首先讲解二维平面中的导航向量场[1]。该方法具有轻量化、计算简便、收敛性强等多项优点。该方法根据期望的轨迹函数,计算全局位置的期望飞行向量,将期望飞行向量转为偏光角,输入底层控制器,即可导引被控对象不断跟踪至期望轨迹。该方法适用于非全约束的移动机器人,如固定翼无人机、独轮车、小车(非全向麦克纳姆轮式)、船舶等。对于全约束的移动机器人,如四旋翼无人机、麦克纳姆轮式小车,仅控制前进方向和偏航方向,也是同样可以使用的。
在本期文章中,主要讲解向量场计算方式和使用,机器人根据向量场给出的方向最终会收敛至期望轨迹的相关证明过程可以参考原始论文。
轨迹表达式
考虑以(0,0)为圆心,
r
=
10
r=10
r=10为半径的期望圆轨迹,有如下轨迹方程:
x
2
+
y
2
=
100
x^2+y^2=100
x2+y2=100
对上式等式两边开平方,移到一边,得到如下函数
φ
(
x
,
y
)
\varphi(x,y)
φ(x,y):
φ
(
x
,
y
)
=
x
2
+
y
2
−
10
\varphi(x,y)=\sqrt{x^2+y^2}-10
φ(x,y)=x2+y2−10
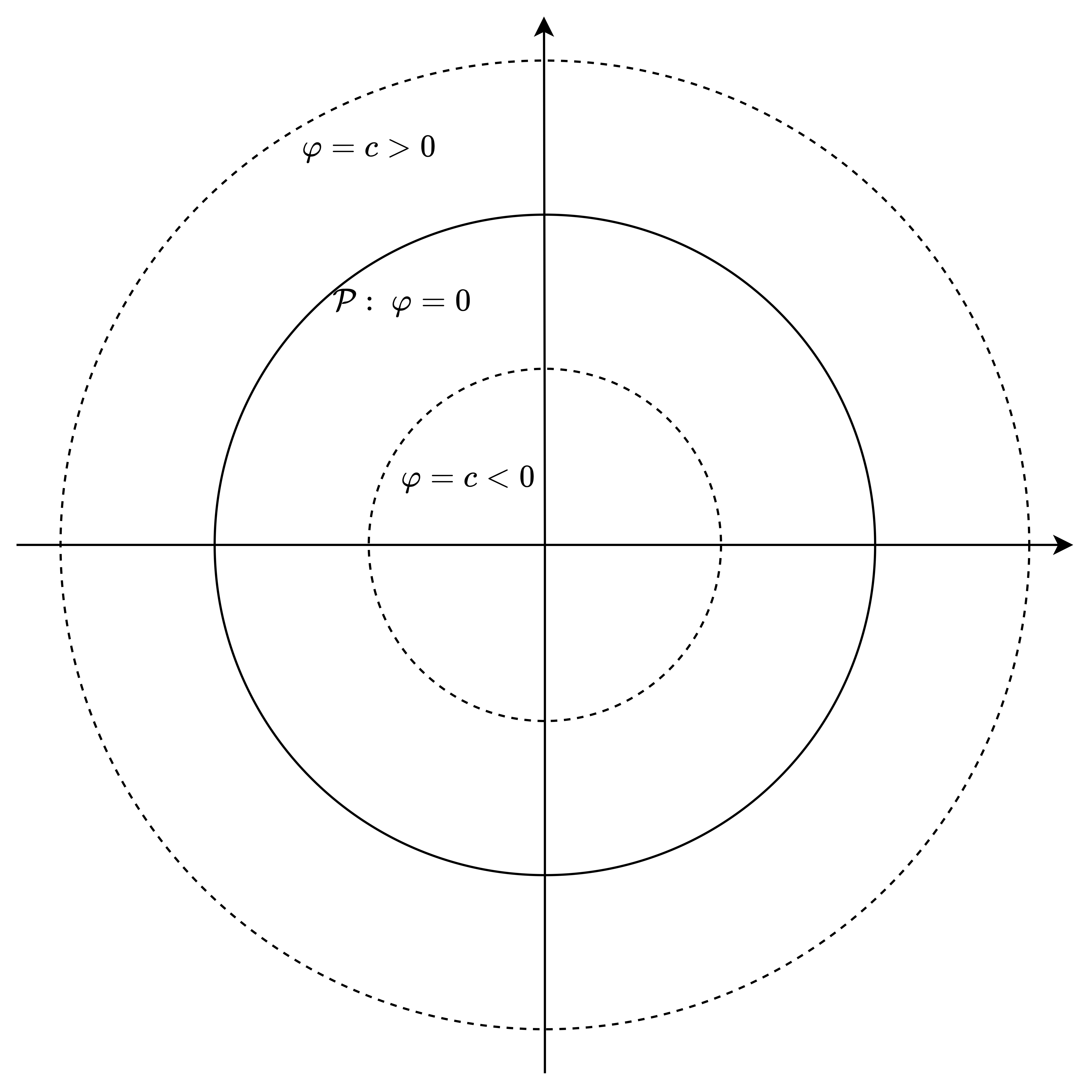
如下图所示,当
φ
=
c
=
c
o
n
s
t
\varphi=c=const
φ=c=const时,期望轨迹为一个水平集。设无人机位置坐标为
r
⃗
=
(
r
x
,
r
y
)
\vec{r}=(r_x,\ r_y)
r=(rx, ry),当
φ
(
r
⃗
)
=
0
\varphi(\vec r)=0
φ(r)=0时,无人机坐标落在期望轨迹水平集上;当
φ
(
r
⃗
)
>
0
\varphi(\vec r)>0
φ(r)>0,轨迹在期望轨迹水平集之上;当
φ
(
r
⃗
)
<
0
\varphi(\vec r)<0
φ(r)<0,轨迹在期望轨迹水平集之下。因此
φ
(
r
⃗
)
\varphi(\vec r)
φ(r)的值可以被看作是无人机位置与期望轨迹之间的距离。
通常,我们可以在此基础上定义跟踪误差为
e
=
ψ
[
φ
(
r
⃗
)
]
e=\psi[\varphi(\vec r)]
e=ψ[φ(r)]
ψ
\psi
ψ为一阶连续,单调递增函数,
ψ
(
0
)
=
0
\psi(0)=0
ψ(0)=0且
∀
z
≠
0
,
ψ
(
z
)
z
>
0
\forall z\neq0,\ \psi(z)z>0
∀z=0, ψ(z)z>0。
函数
ψ
\psi
ψ可以看作为算法的参数,通过选取
ψ
\psi
ψ和
ϕ
\phi
ϕ的自由组合,来定义跟踪误差,从而区分轨迹函数
φ
(
r
⃗
)
\varphi(\vec r)
φ(r)和
e
e
e。
导航向量场
下面给出导航向量场的形式
v
⃗
(
r
⃗
)
=
τ
⃗
(
r
⃗
)
−
k
n
e
(
r
⃗
)
n
⃗
(
r
⃗
)
\vec v(\vec r)=\vec{\tau}(\vec r)-k_ne(\vec r)\vec n(\vec r)
v(r)=τ(r)−kne(r)n(r)
式中,
n
⃗
(
r
⃗
)
\vec n(\vec r)
n(r)为梯度方向
n
⃗
(
r
⃗
)
=
(
∂
φ
∂
x
,
∂
φ
∂
y
)
=
(
x
x
2
+
y
2
,
y
x
2
+
y
2
)
\begin{aligned} \vec n(\vec r) &= (\frac{\partial \varphi}{\partial x},\frac{\partial \varphi}{\partial y}) \\ &=(\frac{x}{\sqrt{x^2+y^2}},\frac{y}{\sqrt{x^2+y^2}})\\ \end{aligned}
n(r)=(∂x∂φ,∂y∂φ)=(x2+y2x,x2+y2y)
τ
⃗
(
r
⃗
)
\vec{\tau}(\vec r)
τ(r)为与
n
⃗
(
r
⃗
)
\vec n(\vec r)
n(r)相垂直的方向,
E
E
E为旋转矩阵,
E
c
w
E_{cw}
Ecw为顺时针旋转矩阵,
E
c
c
w
E_{ccw}
Eccw为逆时针旋转矩阵
{
τ
⃗
(
r
⃗
)
=
E
n
⃗
(
r
⃗
)
E
c
w
=
[
0
1
−
1
0
]
E
c
c
w
=
[
0
−
1
1
0
]
\begin{cases} \begin{aligned} \vec{\tau}(\vec r)&= E\ \vec{n}(\vec r)\\ E_{cw}&= \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}\\ E_{ccw}&= \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \end{aligned} \end{cases}
⎩
⎨
⎧τ(r)EcwEccw=E n(r)=[0−110]=[01−10]
e
(
r
⃗
)
e(\vec r)
e(r)为误差,这里为了方便起见,令
e
(
r
⃗
)
=
φ
(
r
⃗
)
=
x
2
+
y
2
−
10
e(\vec r)=\varphi(\vec r)=\sqrt{x^2+y^2}-10
e(r)=φ(r)=x2+y2−10
k
n
k_n
kn为增益,我们暂且令
k
n
=
1
k_n = 1
kn=1。
式 v ⃗ ( r ⃗ ) = τ ⃗ ( r ⃗ ) − k n e ( r ⃗ ) n ⃗ ( r ⃗ ) \vec v(\vec r)=\vec{\tau}(\vec r)-k_ne(\vec r)\vec n(\vec r) v(r)=τ(r)−kne(r)n(r)中, τ ⃗ ( r ⃗ ) \vec{\tau}(\vec r) τ(r)为传播项, − k n e ( r ⃗ ) n ⃗ ( r ⃗ ) -k_ne(\vec r)\vec n(\vec r) −kne(r)n(r)为收敛项。 ∣ − k n e ( r ⃗ ) n ⃗ ( r ⃗ ) ∣ |-k_ne(\vec r)\vec n(\vec r)| ∣−kne(r)n(r)∣项越大,产生的向期望轨迹方向的分量越大。 τ ⃗ ( r ⃗ ) \vec{\tau}(\vec r) τ(r)决定了跟踪期望轨迹的方向。
最终将 v ⃗ ( r ⃗ ) \vec v(\vec r) v(r)进行归一化操作
m ⃗ = v ⃗ ∣ ∣ v ⃗ ∣ ∣ \vec m = \frac{\vec v}{||\vec v||} m=∣∣v∣∣v
∣ ∣ v ⃗ ∣ ∣ ||\vec v|| ∣∣v∣∣为欧几里得范数(L2范数), m ⃗ \vec m m即为导航向量场给出的期望飞行方向向量。
向量场结果
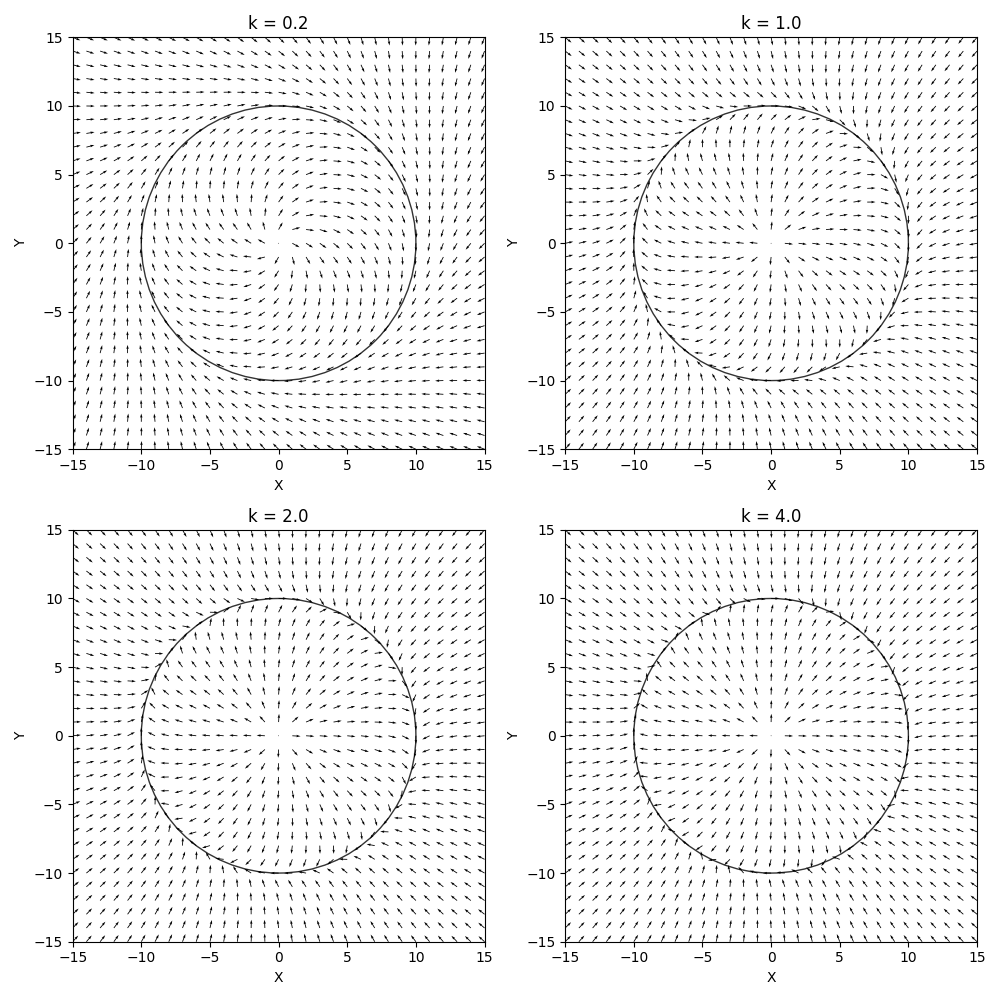
我们令增益 k n = 0.2 k_n = 0.2 kn=0.2, k n = 1 k_n = 1 kn=1, k n = 2 k_n = 2 kn=2, k n = 4 k_n = 4 kn=4,跟踪方向为顺时针方向,旋转矩阵为 E = [ 0 , 1 ; − 1 , 0 ] E=[0,1;-1,0] E=[0,1;−1,0],绘制出向量场结果图像,可得
令旋转矩阵为逆时针方向,旋转矩阵为 E = [ 0 , − 1 ; 1 , 0 ] E=[0,-1;1,0] E=[0,−1;1,0],可得
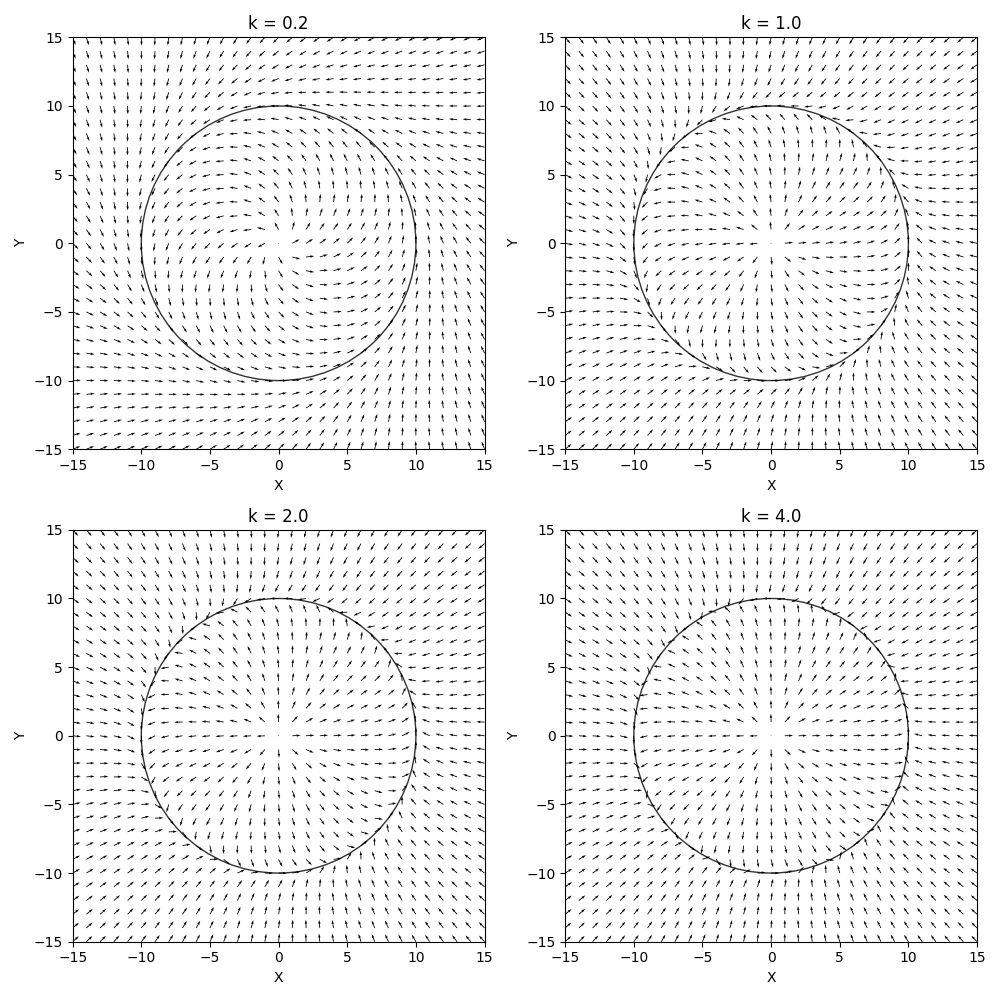
根据四个不同增益下的导航向量场结果,不难发现, ∣ − k n e ( r ⃗ ) n ⃗ ( r ⃗ ) ∣ |-k_ne(\vec r)\vec n(\vec r)| ∣−kne(r)n(r)∣项越大,导航向量场方向往期望轨迹方向偏转越大。在距离期望轨迹较近的情况下,过大的偏转方向可能会产生震荡,但是距离较远的情况下有助于快速收敛至期望轨迹。
向量场使用
根据上面的讲解,对于任意给定的期望轨迹函数式,在全局任何位置,都可以计算得出一个期望飞行向量,将向量做反正切计算,得到期望的飞行航向角。将这个期望航向角,输入至底层控制器,即可导引无人机(或其他类型机器人)飞行收敛至期望轨迹。对于固定翼无人机,不建议直接使用航向角误差作为姿态控制器的偏航输入,建议将航向角误差对滚转做映射函数处理,作为姿态控制器的滚转输入,会有更好的效果。
总结
本期文章介绍了二维导航向量场,其简洁优雅的形式,在很多方面有着比较广泛的适用性,可以自行构建轨迹函数,来实现例如目标追踪、避障、对峙跟踪等功能。
在此留下一个思考题,如有兴趣,请尝试推导出直线 x = 5 x=5 x=5和椭圆轨迹 x 2 9 + y 2 4 \frac{x^2}{9}+\frac{y^2}{4} 9x2+4y2=1的导航向量场形式,尝试绘制导航向量场结果。如果推导出结果,可以尽快与我私信,有精美礼品和源码答疑。数量有限(5个名额),先到先得。
参考文献及链接
[1]KAPITANYUK, Yuri A.; PROSKURNIKOV, Anton V.; CAO, Ming. A guiding vector-field algorithm for path-following control of nonholonomic mobile robots. IEEE Transactions on Control Systems Technology, 2017, 26.4: 1372-1385.
END
迅翼SwiftWing致力于固定翼技术共享,汇聚固定翼领域技术极客,推动固定翼技术持续创新!