ML 系列：机器学习和深度学习的深层次总结(16) — 提高 KNN 效率-使用 KD 树和球树实现更快的算法

一、说明

在机器学习系列的第 16 节，我们重点介绍了提高 K 最近邻（KNN）算法的效率，这是一种广泛用于分类和回归任务的方法。虽然 KNN 简单有效，但对于大型数据集来说，其计算成本可能会令人望而却步。为了解决这个问题，我们引入了两种高级数据结构：KD 树和球树，它们显着提高了 KNN 搜索的速度。

二、了解 KNN 的挑战

KNN 的工作原理是查找离查询点最近的数据点，并根据其标签进行预测。但是，简单方法需要计算从查询点到数据集中每个点的距离，导致每个查询的时间复杂度为 O（n），其中 n 是数据点的数量。对于大型数据集，这可能非常慢，尤其是在高维空间中。

三、KD 树：高效的空间分区

KD 树（K 维树）是一种二叉树数据结构，它以递归方式将数据空间划分为超矩形。以下是他们改进 KNN 的方法：

1. 构建：根据一个维度的中位数，在每个节点将数据集分为两半，在每个级别的维度之间循环。
2. 搜索：不是将查询点与每个数据点进行比较，而是将搜索限制在树的特定分支上，从而显著减少了距离计算的数量。

优势：KD 树对于低维到中高维数据（通常最多 20 维）非常有效。
限制：由于维度的诅咒，性能会随着维度的增加而降低。

3.1 球树：更适合高尺寸

球树解决了 KD 树的一些限制，尤其是在更高的维度中。它们使用不同的分区策略：

1. 构造：数据空间被划分为嵌套的超球体（球），每个超球体都包含一个数据点的子集。
2. 搜索：与 KD 树一样，球树通过仅关注相关区域来修剪大部分搜索空间。

优势：球树在高维空间中的性能优于 KD 树，并且可以更有效地处理非均匀数据分布。
限制：它们通常比 KD 树更复杂地实现和维护。

3.2 在实践中实现 KD 树和球树

KD 树和球树在流行的机器学习库（如 scikit-learn）中都受支持。以下是如何在 scikit-learn 中使用这些结构实现 KNN 的简短示例：

from sklearn.neighbors import KNeighborsClassifier
# Using KD-tree
knn_kd = KNeighborsClassifier(algorithm='kd_tree')
knn_kd.fit(X_train, y_train)
predictions_kd = knn_kd.predict(X_test)
# Using Ball Tree
knn_ball = KNeighborsClassifier(algorithm='ball_tree')
knn_ball.fit(X_train, y_train)
predictions_ball = knn_ball.predict(X_test)

四、KD树的原理

4.1 什么是K维树？

KD 树（也称为 K 维树）是一种二叉搜索树，其中每个节点中的数据是空间中的 K 维点。简而言之，它是一种空间分区（详情如下）数据结构，用于组织 K 维空间中的点。KD 树中的非叶节点将空间分为两部分，称为半空间。该空间左侧的点由该节点的左子树表示，空间右侧的点由右子树表示。我们很快就会解释如何划分空间和形成树的概念。为简单起见，让我们通过一个例子来理解 2-D 树。根将有一个 x 对齐的平面，根的子节点都将具有 y 对齐的平面，根的孙子节点都将具有 x 对齐的平面，根的曾孙节点都将具有 y 对齐的平面，依此类推。

概括：我们将平面编号为 0、1、2、…（K – 1）。从上面的例子中可以清楚地看出，深度为 D 的点（节点）将具有 A 对齐平面，其中 A 的计算方式为：A = D mod K

如何确定一个点位于左子树还是右子树？如果根节点在平面 A 中对齐，则左子树将包含该平面中坐标小于根节点的所有点。同样，右子树将包含该平面中坐标大于或等于根节点的所有点。

创建二维树：考虑二维平面中的以下点：(3, 6)、(17, 15)、(13, 15)、(6, 12)、(9, 1)、(2, 7)、(10, 19)

插入（3，6）：由于树为空，因此将其作为根节点。
插入（17，15）：将其与根节点点进行比较。由于根节点是 X 对齐的，因此将比较 X 坐标值以确定它位于右子树还是左子树中。该点将 Y 对齐。
插入 (13, 15)：此点的 X 值大于根节点中点的 X 值。因此，这将位于 (3, 6) 的右子树中。再次将此点的 Y 值与点 (17, 15) 的 Y 值进行比较（为什么？）。由于它们相等，因此该点将位于 (17, 15) 的右子树中。该点将 X 对齐。
插入 (6, 12)：此点的 X 值大于根节点中点的 X 值。因此，这将位于 (3, 6) 的右子树中。再次将此点的 Y 值与点 (17, 15) 的 Y 值进行比较（为什么？）。由于 12 < 15，因此此点将位于 (17, 15) 的左子树中。此点将 X 对齐。
插入(9, 1):同样，该点将位于(6, 12)的右边。
插入(2, 7)：同样，该点将位于(3, 6)的左边。
插入（10,19）：同样，该点将位于（13,15）的左边。

ktree_1

空间是如何划分的？

所有 7 个点都将在 XY 平面上绘制如下：

点（3, 6）将空间分成两部分：画线 X = 3。
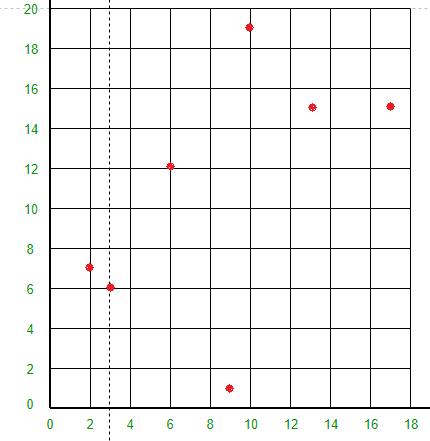
点 (2, 7) 将线 X = 3 左侧的空间水平分成两部分。在线 X = 3 左侧绘制线 Y = 7。
点 (17, 15) 将线 X = 3 右侧的空间水平分成两部分。在线 X = 3 右侧绘制线 Y = 15。
点 (6, 12) 将线 Y = 15 下方和线 X = 3 右侧的空间分成两部分。将线 X = 6 绘制在线 X = 3 的右侧和线 Y = 15 下方。
点 (13, 15) 将线 Y = 15 下方和线 X = 6 右侧的空间分成两部分。将线 X = 13 绘制在线 X = 6 的右侧和线 Y = 15 下方。
点 (9, 1) 将线 X = 3、X = 6 和 Y = 15 之间的空间分成两部分。在线 X = 3 和 X = 13 之间绘制线 Y = 1。
点 (10, 19) 将线 X = 3 右侧和线 Y = 15 上方的空间分成两部分。将线 Y = 19 绘制在线 X = 3 右侧和线 Y = 15 上方。

以下是 KD 树基本操作（如搜索、插入和删除）的 C++ 实现。

C++
Java
Python3
C#
JavaScript

// A C++ program to demonstrate operations of KD tree

#include<bits/stdc++.h>

using namespace std;

const int k = 2;

// A structure to represent node of kd tree

struct Node

{

int point[k]; // To store k dimensional point

Node *left, *right;

};

// A method to create a node of K D tree

struct Node* newNode(int arr[])

{

struct Node* temp = new Node;

for (int i=0; i<k; i++)

temp->point[i] = arr[i];

temp->left = temp->right = NULL;

return temp;

}

// Inserts a new node and returns root of modified tree

// The parameter depth is used to decide axis of comparison

Node *insertRec(Node *root, int point[], unsigned depth)

{

// Tree is empty?

if (root == NULL)

return newNode(point);

// Calculate current dimension (cd) of comparison

unsigned cd = depth % k;

// Compare the new point with root on current dimension 'cd'

// and decide the left or right subtree

if (point[cd] < (root->point[cd]))

root->left = insertRec(root->left, point, depth + 1);

else

root->right = insertRec(root->right, point, depth + 1);

return root;

}

// Function to insert a new point with given point in

// KD Tree and return new root. It mainly uses above recursive

// function "insertRec()"

Node* insert(Node *root, int point[])

{

return insertRec(root, point, 0);

}

// A utility method to determine if two Points are same

// in K Dimensional space

bool arePointsSame(int point1[], int point2[])

{

// Compare individual pointinate values

for (int i = 0; i < k; ++i)

if (point1[i] != point2[i])

return false;

return true;

}

// Searches a Point represented by "point[]" in the K D tree.

// The parameter depth is used to determine current axis.

bool searchRec(Node* root, int point[], unsigned depth)

{

// Base cases

if (root == NULL)

return false;

if (arePointsSame(root->point, point))

return true;

// Current dimension is computed using current depth and total

// dimensions (k)

unsigned cd = depth % k;

// Compare point with root with respect to cd (Current dimension)

if (point[cd] < root->point[cd])

return searchRec(root->left, point, depth + 1);

return searchRec(root->right, point, depth + 1);

}

// Searches a Point in the K D tree. It mainly uses

// searchRec()

bool search(Node* root, int point[])

{

// Pass current depth as 0

return searchRec(root, point, 0);

}

// Driver program to test above functions

int main()

{

struct Node *root = NULL;

int points[][k] = {{3, 6}, {17, 15}, {13, 15}, {6, 12},

{9, 1}, {2, 7}, {10, 19}};

int n = sizeof(points)/sizeof(points[0]);

for (int i=0; i<n; i++)

root = insert(root, points[i]);

int point1[] = {10, 19};

(search(root, point1))? cout << "Found\n": cout << "Not Found\n";

int point2[] = {12, 19};

(search(root, point2))? cout << "Found\n": cout << "Not Found\n";

return 0;

}

输出：

成立
未找到

时间复杂度：O（n）
辅助空间：O（n）

请参阅以下文章以了解如何查找最小值和删除操作。

KD 树 (查找最小值)
KD 树（删除）

4.2 K维树的优点-

Kd树作为一种数据结构有几个优点：

高效搜索：Kd 树可有效搜索 k 维空间中的点，例如最近邻搜索或范围搜索。
降维： Kd 树可用于降低问题的维数，从而缩短搜索时间并减少数据结构的内存要求。
多功能性： Kd树可用于广泛的应用，例如数据挖掘、计算机图形学和科学计算。
平衡： Kd 树是自平衡的，这确保了即使插入或删除数据时树仍然保持高效。
增量构建： Kd 树可以增量构建，这意味着可以在结构中添加或删除数据，而不必重建整个树。
易于实现： Kd树相对容易实现，可以用多种编程语言来实现。

参考题目：

Search and Insertion in K Dimensional tree - GeeksforGeeks