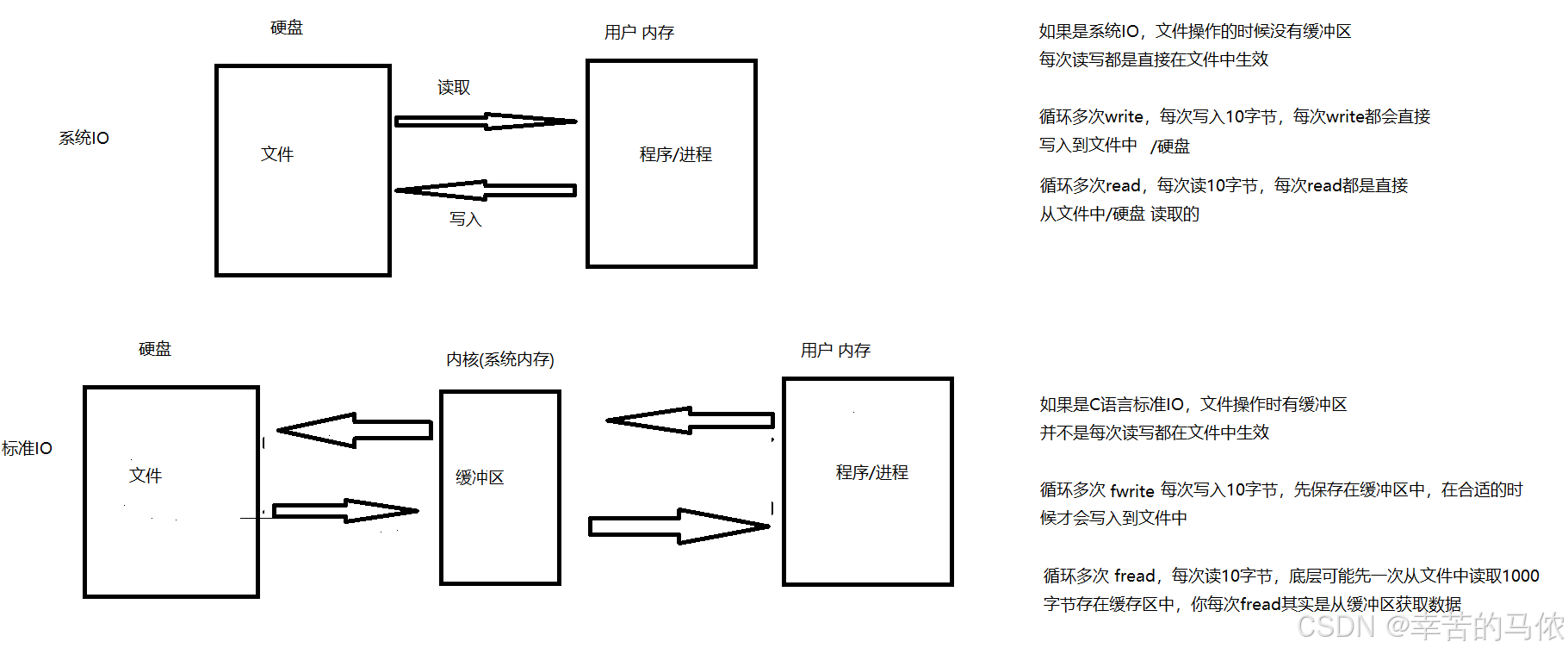
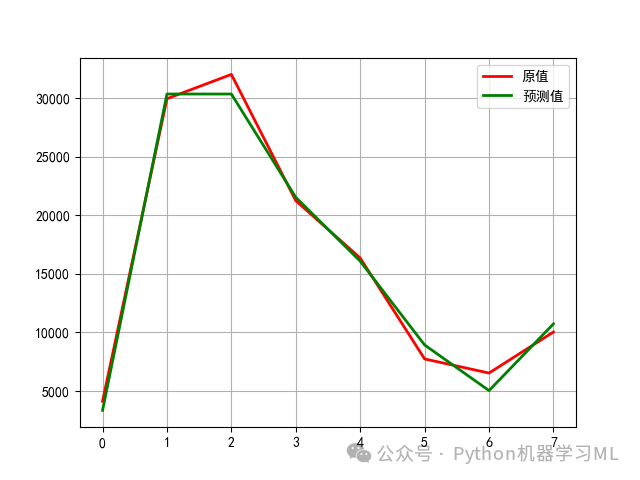
本文只适用于闭合多段线组成的图像,其他情况(圆、弧、椭圆、未封闭line)暂不支持。
效果如下图所示:

原始图:

代码运行后图:

附代码:
public class 外轮廓
{
Database db = HostApplicationServices.WorkingDatabase;
[CommandMethod("xx")]
public void Demo()
{
try
{
//ObjectId obj = db.GetCenterPl();
// return;
// List<DBText> dbtext = db.SelectEntities<DBText>();
// return;
// db.GetEntities(out List<Curve> curve, "aa");
// return;
if (!db.GetEntities(out List<Curve> curve, "框选识别外轮廓的图像"))
return;
List<Line> lines = new List<Line>();
foreach (var item in curve)
{
if (item is Line) lines.Add(item as Line);


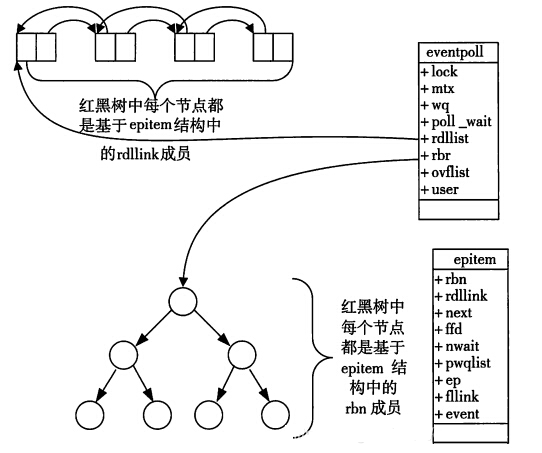









![【题解】【模拟】—— [NOIP2013 普及组] 表达式求值](https://i-blog.csdnimg.cn/direct/f782c1acde024adb925001c00e7952f4.jpeg#pic_center)